8. Sisteme de Coordonate de Referință

	Obiective:	Să înțelegem Sistemele de Coordonate de Referință
	Cuvinte cheie:	Sistemul de coordonate de referință (CRS), Proiecția Hărții, Proiecția „din zbor”, Latitudinea, Longitudinea, Nord, Est

8.1. Prezentare generală

Map projections try to portray the surface of the earth, or a portion of the earth, on a flat piece of paper or computer screen. In layman’s term, map projections try to transform the earth from its spherical shape (3D) to a planar shape (2D).

A coordinate reference system (CRS) then defines how the two-dimensional, projected map in your GIS relates to real places on the earth. The decision of which map projection and CRS to use depends on the regional extent of the area you want to work in, on the analysis you want to do, and often on the availability of data.

8.2. Proiecția hărții în detaliu

O metodă tradițională de a reprezenta forma Pământului este utilizarea globurilor. Există, totuși, o problemă cu această abordare. Deși globurile au, în general, forma Pământului și ilustrează configurația spațială a entităților de mărimea unui continent, ele sunt foarte greu de cărat în buzunarul cuiva. Acestea sunt, de asemenea, convenabil de utilizat la scări extrem de mici (de exemplu, 1:100 de milioane).

Cele mai multe dintre datele hărților tematice, frecvent utilizate în aplicațiile GIS, au o scară mult mai mare. Seturile de date GIS tipice au scări de 1: 250 000 sau mai mult, în funcție de nivelul de detaliere. Un glob de această dimensiune ar fi dificil și costisitor de produs, și chiar mult mai dificil de transportat. Ca rezultat, cartografii au dezvoltat un set de tehnici denumite proiecții de hartă, concepute pentru a afișa în două dimensiuni, cu o precizie rezonabilă, pământul sferic.

Atunci când este privit de aproape, pământul pare să fie relativ plat. Cu toate acestea, atunci când este privit din spațiu, putem vedea că pământul este relativ sferic. Hărțile, așa cum vom vedea în viitorul subiect de producție a hărților, sunt reprezentări ale realității. Acestea sunt concepute pentru a reprezenta nu numai entități, ci, de asemenea, forma și aranjarea lor în spațiu. Fiecare proiecție de hartă are atât avantaje cât și dezavantaje. Cea mai bună proiecție pentru o hartă depinde de scara hărții, și de scopurile în care va fi utilizată. De exemplu, o proiecție poate avea distorsiuni inacceptabile dacă este folosit pentru a cartografia întreg continentul african, dar poate fi o alegere excelentă pentru o hartă la scară largă (detaliată) a țării dumneavoastră. Proprietățile unei proiecții de hartă pot influența unele dintre funcțiile de proiectare ale hărții. Unele proiecții sunt bune pentru zonele mici, altele sunt bune pentru cartografierea zonelor cu o mare extindere pe direcția Est-Vest, iar altele sunt mai bune pentru cartografierea zonelor cu o mare extindere pe direcția Nord-Sud.

8.3. Cele trei familii ale proiecțiilor hărții

The process of creating map projections is best illustrated by positioning a light source inside a transparent globe on which opaque earth features are placed. Then project the feature outlines onto a two-dimensional flat piece of paper. Different ways of projecting can be produced by surrounding the globe in a cylindrical fashion, as a cone, or even as a flat surface. Each of these methods produces what is called a map projection family. Therefore, there is a family of planar projections, a family of cylindrical projections, and another called conical projections (see Fig. 8.3)

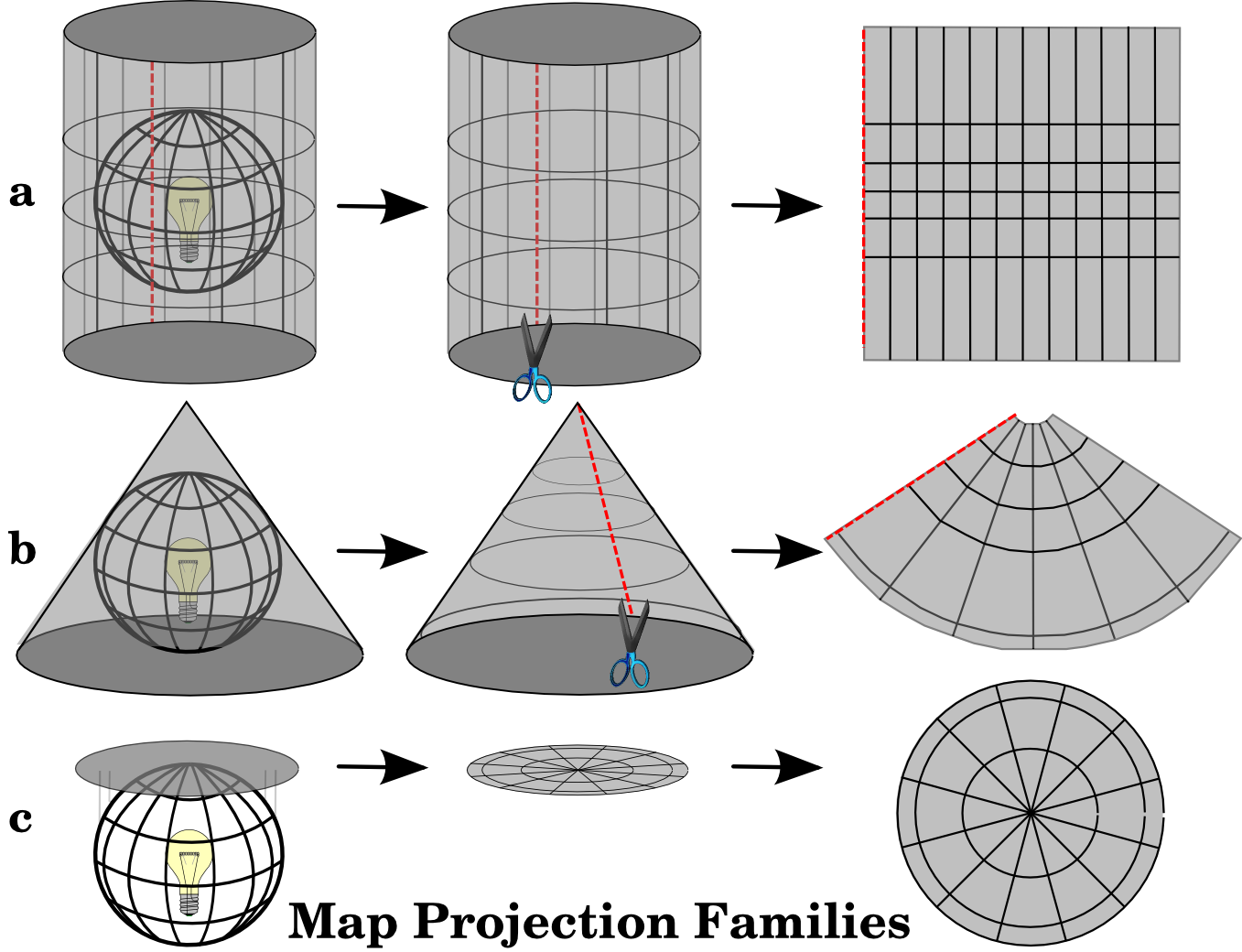
Fig. 8.3 Cele trei familii de proiecții pentru hărți. Acestea sunt reprezentate de proiecțiile a) cilindrice, b) conice sau c) planare.

Astăzi, desigur, procesul de proiectare a pământului sferic pe o bucată de hârtie plată, se face folosind principiile matematice ale geometriei și trigonometriei. Aceasta recreează proiecția fizică a luminii printr-un glob.

8.4. Acuratețea proiecțiilor hărții

Proiecțiile de hartă nu sunt reprezentări absolut precise ale pământului sferic. Ca rezultat al procesului de proiecție, fiecare hartă prezintă distorsiuni de conformitate unghiulară, distanță și arie. O proiecție de hartă poate avea doar unele dintre aceste caracteristici, sau poate reprezenta un compromis care denaturează, în limite acceptabile, toate proprietățile unei zone, distanța și conformitatea unghiulară. Două exemple de compromis de proiecție sunt Proiecția Triplă Winkel și Proiecția Robinson (a se vedea Fig. 8.4), care sunt adesea folosite pentru vizualizarea hărții globului.

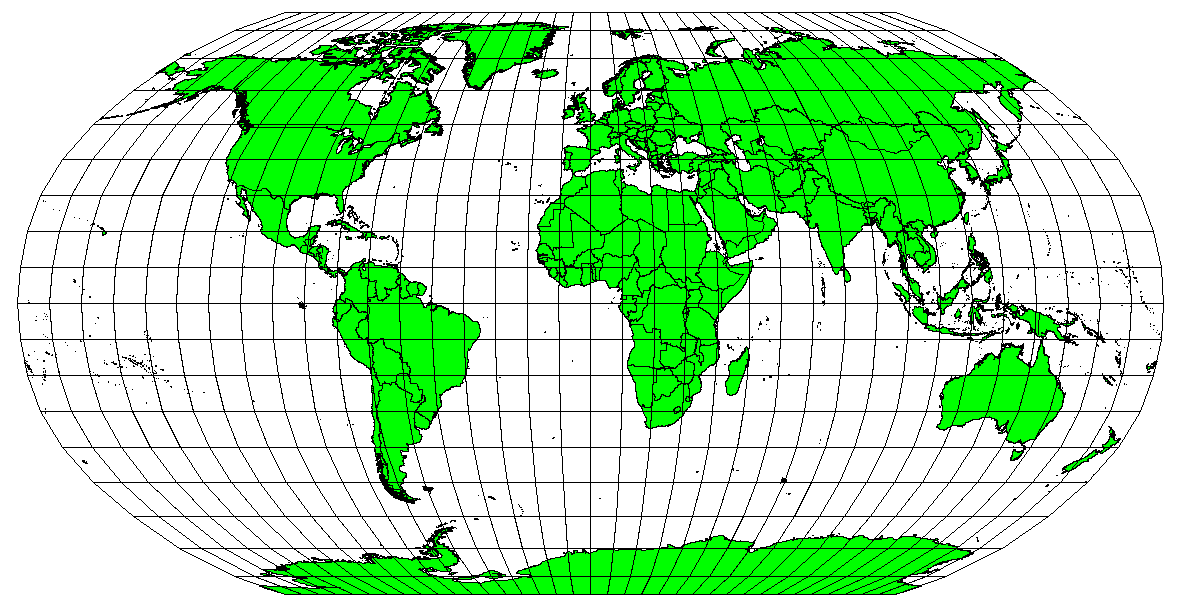
Fig. 8.4 Proiecția Robinson reprezintă un compromis în care distorsionarea suprafețelor, conformitatea unghiurilor și a distanțelor sunt acceptabile.

De obicei, este imposibil să păstrăm simultan toate caracteristicile unei proiecții de hartă. Acest lucru înseamnă că, atunci când doriți să efectuați operațiuni de analiză precise, trebuie să utilizați o proiecție de hartă care oferă cele mai bune caracteristici pentru analize. De exemplu, dacă aveți nevoie de măsurarea distanțelor pe hartă, ar trebui să încercați să utilizați o proiecție de hartă care cooferă mai multă precizie distanțelor.

8.4.1. Proiecții de hartă cu conformitate unghiulară

Atunci când se lucrează cu un glob, principalele direcții ale busolei (Nord, Est, Sud și Vest) se vor afla întotdeauna la 90 de grade una față de cealaltă. Cu alte cuvinte, Estul va fi situat întotdeauna la un unghi de 90 de grade față de nord. De asemenea, menținerea proprietăților unghiulare corecte pot fi păstrate și pe o proiecție a hărții. O proiecție a hărții care păstrează această proprietate de conformitate unghiulară se numește conformă sau ortomorfică.

Aceste proiecții sunt utilizate atunci când păstrarea relațiilor unghiulare este importantă. Ele sunt frecvent utilizate pentru activități de navigație sau meteorologice. Este important să ne amintim că menținerea unghiurilor reale pe o hartă este dificilă pentru suprafețe mari, acest lucru trebuind să fie încercat doar pentru porțiuni mici de pe sol. Tipul conform de proiecție duce la denaturarea zonei, ceea ce înseamnă că în cazul în care măsurătorile sunt efectuate pe hartă, ele vor fi incorecte. Cu cât mai mare este zona, cu atât mai puțin precise vor fi măsurătorile suprafeței. Exemple sunt Proiecția Mercator (așa cum se arată în Fig. 8.5) și Proiecția Conică Conformă Lambert. US Geological Survey folosește o proiecție conformă pentru majoritatea hărților sale topografice.

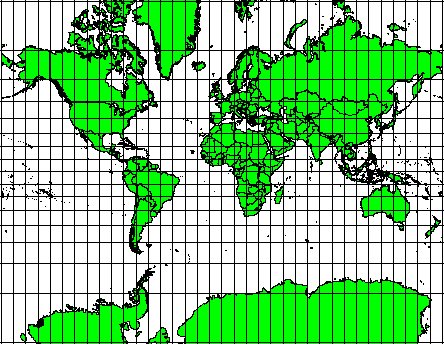
Fig. 8.5 Proiecția Mercator, de exemplu, se utilizează pentru cazurile în care sunt importante relațiile unghiulare, relațiile dintre suprafețe fiind totuși distorsionate.

8.4.2. Proiecții de hartă cu distanță egală

Dacă obiectivul dvs., la proiectarea unei hărți, este de a măsura cu precizie distanțele, trebuie să selectați o proiecție care este indicată pentru a păstra bine distanțele. Astfel de proiecții, denumite echidistante, necesită ca scara hărții să fie menținută constantă. O hartă este echidistantă atunci când reprezintă corect distanțele de la centrul de proiecție înspre orice alt loc de pe hartă. Proiecțiile echidistante mențin distanțele exacte din centrul proiecției, sau pe cele aflate de-a lungul liniilor date. Aceste proiecții sunt utilizate pentru cartografiere radio și seismică, și pentru navigare. Plate Carree Equidistant Cylindrical (a se vedea Fig. 8.6) și Proiecția echirectangulară sunt două exemple bune de proiecții echidistante. Proiecția Echidistantă Azimutală este proiecția folosită la crearea emblemei Organizației Națiunilor Unite (a se vedea Fig. 8.7).

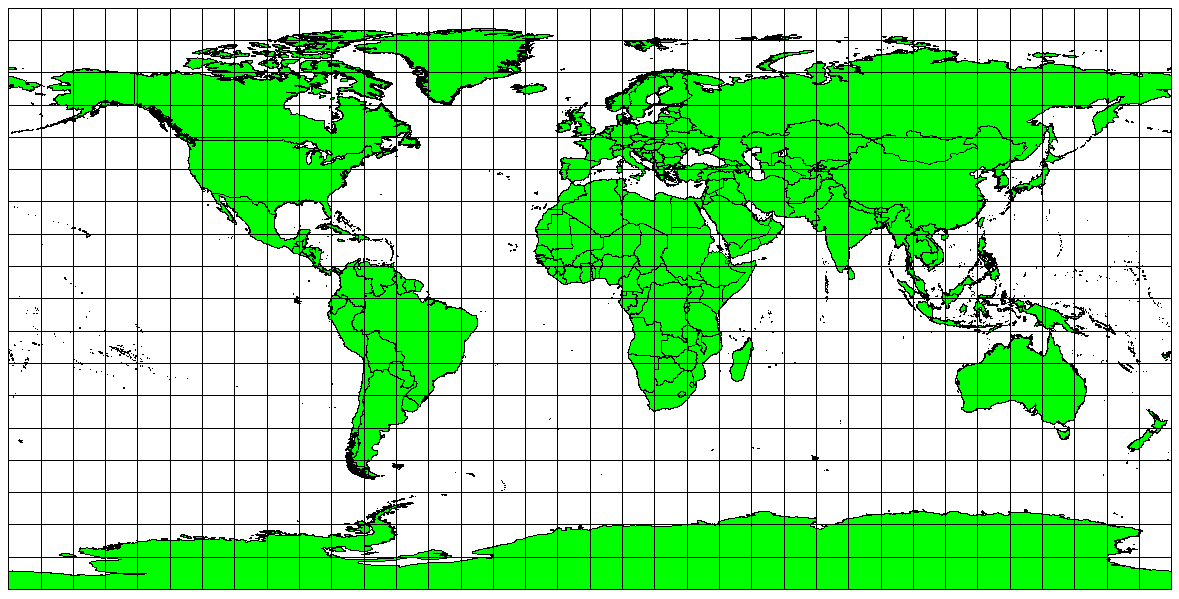
Fig. 8.6 Proiecția Plate Carree Equidistant Cylindrical, de exemplu, se utilizează atunci când este importantă măsurarea distanței exacte.

Fig. 8.7 Logo-ul Națiunilor Unite folosește proiecția Echidistantă Azimutală.

8.4.3. Proiecții cu arii egale

When a map portrays areas over the entire map, so that all mapped areas have the same proportional relationship to the areas on the Earth that they represent, the map is an equal area map. In practice, general reference and educational maps most often require the use of equal area projections. As the name implies, these maps are best used when calculations of area are the dominant calculations you will perform. If, for example, you are trying to analyse a particular area in your town to find out whether it is large enough for a new shopping mall, equal area projections are the best choice. On the one hand, the larger the area you are analysing, the more precise your area measures will be, if you use an equal area projection rather than another type. On the other hand, an equal area projection results in distortions of angular conformity when dealing with large areas. Small areas will be far less prone to having their angles distorted when you use an equal area projection. Alber’s equal area, Lambert’s equal area and Mollweide Equal Area Cylindrical projections (shown in Fig. 8.8) are types of equal area projections that are often encountered in GIS work.

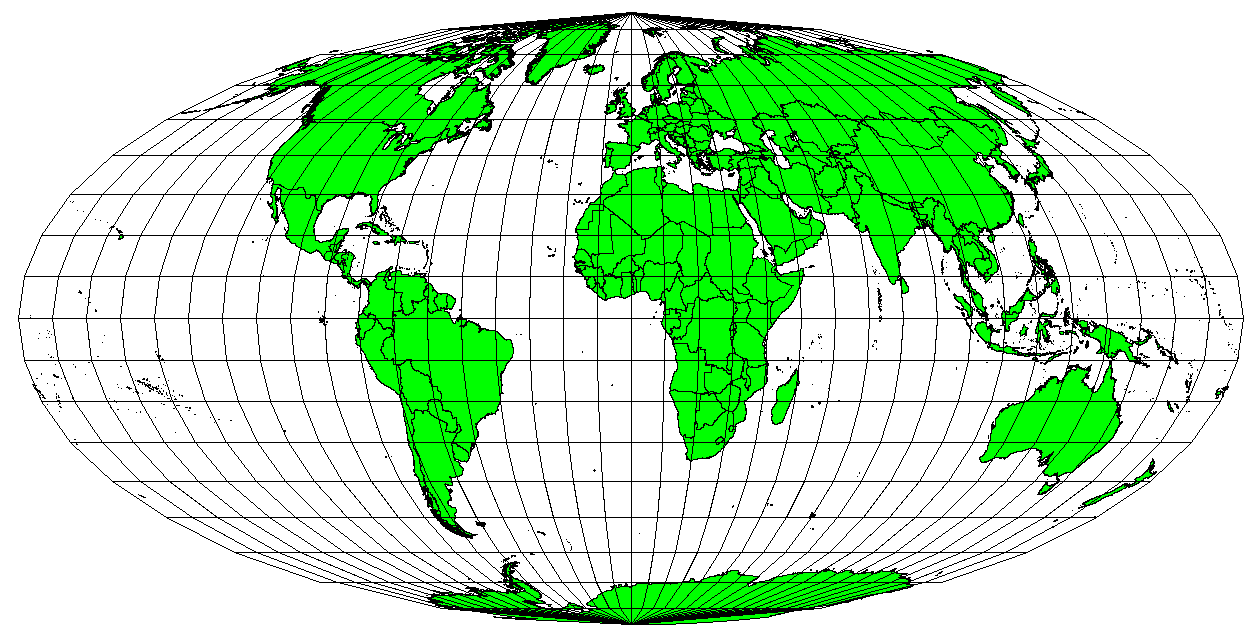
Fig. 8.8 Proiecția Mollweide Equal Area Cylindrical, de exemplu, garantează că toate zonele mapate păstrează aceeași relație proporțională pentru toate suprafețele terestre.

Rețineți că proiecția hărții este un subiect foarte complex. Există sute de proiecții diferite, disponibile global, fiecare încercând să prezinte, pe o bucată de hârtie plată, o anumită parte din suprafața pământului, cât mai fidel posibil. În realitate, alegerea proiecției care se va utiliza, va rămâne în sarcina dvs. Cele mai multe țări folosesc proiecții comune, iar atunci când datele sunt transmise altor persoane, acestea vor urma trendul național.

8.5. Sistemul de coordonate de referinţă (CRS) în detaliu

Cu ajutorul Sistemelor de Coordonate de Referință (CRS) fiecare loc de pe pământ poate fi specificat printr-un set de trei numere, numite coordonate. În general, CRS-urile pot fi împărțite în Sisteme de Coordonate de Referință Proiectate (de asemenea, denumite sisteme de coordonate de referință carteziene sau dreptunghiulare) și Sisteme de Coordonate de Referință Geografice.

8.5.1. Sisteme de coordonate geografice

Folosirea Sistemelor de Coordonate de Referință Geografice este foarte frecventă. Ele folosesc grade de latitudine și longitudine și, uneori, o valoare pentru înălțime, pentru a descrie o locație de pe suprafața pământului. Cel mai populare este denumit WGS 84.

Lines of latitude run parallel to the equator and divide the earth into 180 equally spaced sections from North to South (or South to North). The reference line for latitude is the equator and each hemisphere is divided into ninety sections, each representing one degree of latitude. In the northern hemisphere, degrees of latitude are measured from zero at the equator to ninety at the north pole. In the southern hemisphere, degrees of latitude are measured from zero at the equator to ninety degrees at the south pole. To simplify the digitisation of maps, degrees of latitude in the southern hemisphere are often assigned negative values (0 to -90°). Wherever you are on the earth’s surface, the distance between the lines of latitude is the same (60 nautical miles). See Fig. 8.9 for a pictorial view.

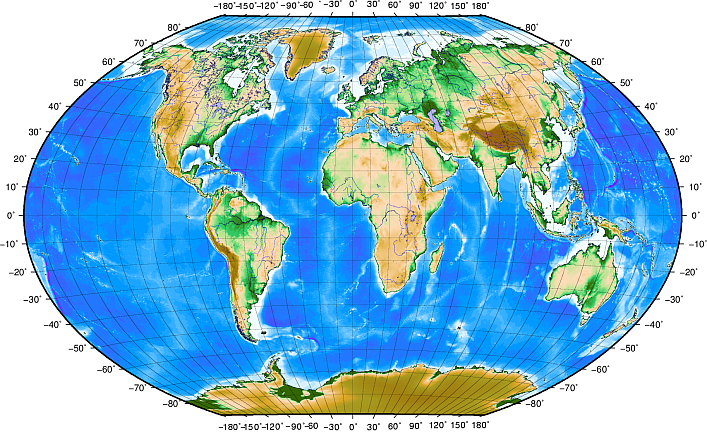
Fig. 8.9 Așezare geografică cu linii de latitudine paralele cu ecuatorul, și linii de longitudine cu primul meridian trecând prin Greenwich.

Lines of longitude, on the other hand, do not stand up so well to the standard of uniformity. Lines of longitude run perpendicular to the equator and converge at the poles. The reference line for longitude (the prime meridian) runs from the North pole to the South pole through Greenwich, England. Subsequent lines of longitude are measured from zero to 180 degrees East or West of the prime meridian. Note that values West of the prime meridian are assigned negative values for use in digital mapping applications. See Fig. 8.9 for a pictorial view.

La ecuator, și numai la ecuator, distanța reprezentată de o linie de longitudine este egală cu distanța reprezentată de un grad de latitudine. Pe măsură ce ne îndreptăm spre poli, distanța dintre liniile de longitudine devine progresiv mai mică, până când, la locația exactă a polului, toate cele 360° de longitudine sunt reprezentate printr-un singur punct care se poate atinge cu degetul (probabil că ar trebui să purtați mănuși, totuși). Sistemele de coordonate geografice folosesc o grilă cu linii de divizare a pământului în caroiaje, care acoperă aproximativ 12363.365 km pătrați la ecuator — un început bun, dar nu foarte util pentru determinarea amplasamentului unui reper în interiorul acestui perimetru.

Pentru a fi cu adevărat utilă, grila unei hărți trebuie să fie împărțită în secțiuni suficient de mici, astfel încât acestea să poată fi utilizate pentru a descrie (cu un nivel acceptabil de acuratețe) amplasarea unui punct de pe hartă. Pentru a realiza acest lucru, gradele sunt împărțite în minute (') și secunde ("). Într-un grad sunt șaizeci de minute, iar într-un minut sunt șaizeci de secunde (3600 secunde într-un grad). Deci, la ecuator, o secundă de latitudine sau longitudine = 30.87624 metri.

8.5.2. Sisteme de Coordonate de Referință Proiectate

A two-dimensional coordinate reference system is commonly defined by two axes. At right angles to each other, they form a so called XY-plane (see Fig. 8.10 on the left side). The horizontal axis is normally labelled X, and the vertical axis is normally labelled Y. In a three-dimensional coordinate reference system, another axis, normally labelled Z, is added. It is also at right angles to the X and Y axes. The Z axis provides the third dimension of space (see Fig. 8.10 on the right side). Every point that is expressed in spherical coordinates can be expressed as an X Y Z coordinate.

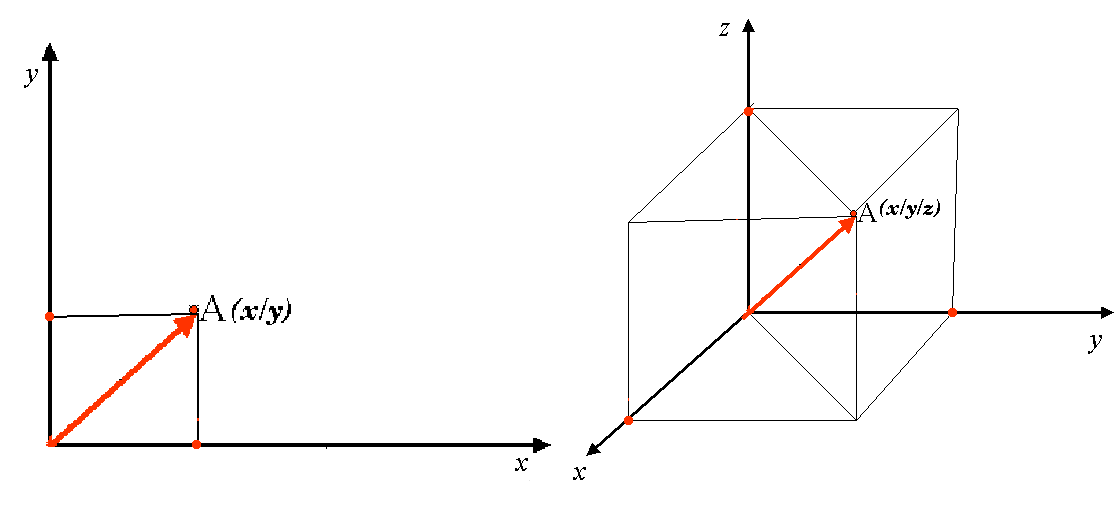
Fig. 8.10 Sisteme de coordonate de referinţă cu două și cu trei dimensiuni.

Un sistem de coordonate de referință proiectat în emisfera sudică (la sud de ecuator) are, în mod normal, originea pe ecuator, la o anumită Longitudine. Acest lucru înseamnă că valorile-Y cresc înspre sud, iar valorile-X înspre vest. În emisfera nordică (la nord de Ecuator) originea este, de asemenea pe ecuator, la o anumită Longitudine. Cu toate acestea, acum valorile-Y cresc înspre nord, iar valorile-X înspre est. În secțiunea următoare, vom descrie un sistem de coordonate de referință proiectat, numit Universal Transverse Mercator (UTM), folosit adesea pentru Africa de Sud.

8.6. CRS-ul Universal Transverse Mercator (UTM) în detaliu

The Universal Transverse Mercator (UTM) coordinate reference system has its origin on the equator at a specific Longitude. Now the Y-values increase southwards and the X-values increase to the West. The UTM CRS is a global map projection. This means, it is generally used all over the world. But as already described in the section «accuracy of map projections» above, the larger the area (for example South Africa) the more distortion of angular conformity, distance and area occur. To avoid too much distortion, the world is divided into 60 equal zones that are all 6 degrees wide in longitude from East to West. The UTM zones are numbered 1 to 60, starting at the antimeridian (zone 1 at 180 degrees West longitude) and progressing East back to the antemeridian (zone 60 at 180 degrees East longitude) as shown in Fig. 8.11.

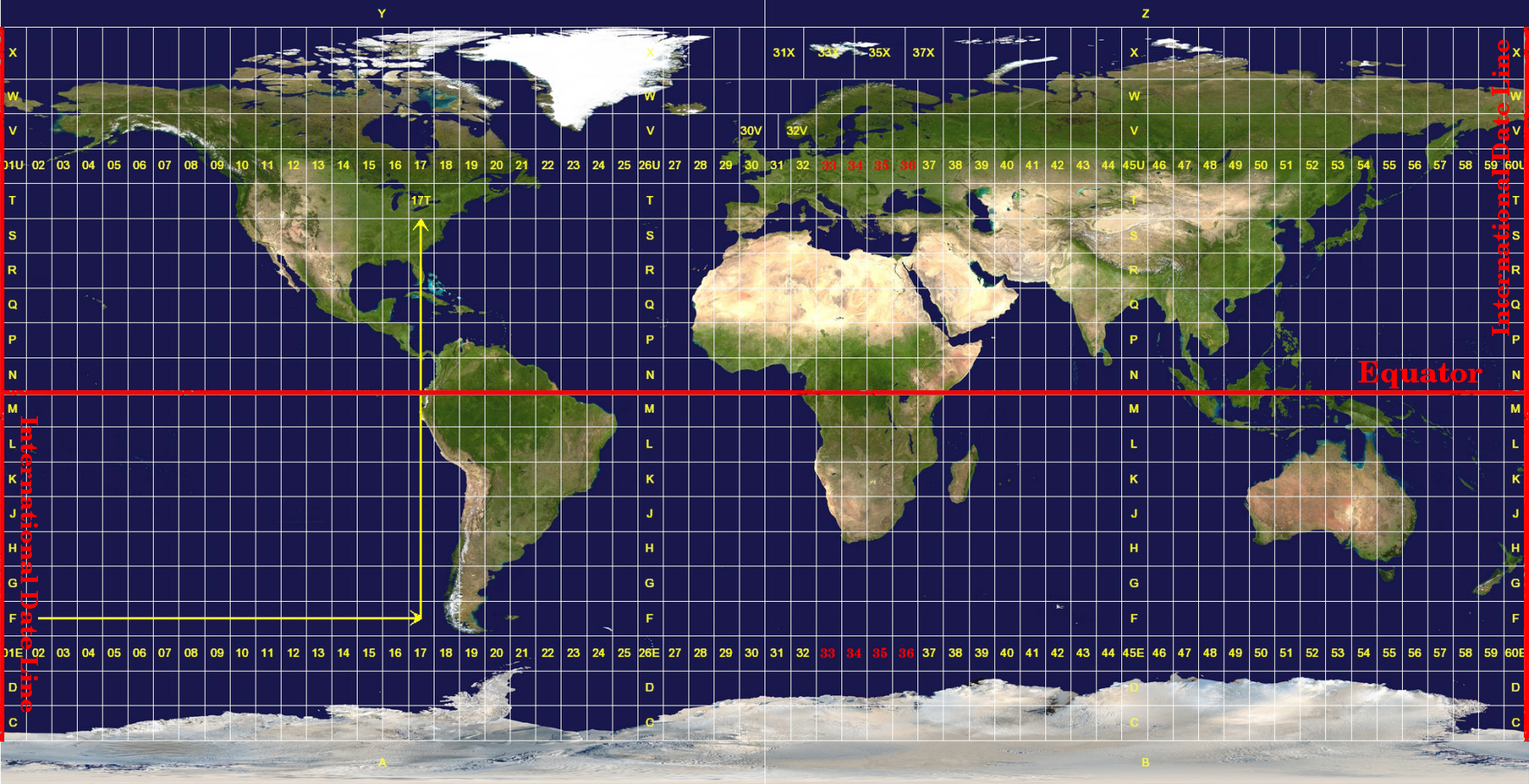
Fig. 8.11 Zonele Universal Transverse Mercator. Pentru Africa de Sud se folosesc zonele UTM 33S, 34S, 35S și 36S.

As you can see in Fig. 8.11 and Fig. 8.12, South Africa is covered by four UTM zones to minimize distortion. The zones are called UTM 33S, UTM 34S, UTM 35S and UTM 36S. The S after the zone means that the UTM zones are located south of the equator.

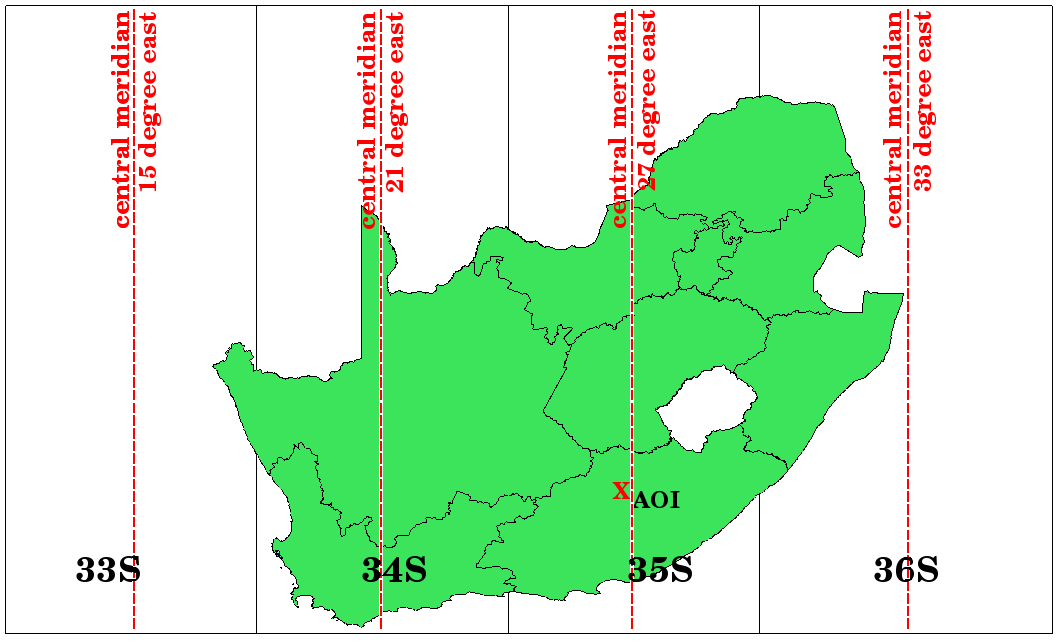
Fig. 8.12 Zonele UTM 33S, 34s, 35s, și 36S cu longitudinile lor centrale (meridianele) sunt folosite pentru a proiecta, cu mare precizie, Africa de Sud. Cruciulița roșie indică o zonă de interes (AOI).

Say, for example, that we want to define a two-dimensional coordinate within the Area of Interest (AOI) marked with a red cross in Fig. 8.12. You can see, that the area is located within the UTM zone 35S. This means, to minimize distortion and to get accurate analysis results, we should use UTM zone 35S as the coordinate reference system.

The position of a coordinate in UTM south of the equator must be indicated with the zone number (35) and with its northing (Y) value and easting (X) value in meters. The northing value is the distance of the position from the equator in meters. The easting value is the distance from the central meridian (longitude) of the used UTM zone. For UTM zone 35S it is 27 degrees East as shown in Fig. 8.12. Furthermore, because we are south of the equator and negative values are not allowed in the UTM coordinate reference system, we have to add a so called false northing value of 10,000,000 m to the northing (Y) value and a false easting value of 500,000 m to the easting (X) value. This sounds difficult, so, we will do an example that shows you how to find the correct UTM 35S coordinate for the Area of Interest.

8.6.1. Valoarea nordică (Y)

Locul pe care îl căutăm este situat la 3.550.000 metri la sud față de ecuator, astfel încât valoarea nordică (Y) va căpăta un semn negativ, ea devenind -3.550.000 m. În conformitate cu definițiile UTM trebuie să adăugați o valoare de nord fals de 10.000.000 m. Acest lucru înseamnă că valoarea nordică (Y) a coordonatei noastre este 6.450.000 m (-3.550.000 m + 10.000.000 m).

8.6.2. Valoarea estică (X)

First we have to find the central meridian (longitude) for the UTM zone 35S. As we can see in Fig. 8.12 it is 27 degrees East. The place we are looking for is 85,000 meters West from the central meridian. Just like the northing value, the easting (X) value gets a negative sign, giving a result of -85,000 m. According to the UTM definitions we have to add a false easting value of 500,000 m. This means the easting (X) value of our coordinate is 415,000 m (-85,000 m + 500,000 m). Finally, we have to add the zone number to the easting value to get the correct value.

Drept urmare, coordonatele Punctul Nostru de Interes **, proiectat în **zona UTM 35S ar trebui să fie scrise ca fiind: 35.415.000 m E / 6.450.000 m N. În unele aplicații GIS, atunci când zona UTM 35S este corect definită iar unitățile sunt setate în metri, conform sistemului, coordonatele ar putea apărea sub forma 415.000 6.450.000.

8.7. Proiecția Din-Zbor

După cum, probabil, vă imaginați, există situații în care datele pe care doriți să le utilizați într-un GIS, sunt proiectate în diverse sisteme de coordonate de referință. De exemplu, ați putea avea un strat vectorial care prezintă granițele Africii de Sud proiectate în UTM 35S, și un alt strat vectorial, de tip punct, cu informații despre cantitatea de precipitații, proiectat în sistemul de coordonate geografice WGS 84. În GIS aceste două straturi vectoriale sunt plasate în zone total diferite ale canevasului, deoarece au proiecții diferite.

To solve this problem, many GIS include a functionality called on-the-fly projection. It means, that you can define a certain projection when you start the GIS and all layers that you then load, no matter what coordinate reference system they have, will be automatically displayed in the projection you defined. This functionality allows you to overlay layers within the map window of your GIS, even though they may be in different reference systems. In QGIS, this functionality is applied by default.

8.8. Probleme comune / lucruri de care trebuie să fiți conștienți

Subiectul proiecției de hărți este foarte complex, și nu rareori înșiși profesioniștii care au studiat geografia, geodezia sau o altă știință legată de GIS, au probleme cu definirea corectă a proiecțiilor pentru hărți și a sistemelor de coordonate de referință. De obicei, atunci când lucrați în GIS, datele de care dispuneți au deja o proiecție. În cele mai multe cazuri, aceste date sunt proiectate chiar în CRS-ul de care aveți nevoie, astfel încât nu va trebui să creați un nou sistem de referință sau să reproiectați datele dintr-un sistem în altul. Cu toate acestea, este întotdeauna util să aveți o idee despre ceea ce reprezintă proiecția hărții și CRS-ul.

8.9. Ce am învățat?

Să recapitulăm subiectele abordate în acest capitol:

• Proiecțiile hărții reprezintă suprafața pământului bi-dimensional, pe o foaie de hârtie sau pe ecranul computerului.

• Există proiecții pentru harta întregului glob, dar cele mai multe proiecții sunt create și optimizate pentru proiecția unor zone mai mici de pe suprafața pământului.

• Proiecțiile de hartă nu sunt reprezentări absolut precise ale pământului sferic. Ele prezintă denaturări de conformitate unghiulară, de distanță și de suprafață. Este imposibilă păstrarea tuturor acestor caracteristici, în același timp, într-o proiecție de hartă.

• Un Sistem de Coordonate de Referință (CRS) definește, cu ajutorul coordonatelor, modul în care harta proiectată bi-dimensional, este legată de locațiile reale de pe Terra.

• Există două tipuri diferite de sisteme de coordonate de referință: Sisteme de Coordonate Geografice și Sisteme de Coordonate Proiectate.

• Proiecția „Din zbor” este o funcționalitate în GIS, care permite suprapunerea straturilor, chiar dacă acestea sunt proiectate în sisteme de coordonate de referință diferite.

8.10. Încercați acum!

Aici sunt câteva idei care pot fi testate împreună cu elevii dumneavoastră:

1. Start QGIS

2. In Project ► Properties… ► CRS check No projection (or unknown/non-Earth projection)

3. Load two layers of the same area but with different projections

4. Let your pupils find the coordinates of several places on the two layers. You can show them that it is not possible to overlay the two layers.

5. Then define the coordinate reference system as Geographic/WGS 84 inside the Project Properties dialog

6. Load the two layers of the same area again and let your pupils see how setting a CRS for the project (hence, enabling „on-the-fly” projection) works.

7. You can open the Project Properties dialog in QGIS and show your pupils the many different Coordinate Reference Systems so they get an idea of the complexity of this topic. You can select different CRSs to display the same layer in different projections.

8.11. De reținut

Dacă nu dispuneți de un calculator puteți prezenta studenților principiile celor trei familii de proiecții pentru hărți. Luați un glob și hârtie, apoi demonstrați modul în care lucrează proiecțiile cilindrice, conice și plane, în general. Cu ajutorul unei foi transparente se poate desena un sistem de referință care arată axele X și Y ale unui sistem de coordonate bi-dimensional. Apoi, lăsați studenții să definească coordonatele (valorile X și Y) pentru diverse locuri.

8.12. Lecturi suplimentare

Cărți:

• Chang, Kang-Tsung (2006). Introducere în sistemele de informații geografice. A 3-a ediție. McGraw Hill. ISBN: 0070658986

• DeMers, Michael N. (2005). Bazele Sistemelor de Informații Geografice. A 3-a ediție. Wiley. ISBN: 9814126195

• Galati, Stephen R. (2006): Sistemele de Informații Geografice Demistificate. Artech House Inc. ISBN: 158053533X

Site-uri web:

• https://foote.geography.uconn.edu/gcraft/notes/mapproj/mapproj_f.html

• http://geology.isu.edu/wapi/geostac/Field_Exercise/topomaps/index.htm

Ghidul utilizatorului QGIS conține, de asemenea, mai multe informații detaliatedespre proiecțiile hărților din QGIS.

8.13. Ce urmează?

În secțiunea care urmează, vom arunca o privire mai atentă la Producerea Hărții.