7. Topologia
Obiective: |
Să înțelegem topologia datelor vectoriale |
|
Cuvinte cheie: |
Vector, topologie, normele de topologie, erorile de topologie, raza de căutare, distanța de acroșare, entitate simplă |
7.1. Vedere generală
Topologia exprimă relațiile spațiale dintre entitățile vectoriale conectate sau adiacente (puncte, polilinii și poligoane) dintr-un GIS. Datele topologice, sau pe bază de topologie, sunt utile pentru detectarea și corectarea erorilor de digitizare (de exemplu, două linii dintr-un strat de drumuri vectoriale care nu se întâlnesc perfect la o intersecție). Topologia este necesară pentru realizarea unor genuri de analize spațiale, cum ar fi analiza de rețea.
Imagine you travel to London. On a sightseeing tour you plan to visit St. Paul’s Cathedral first and in the afternoon Covent Garden Market for some souvenirs. Looking at the Underground map of London (see Fig. 7.10) you have to find connecting trains to get from Covent Garden to St. Paul’s. This requires topological information (data) about where it is possible to change trains. Looking at a map of the underground, the topological relationships are illustrated by circles that show connectivity.
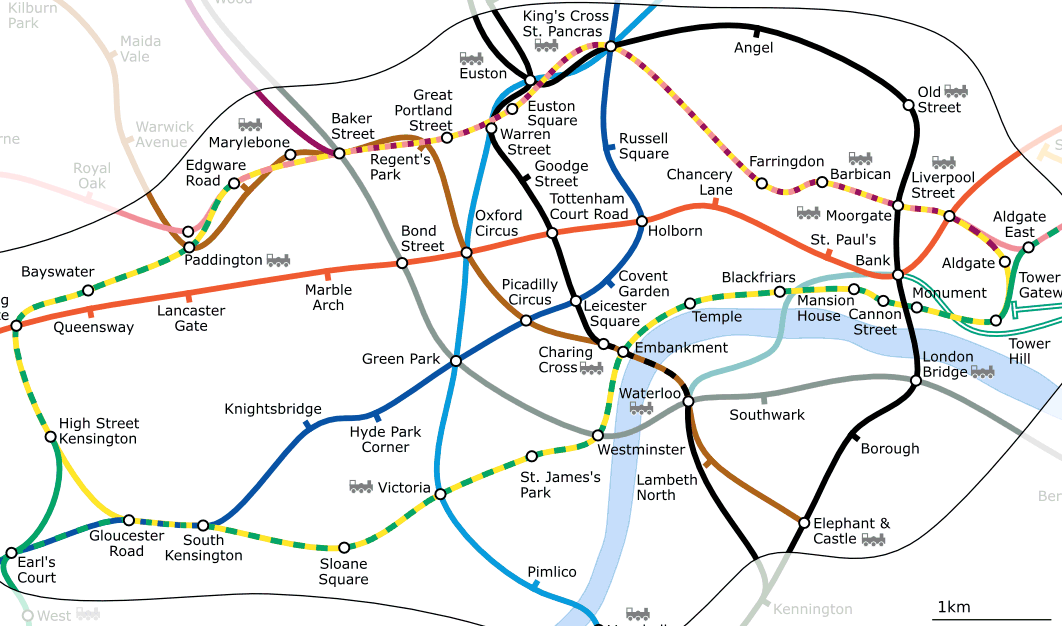
Fig. 7.10 Topologia rețelei de metrou din Londra
7.2. Erori de topologie
There are different types of topological errors and they can be grouped according to whether the vector feature types are polygons or polylines. Topological errors with polygon features can include unclosed polygons, gaps between polygon borders or overlapping polygon borders. A common topological error with polyline features is that they do not meet perfectly at a point (node). This type of error is called an undershoot if a gap exists between the lines, and an overshoot if a line ends beyond the line it should connect to (see Fig. 7.11).
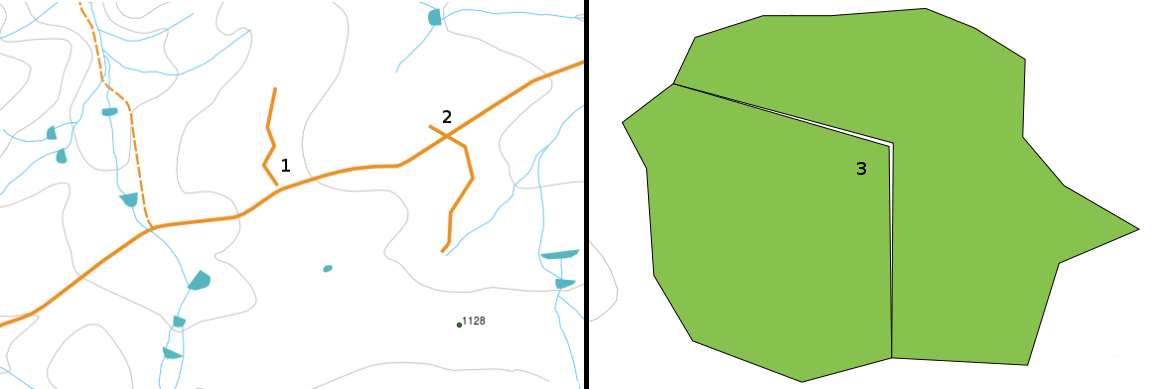
Fig. 7.11 Erorile de neîncadrare (1) apar atunci când liniile vectoriale digitizate, care ar trebuie să fie conectate între ele, nu se ating. Depășirile (2) apar atunci când o linie se termină dincolo de linia la care ar trebui să se conecteze. Așchiile (3) apar atunci când vârfurile a două poligoane nu aderă perfect la laturile lor.
Rezultatul erorilor de neîncadrare și de depășire sunt așa-numitele «noduri incerte» de la capătul liniilor. Nodurile incerte sunt acceptabile în cazuri speciale, cum ar fi cazul în care sunt atașate unor străzi care se înfundă.
Erorile topologice denaturează relațiile dintre entități. Aceste erori trebuie să fie reparate, pentru a fi în măsură să studiați datele vectoriale cu proceduri cum ar fi analiza de rețea (de exemplu, găsirea cel mai bun traseu într-o rețea de drumuri) sau prin măsurători (de exemplu, aflarea lungimii unui râu). În plus, există și alte motive pentru care este important și util să creați sau să aveți date vectoriale cu topologie corectă. Doar imaginați-vă că digitizați o hartă a granițelor municipale pentru provincia dvs., și că poligoanele se suprapun sau prezintă așchii. Dacă există astfel de erori, deși veți putea utiliza instrumentele de măsurare, rezultatele pe care le obține vor fi incorecte. Nu veți cunoaște suprafața corectă și nici nu veți fi în măsură să precizați cu exactitate unde sunt granițele dintre municipalități.
Nu este important doar pentru propria analiză să creați și să aveți date corecte din punct de vedere topologic, ci și pentru cei cărora le transmiteți datele. Aceștia se așteaptă ca datele și rezultatele analizei să fie corecte!
7.3. Reguli topologice
Din fericire, multe din erorile care pot apărea la digitizarea entităților vectoriale pot fi prevenite prin regulile de topologie care sunt implementate în multe aplicații GIS.
Cu excepția unor formate de date GIS speciale, topologia nu este, de obicei activată în mod implicit. Multe aplicații GIS comune, cum ar fi QGIS, definesc topologia sub formă de reguli relaționate, permițând utilizatorului să aleagă regulile care vor fi implementate într-un strat vectorial.
Lista de mai jos prezintă câteva exemple în care regulile topologie pot fi definite pentru entități ale lumii reale într-o hartă vectorială:
Marginile hărții unei municipalități nu trebuie să se suprapună.
Marginile unei hărți pentru o municipalitate nu trebuie să aibă lacune (șuvițe).
Poligoanele care indică limitele de proprietate trebuie să fie închise. Depășirile liniilor de frontieră, inclusiv cele negative, nu sunt permise.
Curbele de nivel dintr-un strat vectorial de tip linie nu trebuie să se intersecteze (nu au voie să se încrucișeze).
7.4. Instrumente topologice
Many GIS applications provide tools for topological editing. For example in QGIS you can enable topological editing to improve editing and maintaining common boundaries in polygon layers. A GIS such as QGIS «detects» a shared boundary in a polygon map so you only have to move the edge vertex of one polygon boundary and QGIS will ensure the updating of the other polygon boundaries as shown in Fig. 7.12 (1).
Another topological option allows you to prevent** polygon overlaps** during digitising (see Fig. 7.12 (2)). If you already have one polygon, it is possible with this option to digitise a second adjacent polygon so that both polygons overlap and QGIS then clips the second polygon to the common boundary.
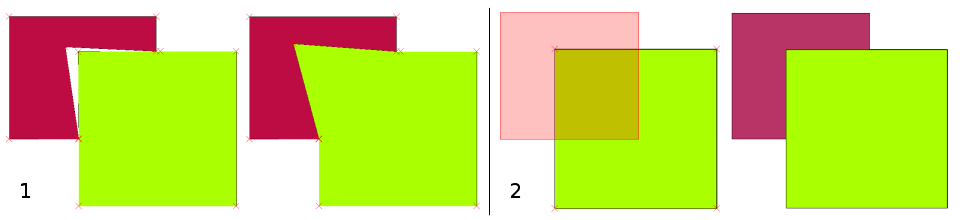
Fig. 7.12 (1) Topological editing to detect shared boundaries, when moving vertices. When moving a vertex, all features that share that vertex are updated. (2) To avoid polygon overlaps, when a new polygon is digitised (shown in red) it is clipped to avoid overlapping neighbouring areas.
7.5. Distanța de acroșare
Snapping distance is the distance a GIS uses to search for the closest vertex and / or segment you are trying to connect when you digitise. A segment is a straight line formed between two vertices in a polygon or polyline geometry. If you aren’t within the snapping distance, a GIS such as QGIS will leave the vertex where you release the mouse button, instead of snapping it to an existing vertex and / or segment (see Fig. 7.13).
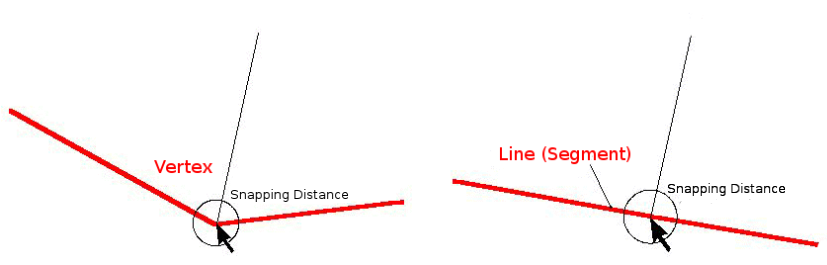
Fig. 7.13 Distanța de acroșare (cercul negru) este definită în unități de hartă (de exemplu, în grade zecimale), pentru acroșarea fie la noduri, fie la segmente.
7.6. Raza de căutare
Cautarea radiala reprezinta distanta pe care un GIS o utilizeaza in cautarea celui mai apropiat vertex cand incercati sa il mutati in momentul in care faceti click pe harta. Daca nu sunteti in cadrul cautarii radiale, GIS-ul nu va gasi si selecta nici un vertex al entitatii selectate. In principiu, este asemanatoare cu functionalitatea distanta saltului.
Distanta saltului si cautarea radiala sunt amandoua setate in unitatile de masura ale hartii deci va trebui sa faceti cateva experimente pentru a afla valoarea corecta. Daca specificati o valoare care este prea mare, GIS-ul poate sari la un alt vertex, in special cand lucrati cu un numar mare de vertexi apropriati unul de altul. Daca specificati cautarea radiala prea mica aplicatia GIS nu va gasi nici o entitate sau vertex de mutat sau de editat.
7.7. Probleme comune / lucruri de care trebuie să fiți conștienți
Mainly designed for simplicity and for fast rendering but not for data analysis that requires topology (such as finding routes across a network), many GIS applications are able to show topological and simple feature data together and some can also create, edit and analyse both.
7.8. Ce am învățat?
Să recapitulăm subiectele abordate în acest capitol:
Topologia ne arată relaţia spaţială dintre entităţile vector vecine.
Topologia în GIS poate fi accesată de către instrumentele topologice.
Topologia poate fi utilizată pentru a detecta şi corecta erorile de digitizare
Pentru anumite instrumente, precum analiza reţelei, datele topologice sunt estenţiale.
Distanţa de snap şi raza de căutare ne ajută să digitizăm corect topologic datele vector.
O entitate simplă nu reprezintă un adevărat format de date topologic, dar este frecvent utilizat de aplicațiile GIS.
7.9. Încercați acum!
Aici sunt câteva idei care pot fi testate împreună cu elevii dumneavoastră:
Marcati opririle autobuzului local pe o harta topografica si apoi dati ca sarcina elevilor dumneavoastra sa gaseasca cea mai scurta cale dintre cele doua opriri.
Gândiți-vă la modul în care ați crea entitățile vectoriale într-un GIS, pentru a reprezenta o rețea de drumuri topologice din orașul dvs. Ce reguli topologice sunt importante, și ce instrumente pot utiliza studenții dvs. în QGIS, pentru a vă asigura că noul strat cu drumuri este corect din punct de vedere topologic?
7.10. De reținut
Dacă nu aveți un calculator disponibil, puteți utiliza o hartă a rețelei de transport feroviar sau auto, apoi să discutați despre relațiile spațiale și despre topologie cu studenții.
7.11. Lecturi suplimentare
Cărți:
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Site-uri web:
Ghidul de utilizare QGIS conţine mai multe informaţii detaliate despre istrumentele de editare topologică.
7.12. Ce urmează?
In sectiunea care urmeaza vom arunca o privire de aproape asupra „Sistemelor de coordonate” pentru a intelege cum relationam datele despre pamantul sferic sferic si hartile plate.
