7. Topologia
Objetivos: |
Compreender a topologia de dados vectoriais |
|
Palavras chave: |
Vetor, topologia, regras de topologia, erros topológicos, raio de pesquisa, tolerância para a atração, característica simples |
7.1. Visão global
Topology expresses the spatial relationships between connecting or adjacent vector features (points, polylines and polygons) in a GIS. Topological or topology-based data are useful for detecting and correcting digitising errors (e.g. two lines in a roads vector layer that do not meet perfectly at an intersection). Topology is necessary for carrying out some types of spatial analysis, such as network analysis.
Imagine you travel to London. On a sightseeing tour you plan to visit St. Paul’s Cathedral first and in the afternoon Covent Garden Market for some souvenirs. Looking at the Underground map of London (see Fig. 7.10) you have to find connecting trains to get from Covent Garden to St. Paul’s. This requires topological information (data) about where it is possible to change trains. Looking at a map of the underground, the topological relationships are illustrated by circles that show connectivity.
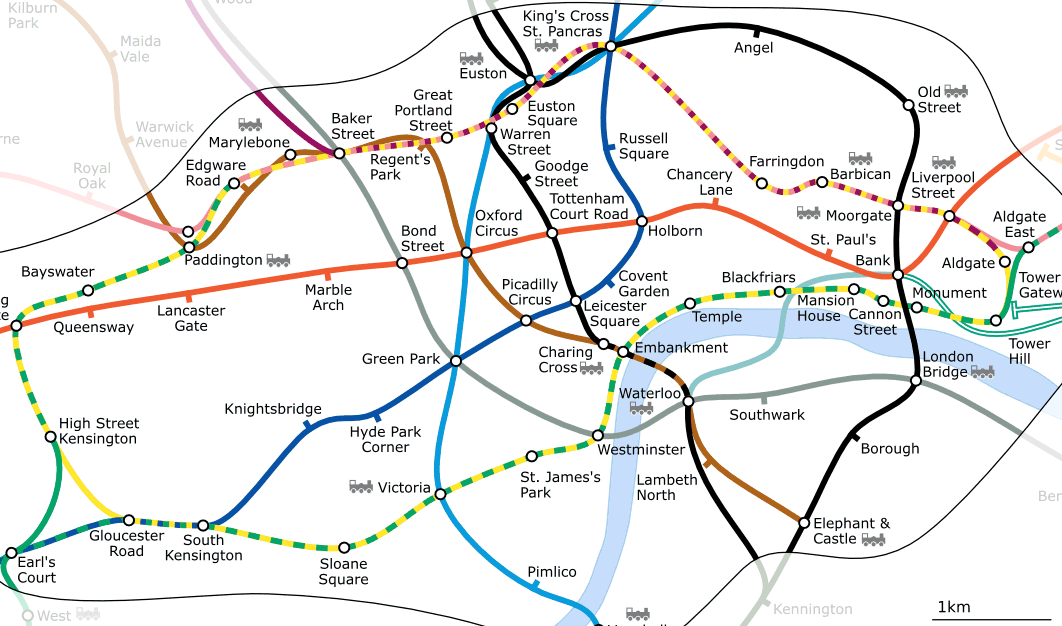
Fig. 7.10 Topologia da rede do metro de Londres.
7.2. Erros topológicos
There are different types of topological errors and they can be grouped according to whether the vector feature types are polygons or polylines. Topological errors with polygon features can include unclosed polygons, gaps between polygon borders or overlapping polygon borders. A common topological error with polyline features is that they do not meet perfectly at a point (node). This type of error is called an undershoot if a gap exists between the lines, and an overshoot if a line ends beyond the line it should connect to (see Fig. 7.11).
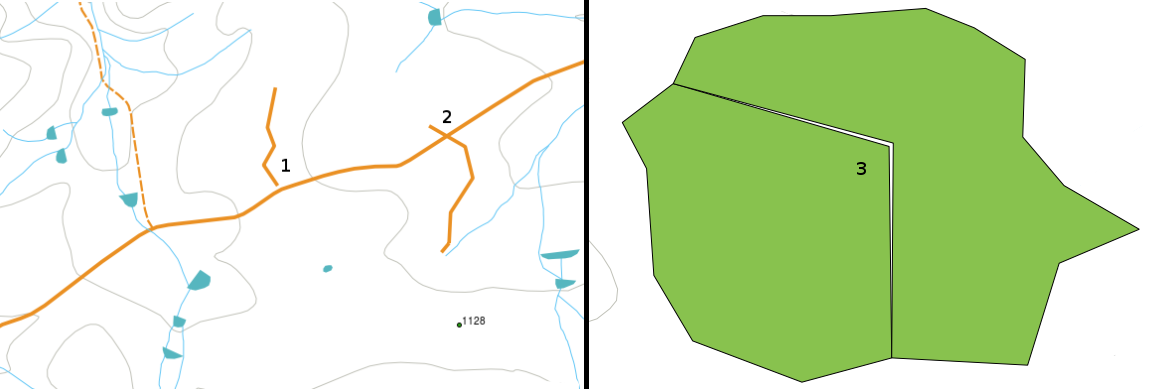
Fig. 7.11 Sem ligação (1) ocorre quando as linhas de vetores digitalizados que não se tocam e que deviam estar conectadas umas nas outras. Sobreposição (2) acontece se uma linha termina para além da linha que deve se conectar. Falhas (3) ocorrem quando os vértices de dois polígonos não se igualam nas fronteiras.
Os erros «sem ligação» e «sobreposição» resultam nos chamados “nós pendentes” na extremidade das linhas. Estes nós pendentes são admissíveis em casos especiais, por exemplo, quando correspondem ao extremo de ruas ou outras vias sem continuidade.
Os erros topológicos quebram a relação entre elementos. Esses erros precisam de ser corrigidos para assim parmitir analisar os dados vetoriais com procedimentos como a análise de redes (ex. encontrar o melhor trajeto numa rede viária) ou medida (ex. encontrar o comprimento de um rio). Para além de a topologia ser útil para a análise de redes e medidas, há outros motivos importantes e úteis para criar e ter dados vetoriais com a topologia correta. Imagine que digitaliza um mapa com os limites municipais para a sua regição e os polígonos sobrepõem-se ou têm falhas. Se houver erros destes, pode ser possível utilizar ferramentas de medição, mas os resultados estarão incorretos. Pode não conhecer a área correta de um município e não vai ser possível definir com exatigão onde se localizam os limites dos municípios.
É importante não só para a sua própria análise para criar e ter dados topologicamente corretos, mas também para as pessoas que fornece os dados. Estarão à espera dos dados e a análise dos resultados correctas.
7.3. Regras topológicas
Felizmente, os erros mais comuns podem ocorrer quando digitalizamos elementos vectoriais podem ser prevenidas por regras de topologia que estão implementadas em muitas aplicações SIG.
Excepto para alguns formatos de dados SIG especiais, a topologia geralmente não é imposta por defeito. Muitos SIG comuns, como QGIS, define a topologia como as regras de relação e permite que o utilizador escolha as regras, se houver, a ser implementada numa camada vetorial.
A lista a seguir mostra alguns exemplos onde as regras de topologia podem ser definidas para os recursos do mundo real num mapa vetorial:
As áreas de bordadura dos municipios não se podem sobrepôr
As áreas de bordadura dos municipios não podem ter buracos (slivers)
Os polígonos mostram os limites da propriedade que devem ser fechados. Ultrapassar ou não cruzar o limite não é permitido.
As linhas de contorno numa camada vectorial linha não se devem intersectar (cruzar com outra).
7.4. Ferramentas topológicas
Many GIS applications provide tools for topological editing. For example in QGIS you can enable topological editing to improve editing and maintaining common boundaries in polygon layers. A GIS such as QGIS “detects” a shared boundary in a polygon map so you only have to move the edge vertex of one polygon boundary and QGIS will ensure the updating of the other polygon boundaries as shown in Fig. 7.12 (1).
Another topological option allows you to prevent** polygon overlaps** during digitising (see Fig. 7.12 (2)). If you already have one polygon, it is possible with this option to digitise a second adjacent polygon so that both polygons overlap and QGIS then clips the second polygon to the common boundary.
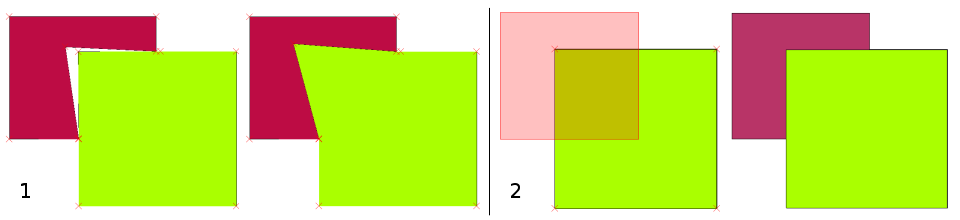
Fig. 7.12 (1) Topological editing to detect shared boundaries, when moving vertices. When moving a vertex, all features that share that vertex are updated. (2) To avoid polygon overlaps, when a new polygon is digitised (shown in red) it is clipped to avoid overlapping neighbouring areas.
7.5. Tolerância de Atracção
Snapping distance is the distance a GIS uses to search for the closest vertex and / or segment you are trying to connect when you digitise. A segment is a straight line formed between two vertices in a polygon or polyline geometry. If you aren’t within the snapping distance, a GIS such as QGIS will leave the vertex where you release the mouse button, instead of snapping it to an existing vertex and / or segment (see Fig. 7.13).
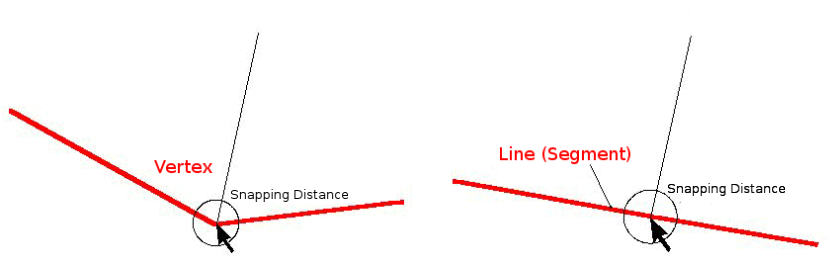
Fig. 7.13 A distância de tolerância (círculo preto) é definida nas unidades do mapa (ex. em graus decimais) para a atração de vértices ou segmentos.
7.6. Raio de pesquisa
O raio de pesquisa é a distância que um SIG utiliza para detetar o vértice mais próximo que está a tentar mover quando clica no mapa. Se não está está no raio de pesquisa, o SIG não vai encontrar e selecionar qualquer vértice de um elemento para edição. Por princípio, é relativamente semelhante á função de distância de tolerância.
Tanto a distância de tolerância como o raio de pesquisa são definidos nas unidades do mapa, pelo que pode ter que experimentar para definir o valor correto. Se especificar um valor que é demasiado grande, o SIG pode detetar o vértice errado, especialmente quando se está a trabalhar com um grande número de vértices próximos entre si. Se especificar um valor demasiado baixo, a aplicação SIG não vai encontrar elementos ou vértices para mover ou editar.
7.7. Problemas comuns / aspectos a ter em conta
Mainly designed for simplicity and for fast rendering but not for data analysis that requires topology (such as finding routes across a network), many GIS applications are able to show topological and simple feature data together and some can also create, edit and analyse both.
7.8. O que é que aprendemos?
Vamos encerrar o que aprendemos nesta folha de trabalho:
Topologia mostra a relação espacial de caracteristicas vectoriais vizinhas.
Topologia em SIG é fornecida pelas Ferramentas topológicas.
A topologia pode ser usada para detectar e corrigir erros de digitalização
Para algumas ferramentas, tais como analise de redes a topologia é essencial.
A distância de tolerância e a distância de pesquisa ajudam-nos a digilitalizar dados vetoriais corretamente.
Os dados de elementos simples não são um formato de dados topológicos verdadeiro, mas são frequentemente utilizados em aplicações SIG.
7.9. Agora tente!
Aqui estão algumas ideias para tentar com os seus alunos:
Marque os locais de paragem do autocarro numa camada e depois dê como tarefa aos seus alunos encontrar o caminho mais curto entre dois pontos de paragem.
Pense como poderia criar características de um vetor num SIG para representar uma rede topológica de estradas da sua cidade. Que regras topológicas são importantes e quais ferramentas podem usar os seus alunos no QGIS para se certificar de que a nova camada de estradas está topologicamente correta?
7.10. Algo para pensar
Se não tiver um computador disponível, pode usar um mapa das vias de circulação de autocarros ou das linhas de comboio e discutir as relações espaciais e topologia com os seus alunos.
7.11. Leitura recomendada
Livros:
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Websites:
O Guia do Utilizador do QGIS também tem informações mais detalhadas sobre a edição topológica previsto no QGIS.
7.12. Qual é a seguir?
Na secção seguinte, vamos ver mais de perto ** Sistemas de Coordenadas de Referência ** para entender como relacionamos os nossos dados esféricos da terra com os dados planos!
