17.23. Plus d’interpolation
Note
Ce chapitre montre un autre cas pratique où les algorithmes d’interpolation sont utilisés.
L’interpolation est une technique commune, et elle peut être utilisée pour démontrer plusieurs techniques qui peuvent être appliquées en utilisant le module de traitements QGIS. Cette leçon utilise certains algorithmes d’interpolation qui ont déjà été introduits, mais utilise une approche différente.
Les données pour cette leçon contiennent également une couche de points, dans ce cas avec des données d’élévation. Nous allons les interpoler principalement de la même façon que nous l’avons fait dans la leçon précédente, mais cette fois nous sauvegarderons une partie des données originales pour les utiliser pour évaluer la qualité du processus d’interpolation.
Premièrement, nous devons pixeliser la couche de points et remplir les cellules no–data résultantes, mais en utilisant seulement une fraction des points dans la couche. Nous sauvegarderons 10% des points pour une prochaine vérification, donc nous avons besoin de 90% des points prêts pour l’interpolation. Pour se faire, nous pourrions utiliser l’algorithme Séparer une couche de formes aléatoirement, que nous avons déjà utilisé dans une précédente leçon, mais il y a une meilleure manière de faire cela, sans avoir à créer une nouvelle couche intermédiaire. À la place de cela, nous pouvons simplement sélectionner les points que nous voulons utiliser pour l’interpolation (la fraction de 90%), puis exécuter l’algorithme. Comme nous l’avons déjà vu, l’algorithme de pixelisation utilisera seulement les points sélectionnés et ignorera le reste. La sélection peut être faite en utilisant l’algorithme Sélection aléatoire. Lancez-le avec les paramètres suivants.
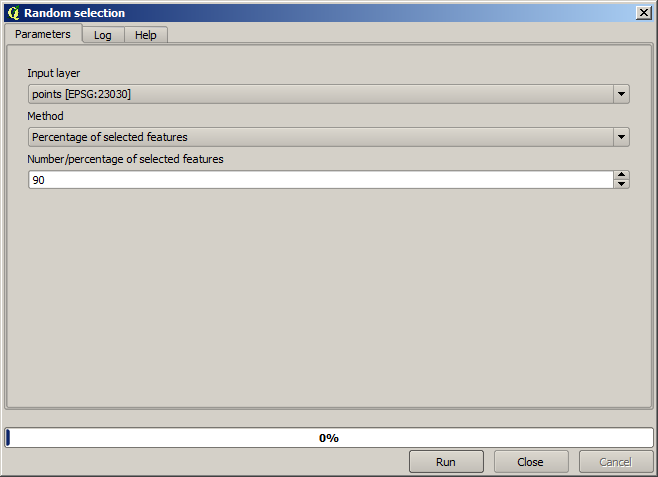
Cela va sélectionner 90% des points dans la couche à pixeliser

La sélection est aléatoire, donc votre sélection devrait différer de la sélection montrée dans l’image ci-dessus.
Exécutez maintenant l’algorithme Rastériser pour obtenir la première couche raster, et ensuite exécutez l’algorithme Combler les lacunes pour remplir les cellules sans–données [Résolution de cellule : 100 m].

Pour vérifier la qualité de l’interpolation, nous pouvons maintenant utiliser les points qui n’ont pas été sélectionnés. Nous connaissons, en ce point, l’élévation réelle (la valeur dans la couche de points) ainsi que l’élévation interpolée (la valeur présente dans la couche raster interpolée). Nous pouvons comparer les deux en calculant leur différence.
Comme nous allons d’abord utiliser les points qui ne sont pas sélectionné, inversons la sélection.

Les points contiennent la valeur originale, mais pas celles de l’interpolation. Pour les ajouter dans un nouveau champ, nous pouvons utiliser l’algorithme Ajouter des valeurs de raster aux points.
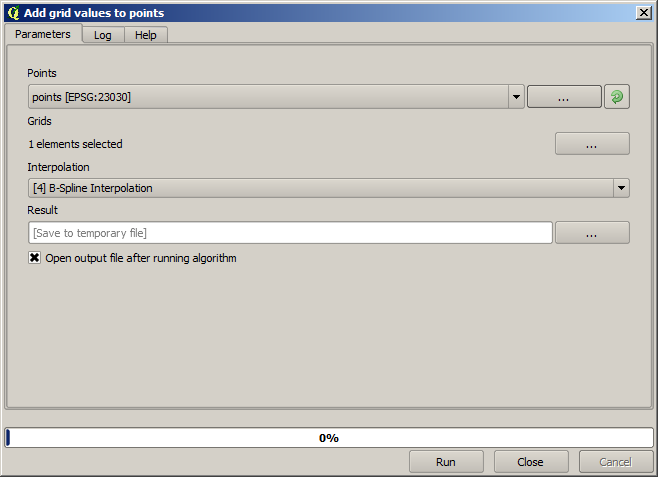
La couche raster à sélectionner (l’algorithme supporte plusieurs rasters, mais nous n’en avons besoin que d’un) est celle qui résulte de l’interpolation. Nous l’avons renommée interpolation et ce nom de couche est celui qui sera utilisé pour le nom du champ à ajouter.
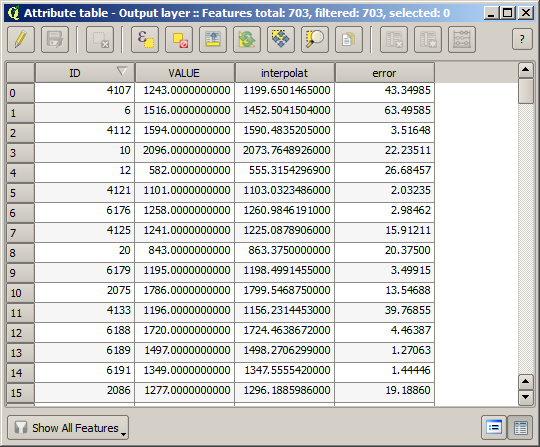
Nous avons maintenant une couche vecteur qui contient ces deux valeurs, avec des points qui n’étaient pas utilisé pour l’interpolation.
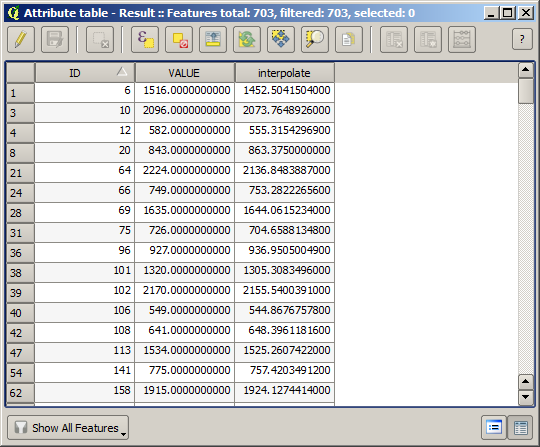
Maintenant, nous utiliserons la calculatrice de champs pour cette tâche. Ouvrez l’algorithme Calculatrice de champs et exécutez-le avec les paramètres suivants.
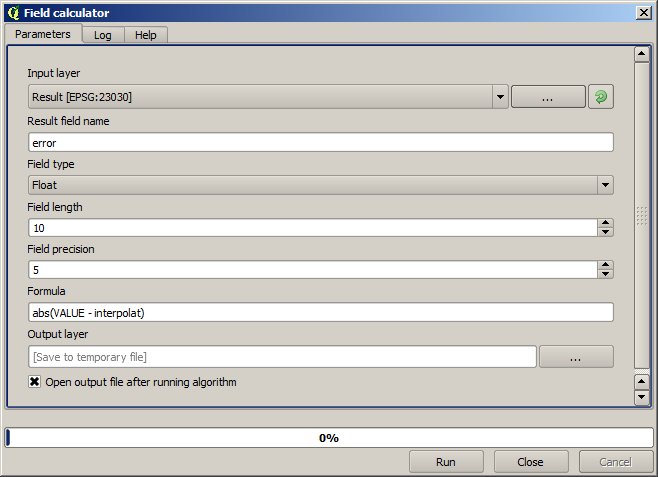
Si votre champ avec les valeurs de la couche raster a un nom différent, vous devrez modifier la formule ci-dessus en conséquence. En exécutant cet algorithme, vous obtiendrez une nouvelle couche avec uniquement les points que nous n’avons pas utilisé pour l’interpolation, chacun d’eux contenant la différence entre les deux valeurs d’élévation.
Représenter cette couche selon cette valeur nous donnera une première idée d’où se trouvent les grands écarts.
Interpoler cette couche vous donnera une couche raster avec l’erreur estimée dans tous les points de la zone interpolée.
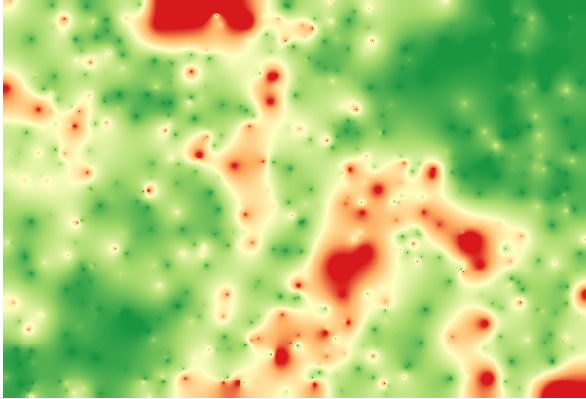
Vous pouvez aussi obtenir la même information (différence entre les valeurs des points d’origine et ceux interpolés) directement avec .
Vos résultats devrait différer de ceux-ci, car il y a une composante aléatoire introduite lors de l’exécution de la sélection aléatoire, au début de cette leçon.