11. Analyse Spatiale (Interpolation)
Objectifs : |
Compréhension de l’interpolation comme une part de l’analyse spatiale |
|
Mots clés : |
Données ponctuelles, méthode d’interpolation, Pondération par l’Inverse de la Distance, Réseau Irrégulier Triangulé |
11.1. Aperçu
L”analyse spatiale est le processus de manipulation de l’information spatiale pour extraire de nouvelles informations à partir des données originales. Habituellement, l’analyse spatiale est réalisée avec un Système d’Information Géographique (SIG). Un SIG fournit généralement des outils d’analyses spatiales pour le calcul de statistiques sur les entités et la réalisation de géotraitements comme l’interpolation des données. En hydrologie, les utilisateurs souligneront probablement l’importance de l’analyse de terrain et de la modélisation hydrologique (modélisation de la circulation de l’eau en surface et en profondeur de la terre). Dans la gestion de la faune, les utilisateurs sont intéressés par des fonctions analytiques traitant de la localisation des points de faune et leurs relations à l’environnement. Chaque utilisateur sera intéressé par différentes choses en fonction du type de travail qu’il fait.
11.2. L’Interpolation spatiale en détail
L’interpolation spatiale est le processus d’utilisation de points dont les valeurs sont connues pour estimer des valeurs à d’autres points inconnus. Par exemple, pour faire une carte des précipitations (pluie) de votre pays, vous ne trouverez pas assez de stations météo réparties uniformément pour couvrir l’intégralité de la région. L’interpolation spatiale peut estimer la température à des endroits sans données enregistrées en utilisant des relevés de températures connus dans des stations météo à proximité (voir Fig. 11.40). Ce type de surface d’interpolation est souvent appelé surface statistique. Les données d’altitude, de précipitations, d’accumulation de neige, de table d’eau et de densité de population sont d’autres types de données qui peuvent être calculées par interpolation.
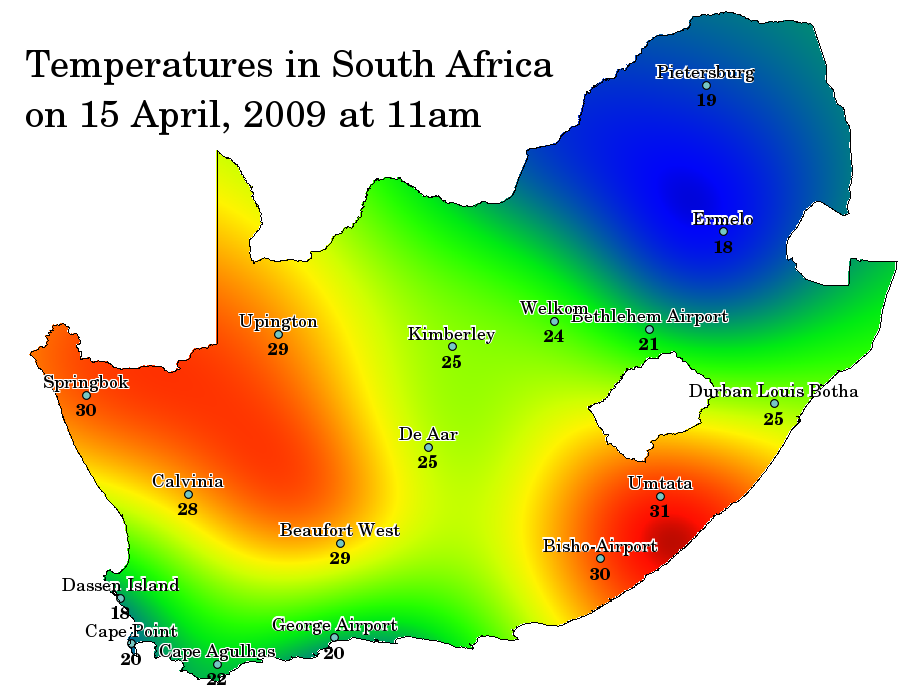
Fig. 11.40 Carte de température interpolée avec les stations météo d’Afrique du Sud.
En raison du coût élevé et de ressources limitées, la collecte de données n’est généralement menée que dans sur nombre limité d’emplacements de points sélectionnés. Dans les SIG, l’interpolation spatiale de ces points peut être appliquée pour créer une surface raster avec les estimations faites pour toutes les cellules raster.
Afin de générer une carte continue, par exemple une carte d’élévation numérique à partir de points d’altitude mesurés avec un appareil GPS, une méthode d’interpolation adaptée doit être utilisée pour estimer de manière optimale les valeurs à ces endroits où aucun des échantillons ou mesures n’ont été pris. Les résultats de l’analyse d’interpolation peuvent ensuite être utilisés pour les analyses qui couvrent la zone entière et pour la modélisation.
Il existe plusieurs méthodes d’interpolation. Dans cette introduction, nous présenterons deux méthodes largement utilisées, à savoir la Pondération par l’Inverse de la Distance (IDW) et l”Interpolation Triangulaire (TIN). Si vous recherchez des méthodes d’interpolation supplémentaires, veuillez vous reporter à la section “Pour aller plus loin” à la fin de cette rubrique.
11.3. Pondération par l’Inverse de la Distance (IDW)
Dans la méthode d’interpolation IDW, les points d’échantillons sont pondérés durant l’interpolation de telle sorte que l’influence d’un point par rapport à un autre décline avec la distance du point inconnu que vous voulez créer (voir Fig. 11.41).
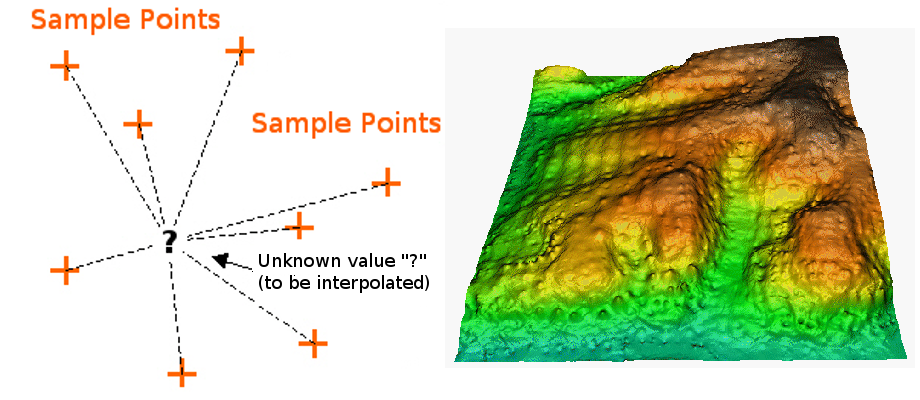
Fig. 11.41 Interpolation par pondération par l’inverse de la distance (IDW) basée sur la distance pondérée d’un jeu de points (gauche). Surface interpolée par IDW à partir de points d’élévation vecteur (droite). Source de l’image : Mitas, L., Mitasova, H. (1999).
La pondération est appliquée à un échantillon de points par le biais de l’utilisation d’un coefficient de pondération qui contrôle comment l’influence de la pondération diminuera quand la distance augmente. Plus le coefficient de pondération est grand, moins les points auront d’effet s’ils sont loin du point inconnu durant le processus d’interpolation. Quand le coefficient augmente, la valeur du point inconnu s’approche de la valeur du point d’observation le plus proche.
Il est important de noter que la méthode d’interpolation IDW a aussi des désavantages : la qualité du résultat d’interpolation peut diminuer si la distribution des points d’échantillonnage est irrégulière. De plus, les valeurs maximales et minimales dans la surface interpolée peuvent seulement se produire aux points d’échantillonnage. Il en résulte souvent des petits pics et creux autour des points de données échantillon, comme montré dans Fig. 11.41.
En SIG, les résultats d’interpolation sont souvent montrés dans une couche raster en 2 dimensions. Dans Fig. 11.42, vous pouvez voir un résultat typique d’interpolation IDW basée sur des points d’échantillonnage d’élévation collectés sur le terrain avec un dispositif GPS.
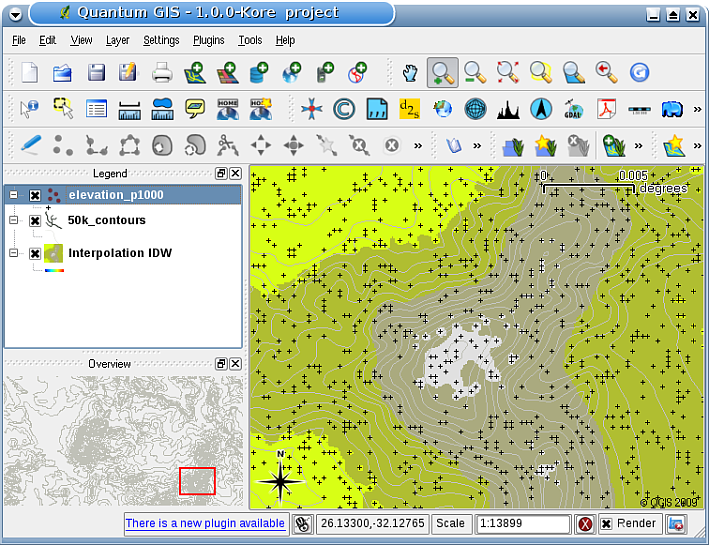
Fig. 11.42 Le résultat d’interpolation IDW à partir des points irréguliers d’échantillon d’élévation collectés (montrés avec des croix noires).
11.4. Interpolation triangulaire (TIN)
L’interpolation TIN est un autre outil populaire en SIG. Un algorithme TIN commun est appelé Triangulation de Delaunay. Il tente de créer une surface de triangles formés par des points voisins les plus proches. Pour faire ceci, les cercles circonscrits autour des points d’échantillon sélectionnés sont créés et leurs intersections sont connectées à un réseau de triangles non superposés et aussi compacts que possible (voir Fig. 11.43).
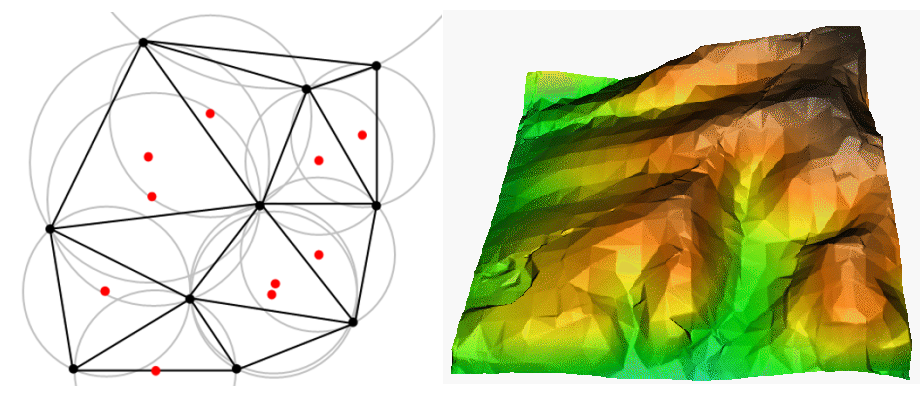
Fig. 11.43 Triangulation de Delaunay avec des cercles circonscrits autour des données d’échantillon rouges. La surface résultante de l’interpolation TIN créée à partir des points vecteurs d’élévation est montrée sur la droite. Source de l’image : Mitas, L., Mitasova, H. (1999).
Le principal inconvénient de l’interpolation TIN est que les surfaces ne sont pas lisses et peuvent donner un aspect irrégulier. Cela est dû à des pentes discontinues sur les bords du triangle et des points de données d’échantillons. En outre, la triangulation ne convient généralement pas pour l’extrapolation au-delà de la zone avec des points de données d’échantillons collectés (voir Fig. 11.44).
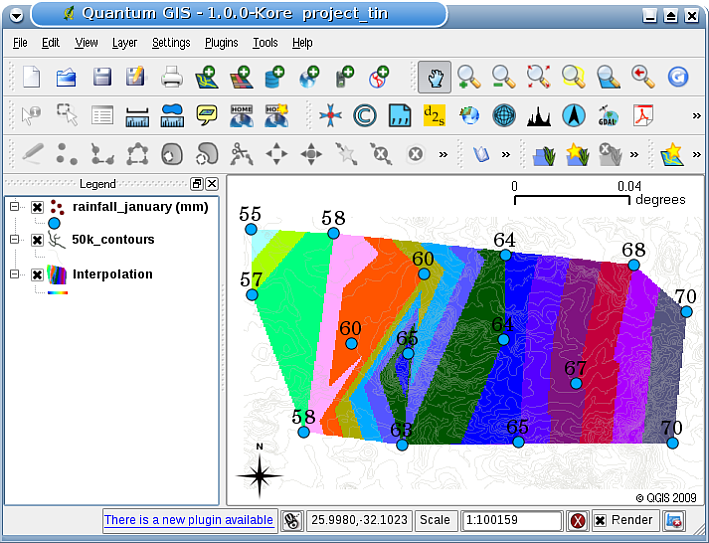
Fig. 11.44 Résultat de l’interpolation TIN de Delaunay à partir de points d’échantillon de précipitations récoltés irrégulièrement (cercles bleus).
11.5. Problèmes courants / Choses à savoir
Il est important de se souvenir qu’il n’y a pas de méthode unique d’interpolation qui peut être appliquée à toutes les situations. Certaines sont plus exactes et utiles que d’autres mais prennent du temps à calculer. Elles ont toutes des avantages et des désavantages. En pratique, le choix d’une méthode particulière d’interpolation devrait dépendre des données d’échantillon, du type de surfaces qui doivent être générées et de la tolérance de l’estimation des erreurs. Généralement, une procédure en trois étapes est recommandée :
Évaluer les données d’échantillon. Faites ceci pour avoir une idée de comment les données sont distribuées dans la zone car cela peut fournir des conseils sur la méthode d’interpolation à utiliser.
Appliquer une méthode d’interpolation qui est la plus appropriée à la fois pour les données d’échantillon et les objectifs de l’étude. Lorsque vous doutez, essayez plusieurs méthodes, si disponible.
Comparer les résultats et trouver le meilleur résultat et la méthode la plus appropriée. Ceci peut ressembler à un processus qui prend au début du temps. Cependant, dès que vous gagnez en expérience et en connaissance des différentes méthodes d’interpolation, le temps requis pour la génération de la surface la plus appropriée sera grandement réduit.
11.6. Autres méthodes d’interpolation
Bien que nous nous sommes concentrés sur les méthodes d’interpolation IDW et TIN dans cette partie, il y a plus de méthodes d’interpolation spatiale fournies dans les SIG, comme une interpolation de Spline Régularisé avec Tension (RST), le krigeage ou une interpolation de Surface de Tendance. Voir la section de lecture supplémentaire ci-dessous pour un lien web.
11.7. Qu’avons-nous appris?
Faisons le point sur ce que nous avons abordé dans cette partie:
L”Interpolation utilise des points vecteur avec des valeurs connues pour estimer des valeurs à des positions inconnues pour créer une surface raster couvrant une zone entière.
Le résultat d’interpolation est typiquement une couche raster.
Il est important de trouver une méthode d’interpolation pertinente pour estimer les valeurs des positions inconnues de façon optimale.
L”Interpolation IDW donne les poids des points d’échantillon de telle sorte que l’influence d’un point sur un autre diminue avec la distance à partir du nouveau point estimé.
L”Interpolation TIN utilise des points d’échantillon pour créer une surface formée par des triangles basés sur l’information du point voisin le plus proche.
11.8. Maintenant, essayez !
Voici quelques pistes d’actions à essayer avec vos élèves:
Le ministère de l’Agriculture souhaite cultiver de nouvelles terres dans votre région mais, mis à part les caractéristiques des sols, il souhaite savoir si la pluviométrie sera suffisante pour assurer un bon rendement. Toutes les informations dont il dispose proviennent des stations météo de la région. Créez avec vos étudiants une surface interpolée qui délimite les zones recevant le plus de précipitations.
L’office du tourisme veut publier des informations sur les conditions météo en janvier et février. Il possède des données de températures, de précipitations et de force de vent et vous demande d’interpoler leurs données pour estimer les endroits où les touristes auront probablement les conditions météos optimales avec des températures douces, pas de précipitations et une petite force de vent. Pouvez-vous identifier les endroits dans votre région qui rencontrent ces critères ?
11.9. Il faut y réfléchir.
Si vous n’avez pas d’ordinateur disponible, vous pouvez utiliser une feuille topo et une règle pour estimer les valeurs d’élévation entre les lignes de contour ou les valeurs de précipitations entre les stations météo fictives. Par exemple, si les précipitations à la station météo A sont de 50mm par mois et à la station B de 90mm, on peut estimer que les précipitations à la moitié de la distance entre la station A et la station B sont de 70mm.
11.10. Pour aller plus loin
Livres :
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005): Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Mitas, L., Mitasova, H. (1999). Spatial Interpolation. In: P.Longley, M.F. Goodchild, D.J. Maguire, D.W.Rhind (Eds.), Geographical Information Systems: Principles, Techniques, Management and Applications, Wiley.
Sites Web :
Le Guide de l’Utilisateur de QGIS contient également plus d’informations détaillées sur les outils d’interpolation avec QGIS.
11.11. La suite ?
C’est la dernière partie de cette série. Nous vous encourageons à explorer QGIS et à utiliser le manuel d’accompagnement QGIS pour découvrir toutes les autres choses que vous pouvez faire avec le logiciel de SIG !
