8. 좌표계

	목적	좌표계 이해하기
	키워드	좌표계(Coordinate Reference System), 맵 투영(Map Projection), 실시간 투영(On the Fly Projection), 위도, 경도, 편북(偏北, Northing), 편동(偏東, Easting)

8.1. 개요

맵 투영(map projection) 이란 지구의 표면, 또는 지표면의 일부를 평평한 종이 또는 컴퓨터 스크린 위에 재현하려는 행위입니다. 간단히 말하자면, 맵 투영은 지구의 구(球) 형태(3D)를 평면 형태(2D)로 변형시키려는 행위입니다.

좌표계(coordinate reference system, CRS) 는 그 후 GIS에 저장된 2차원의 투영된 맵이 어떻게 지구 상의 실재 위치에 연결되는지를 정의합니다. 어떤 맵 투영법과 좌표계를 사용할지는 여러분이 작업하고자 하는 영역의 지역적 범위, 여러분이 분석하고자 하는 대상, 마지막으로 어떤 데이터를 사용할 수 있는지에 따라 결정됩니다.

8.2. 맵 투영을 더 자세히

지구의 형태를 표현하는 전통적인 방법 가운데 하나가 바로 지구본입니다. 하지만 이 방법에는 문제가 하나 있습니다. 지구본이 지구의 형태를 완벽에 가깝게 보전하고 대륙 크기의 객체들의 공간 구조(spatial configuration)를 표현하지만, 한 사람이 들고 다니기엔 힘들죠. 또 사용하기 편하려면 극도로 소축척(예: 1:1억)이어야 합니다.

GIS 응용 프로그램에서 흔히 사용하는 주제도 데이터 대부분은 훨씬 대축척입니다. 전형적인 GIS 데이터셋의 축척은 세부사항의 수준에 따라 다르지만 최소 1:250,000 이상입니다. 지구본을 이 축척으로 만든다면 생산 비용은 물론 난이도도 높겠지만 들고 다니기는 더 어려울 겁니다. 그 결과 지도 제작자들은 구 형태의 지구를 2차원으로 – 합리적인 정확도와 함께 – 보여줄 수 있는 맵 투영 이라는 일련의 기술들을 개발하게 된 것입니다.

근거리에서 관찰할 경우 지구는 상대적으로 평평해 보입니다. 하지만 우주에서 관찰하는 경우, 지구가 상대적으로 구 형태라는 사실을 알 수 있죠. 다음에 나올 맵 생성 단원에서 배울 것이지만, 지도란 실재(reality)를 표현합니다. 지도는 객체뿐만이 아니라 객체의 형태와 공간 배열(spatial arrangement)도 표현할 수 있도록 설계되었습니다. 각 맵 투영법은 장점 과 단점 을 함께 가지고 있습니다. 어떤 맵을 위한 최적의 투영법은 맵의 축척 및 맵의 용도에 따라 달라집니다. 예를 들면 어떤 투영법은 아프리카 대륙 전체를 지도로 만드는 데 사용하는 경우 용납할 수 없는 왜곡을 발생시킬 수도 있지만, 어떤 나라의 대축척(상세) 지도 를 만드는 경우엔 훌륭한 선택이 될 수도 있습니다. 맵 투영법의 속성들이 지도의 몇몇 객체들을 설계하는 데 영향을 줄 수도 있습니다. 일부 투영법들은 좁은 지역에 사용하기 적합하지만, 다른 일부는 동서 범위로 긴 지역을 지도로 만드는 데 적합하고 또다른 일부는 남북 범위로 긴 지역을 지도로 만드는 데 더 적합합니다.

8.3. 맵 투영법 삼족(三族)

맵 투영을 생성하는 과정은 표면에 불투명한 객체들이 있는 투명한 지구본 안에서 광원을 비춘다는 것으로 가장 잘 설명할 수 있습니다. 그렇게 각 객체의 외곽선을 2차원의 평평한 종이 한 장에 투영하는 거죠. 서로 다른 투영 방법들은 이 지구본을 원통형 종이로 감싸느냐, 원뿔형 종이로 감싸느냐, 아니면 평면 에 투영하느냐에 따른 차이입니다. 이 방법들을 각각 맵 투영법의 일족(一族) 이라 합니다. 즉, 평면 투영법 의 일족, 원통 투영법 의 일족, 원뿔 투영법 의 일족이 존재합니다. (그림 8.3 을 참조하세요.)

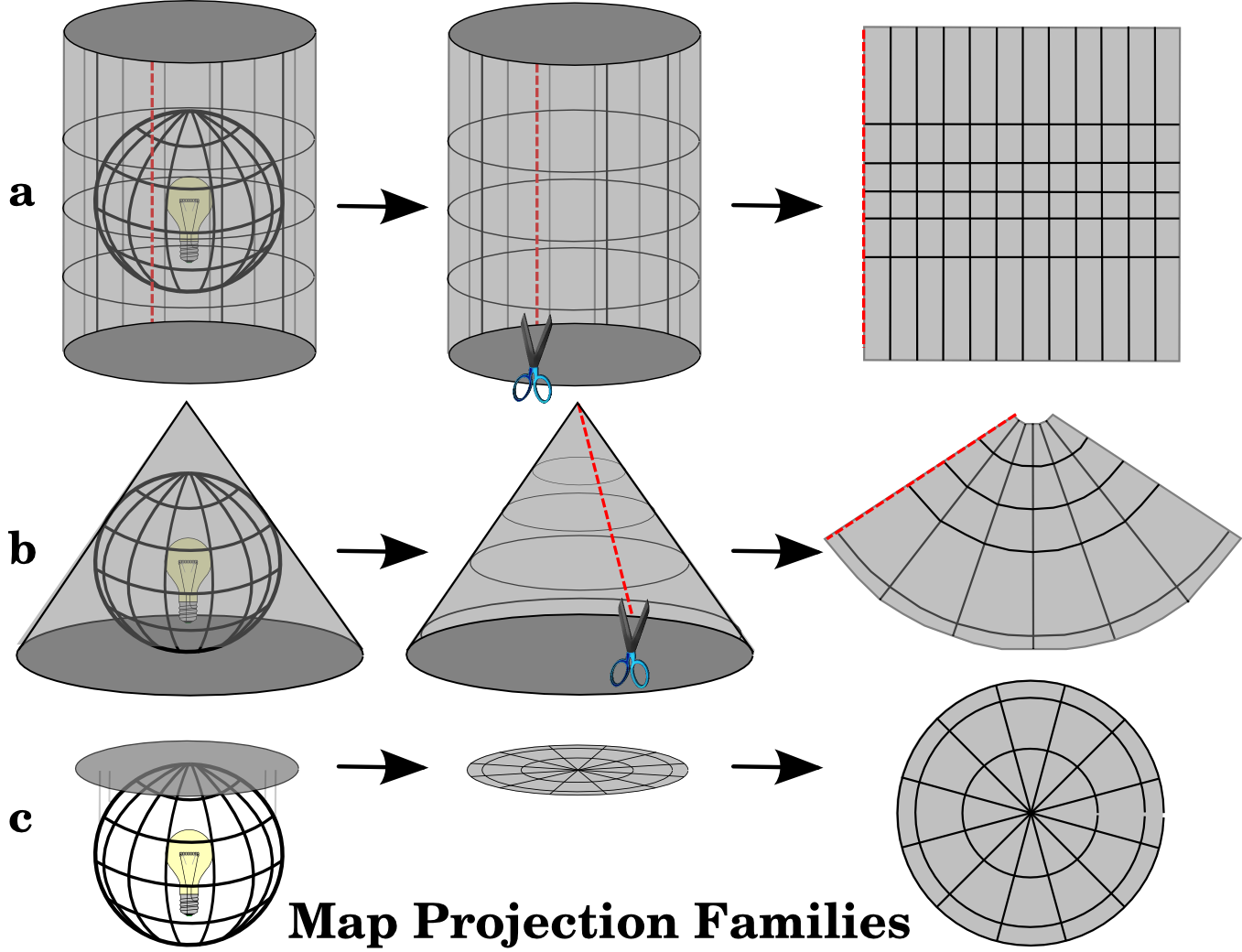
그림 8.3 맵 투영법 삼족입니다. 각각 ⓐ원통 투영법, ⓑ원뿔 투영법, ⓒ평면 투영법으로 대표됩니다.

물론 오늘날 구형 지구를 평평한 종이 위에 투영하는 과정은 기하학과 삼각법이라는 수학 원리를 이용해 이루어집니다. 이렇게 지구본 안에서 빛을 비춘다는 물리적인 투영을 재현하는 거죠.

8.4. 맵 투영의 정확도

맵 투영은 절대 구형 지구를 완전히 정확하게 표현할 수 없습니다. 맵 투영 과정의 결과, 모든 지도는 각도 정합(angular conformity), 거리 그리고 면적의 왜곡 을 보이게 됩니다. 어떤 맵 투영법이든 이런 특성들을 몇 가지 가지고 있을 수 있으며, 때로는 어느 정도 합리적인 선 안에서 면적, 거리 및 각도 정합이라는 모든 속성들의 왜곡을 받아들이기도 합니다. 이렇게 타협한 투영법의 예로는 세계 지도를 생성하고 가시화하는 데 자주 쓰이는 빈켈 트리펠(Winkel tripel) 투영법 과 로빈슨(Robinson) 투영법 을 들 수 있습니다. (로빈슨 투영법의 경우 그림 8.4 를 참조하세요.)

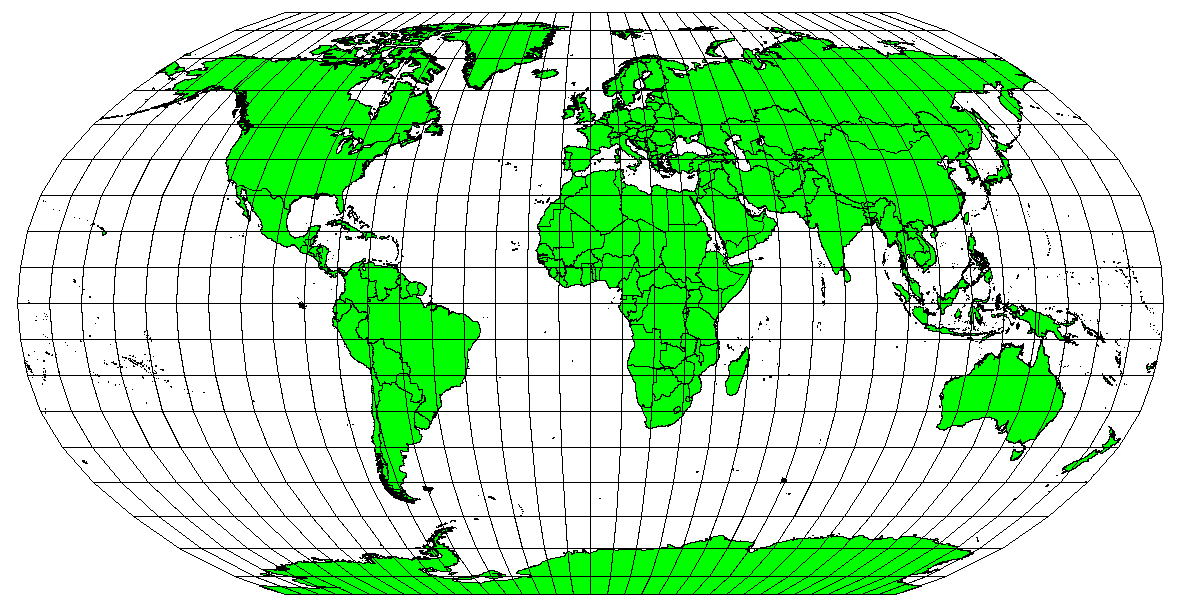
그림 8.4 로빈슨 투영법은 면적, 각도 정합 및 거리의 왜곡을 받아들여 타협한 투영법입니다.

맵 투영 시 이 모든 특성을 동시에 보전하는 것은 일반적으로 불가능합니다. 즉 여러분이 정확한 분석 작업을 수행하려는 경우 해당 분석에 가장 적합한 특성을 제공하는 맵 투영법을 사용해야 한다는 뜻입니다. 예를 들어 맵 상에서 거리를 측정해야 한다면 가장 정확한 거리를 제공하는 투영법을 데이터에 적용해야 할 것입니다.

8.4.1. 각도 정합이 뛰어난 맵 투영법

지구본으로 작업하는 경우, 나침반의 주 방위(동서남북)는 언제나 서로 90도를 유지할 것입니다. 달리 말하자면 동쪽은 언제나 북쪽에서 시계 방향으로 90도 방향입니다. 맵 투영 시에도 정확한 각도 속성 을 유지할 수 있습니다. 이렇게 각도 정합이라는 속성을 유지하는 맵 투영법을 정각(正角, conformal) 또는 등각(等角, orthomorphic) 투영법 이라 합니다.

각도 관계성(angular relationship)의 유지 가 중요할 경우 이런 투영법을 사용합니다. 주로 항법 또는 기상 업무에 사용되지요. 광역에 걸쳐 진각(眞角, true angle)을 유지하는 것은 어렵기 때문에 지구의 작은 부분에서만 적용해야 한다는 점을 기억해야 합니다. 정각 유형의 투영법은 면적의 왜곡을 일으킵니다. 정각 투영으로 만들어진 맵 상에서 면적을 측정하면 정확하지 않을 것이라는 뜻이죠. 그 면적이 클수록 면적 측정의 정확도는 떨어질 것입니다. 정각 투영법의 예로는 메르카토르(Mercator) 투영법 (그림 8.5) 및 람베르트 정각 원추(Lambert Conformal Conic) 투영법 을 들 수 있습니다. 미국 지질조사국(the U.S. Geological Survey)이 만든 지형도 대부분은 정각 투영법을 사용하고 있습니다.

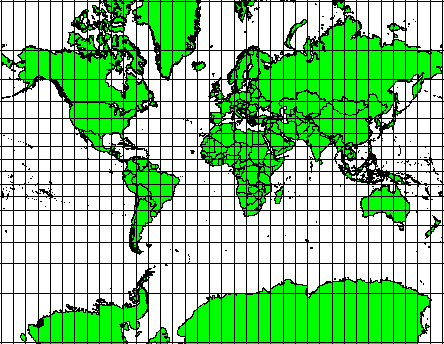
그림 8.5 메르카토르 투영법은 각도 관계성이 중요한 경우 사용되지만 면적 관계성은 왜곡됩니다.

8.4.2. 동일한 거리를 유지하는 맵 투영법

맵을 투영하는 목적이 거리를 정확하게 측정하는 것이라면, 거리를 잘 보전하도록 설계된 투영법을 선택해야 합니다. 등거리(equidistant) 투영법 이라고 하는 이런 투영법들은 맵의 축척 이 변함없이 유지 되어야 합니다. 투영의 중심으로부터 맵 상의 다른 모든 위치까지의 거리를 정확하게 나타내어야 그 맵을 등거리라고 할 수 있죠. 등거리 투영법 은 투영의 중심으로부터든 또는 어떤 선을 따라서든 정확한 거리를 유지합니다. 이런 투영법은 무선, 지진, 그리고 항법 관련 지도를 만드는 데 쓰입니다. 등거리 투영법의 훌륭한 예로는 플레이트 카레 등거리 원뿔(plate carrée equidistant cylindrical) 투영법 (그림 8.6 참조)과 등장방형(equirectangular) 투영법 이 있습니다. 정거방위(azimuthal equidistant) 투영법 은 UN 휘장(그림 8.7 참조)에 사용된 투영법입니다.

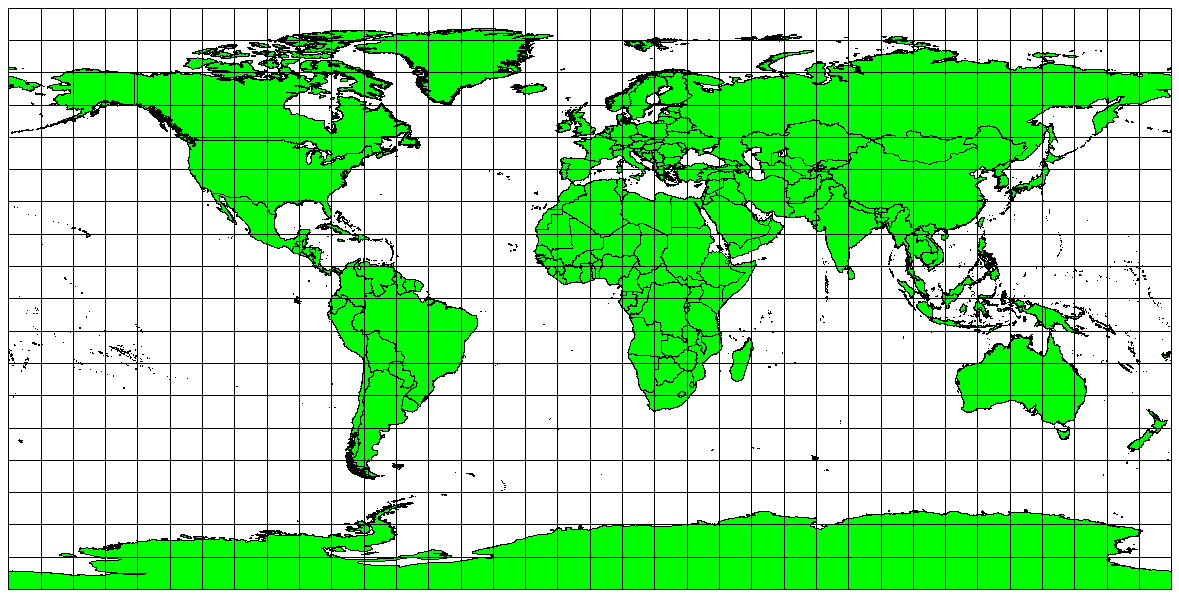
그림 8.6 거리를 정확하게 측정하는 것이 중요한 경우 등거리 투영법을, 예를 들어 플레이트 카레 등거리 원뿔 투영법을 사용합니다.

그림 8.7 UN 휘장은 정거방위 투영법을 사용합니다.

8.4.3. 동일한 면적을 유지하는 투영법

어떤 맵이 맵 전체에 걸쳐 어떤 지역들을 나타낼 때, 맵 상의 모든 지역이 해당 지역이 지구 상에서 나타내는 지역과 동일한 비율 관계를 맺고 있다면 해당 맵을 정적(正積, equal area) 맵 이라 합니다. 실생활에서 일반적인 참조 지도 및 교육용 지도들은 대부분 정적 투영법 을 사용해야 합니다. 그 이름대로, 여러분이 수행할 계산 대부분이 면적 계산일 경우 이런 맵들을 가장 잘 사용할 수 있습니다. 예를 들어 여러분이 살고 있는 도시의 특정 지역을 분석해서 해당 지역이 대형 마트를 입점시키기에 충분히 넓은지 알아보려면 정적 투영법을 사용한 지도를 선택하는 것이 가장 좋습니다. 또한 여러분이 다른 투영 유형들 대신 정적 투영법을 사용할 경우 여러분이 분석하는 지역이 넓을수록 면적 계산은 더 정확해질 것입니다. 하지만 분석 지역이 넓을수록 정적 투영법은 각도 정합의 왜곡 을 일으킬 것입니다. 정적 투영법을 사용하는 경우, 분석 지역이 좁을수록 각도가 왜곡될 가능성이 줄어듭니다. GIS 작업에서 자주 볼 수 있는 정적 투영법의 예로는 알베르스 정적(Albers equal area) 투영법, 람베르트 정적(Lambert’s equal area) 투영법 그리고 (그림 8.8 에서 볼 수 있는) 몰바이데 정적 원뿔(Mollweide equal area cylindrical) 투영법 등이 있습니다.

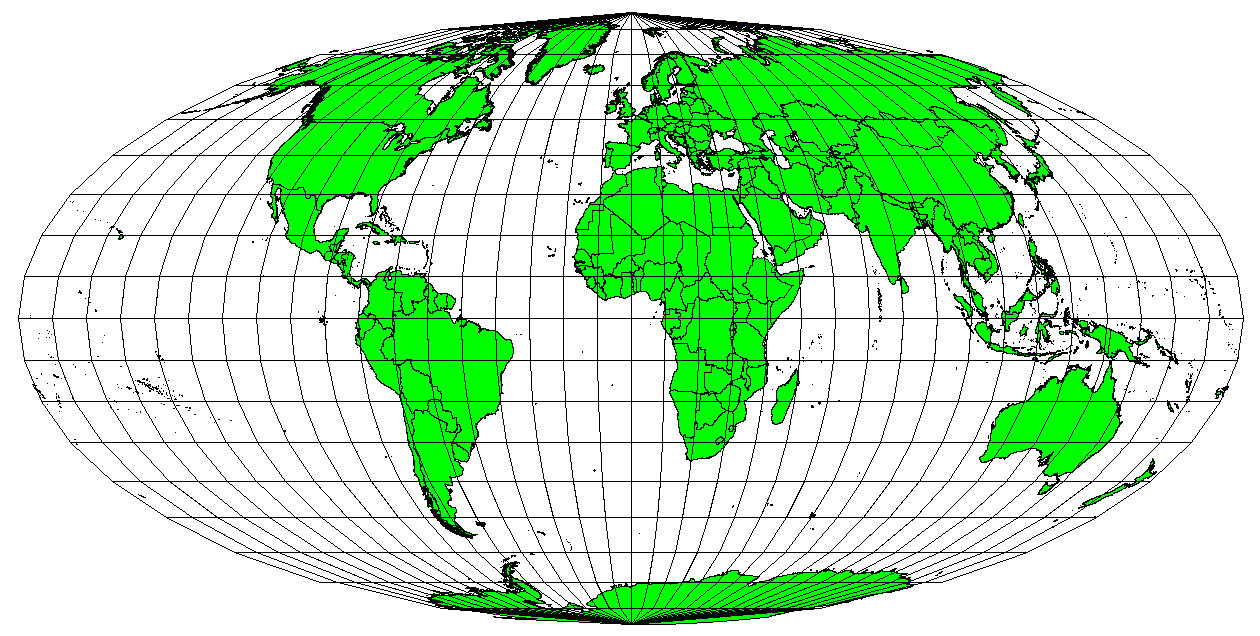
그림 8.8 정적 투영법의 한 예인 몰바이데 정적 원뿔 투영법은 맵 상의 모든 지역(면적)이 지구 상의 해당 지역(면적)과 동일한 비례 관계를 가지도록 해줍니다.

맵 투영이란 매우 복잡한 주제라는 것을 기억하십시오. 평평한 종이 한 장 위에 지구 표면의 특정 부분을 충실히 나타내려 하는 서로 다른 수많은 투영법들이 전세계에 걸쳐 존재합니다. 실제 작업 시에는 여러분이 어떤 투영법을 사용할지 결정하지는 못 할 경우가 많을 겁니다. 대부분의 국가마다 공통적으로 쓰이는 투영법을 가지고 있게 마련이고, 데이터를 교환할 때 사람들은 국가적 동향 을 따르게 될 테니까요.

8.5. 좌표계를 더 자세히

좌표계(coordinate reference system) 덕분에 지구 상의 모든 위치를 좌표라는 숫자 3개 집합으로 지정할 수 있게 되었습니다. 일반적으로 좌표계를 크게 (데카르트 좌표계 또는 직교 좌표계라고도 하는) 투영 좌표계 와 지리 좌표계 로 나눌 수 있습니다.

8.5.1. 지리 좌표계

지리 좌표계(geographic coordinate reference system)는 매우 흔히 사용됩니다. 이 좌표계는 위도(latitude)와 경도(longitude) 그리고 때로는 고도 값을 사용해서 지구 표면 상의 위치를 나타냅니다. 가장 유명한 지리 좌표계는 WGS 84 라고 합니다.

위도선(line of latitude) 은 지구를 북에서 남으로 (또는 남에서 북으로) 적도에 평행하게 균등한 간격으로 180개로 나누는 선입니다. 위도의 기준선은 적도이며 각 반구(hemisphere) 를 90개로 나눕니다. 각 위도선은 위도 1­°를 표현합니다. 북반구에서는 위도를 적도 0°부터 북극 90°로 측정합니다. 남반구의 경우 적도 0°부터 남극 90°로 측정합니다. 지도 디지타이즈 작업을 단순하게 하기 위해 남반구의 위도를 음수(0° 에서 -90°)로 할당하는 경우가 많습니다. 여러분이 지구 표면 어디에 있든, 위도선 사이의 거리는 60해리(海里)로 동일합니다. 이를 그림으로 보고 싶다면 그림 8.9 를 참조하세요.

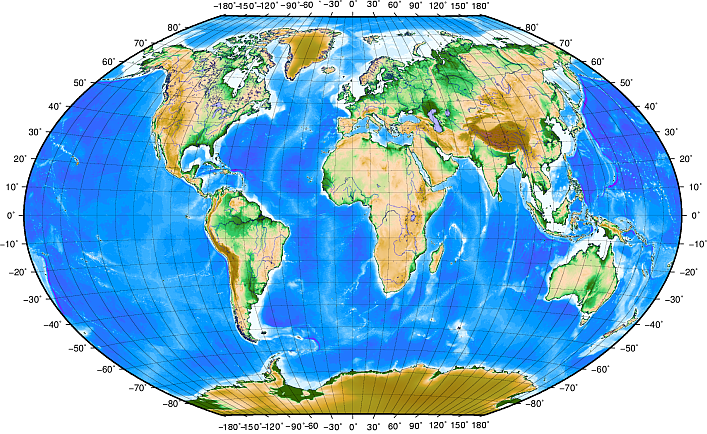
그림 8.9 적도에 평행한 위도선과 그리니치(Greenwich)를 통과하는 본초 자오선(prime meridian)에서 시작하는 경도선으로 이루어진 지리 좌표계

한편 경도선(line of longitude) 은 위도선만큼 균등성 기준을 만족시키지 못 합니다. 경도선은 적도와 직교하며 남북극을 통과합니다. 경도의 기준선(본초 자오선)은 북극에서 시작하여 영국 그리니치 시를 통과해서 남극에서 끝납니다. 그 다음 경도선들은 본초 자오선의 동쪽 또는 서쪽으로 0°에서 180°까지 측정합니다. 본초 자오선 서쪽의 값은 디지털 매핑 응용 프로그램에서 사용할 수 있기 위해 음수로 할당된다는 사실을 기억하십시오. 이를 그림으로 보고 싶다면 그림 8.9 를 참조하세요.

적도에서, 그리고 적도에서만, 경도선 하나가 표현하는 거리가 위도 1°가 표현하는 거리와 동일합니다. 남북극으로 이동할수록 경도선 사이의 거리는 점진적으로 짧아지는데, 양극의 정확한 위치에서 모든 360° 경도는 여러분의 손가락 끝으로 찍을 수 있는 한 점으로 모입니다. (물론 장갑은 끼는 게 좋겠죠.) 지리 좌표계를 사용하면 적도에서 약 12363.365km² 면적의 정사각형으로 지구를 분할하는 격자를 얻을 수 있습니다. 이것도 괜찮기는 하지만, 이 정사각형 안에 있는 객체의 위치를 구하기엔 쓸모가 별로 없는 것도 사실이죠.

솔직하게 말하자면 맵 상의 한 포인트의 위치를 (합당한 정확도 수준으로) 설명할 수 있으려면 맵 격자를 충분히 작은 부분들로 나누어야만 합니다. 이를 위해 도(°)를 분 (')과 초 (")로 나누는 것입니다. 1도는 60분이며 1분은 60초입니다. (1도가 3,600초인 것이죠.) 즉 적도 상에서 위도 또는 경도의 1초는 30.87624m가 됩니다.

8.5.2. 투영 좌표계

2차원 좌표계는 흔히 2개의 축으로 정의됩니다. 서로 직교하는 2개의 축은 XY 평면 을 구성합니다. (그림 8.10 의 왼쪽을 참조하세요.) 일반적으로 수평축을 X, 수직축을 Y 라고 합니다. 3차원 좌표계의 경우, 일반적으로 Z 라고 하는 또다른 축이 추가됩니다. 이 축도 X 와 Y 축과 직교합니다. Z 축은 3차원 공간을 생성합니다. (그림 8.10 의 오른쪽을 참조하세요.) 구형 공간의 좌표로 표현된 모든 포인트는 X Y Z 좌표로 표현될 수 있습니다.

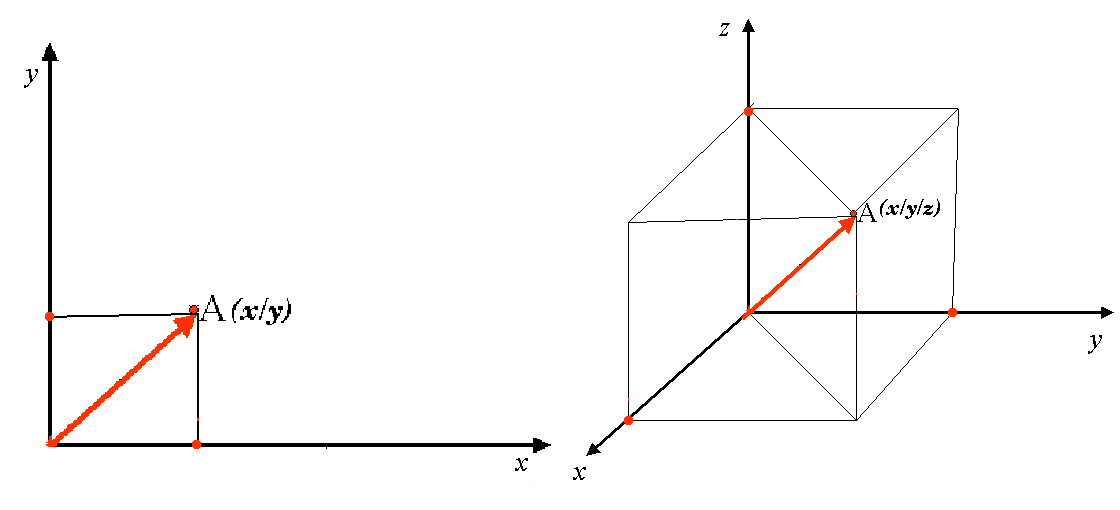
그림 8.10 2차원 좌표계와 3차원 좌표계

남반구(적도의 남쪽)의 투영 좌표계(projected coordinate reference system)는 일반적으로 적도 상의 특정 경도 를 원점으로 삼습니다. 쉽게 말하자면 남반구에서는 Y값이 남쪽으로 갈수록 증가하고 X값은 서쪽으로 갈수록 증가한다는 뜻입니다. 북반구(적도의 북쪽)의 경우에도 원점은 적도 상의 특정 경도 지만, Y값은 북쪽으로 갈수록 X값은 동쪽으로 갈수록 증가합니다. 다음 단락에서 남아프리카 공화국에서 자주 쓰이는 UTM(Universal Transverse Mercator) 좌표계라는 투영 좌표계에 대해 설명하겠습니다.

8.6. UTM 좌표계를 더 자세히

UTM(Universal Transverse Mercator) 좌표계의 원점은 적도 상의 특정 경도 입니다. 이때 Y값은 남쪽으로 갈수록 증가하고 X값은 서쪽으로 갈수록 증가합니다. UTM 좌표계는 전세계 맵 투영법입니다. 즉 지구 전체에 걸쳐 사용된다는 뜻입니다. 그러나 앞의 ‘맵 투영의 정확도’ 단락에서 설명했듯이, (예를 들어 남아프리카 같은) 넓은 지역일수록 각도 정합, 거리 및 면적의 왜곡이 나타나게 됩니다. 너무 심한 왜곡을 피하기 위해, 세계를 동쪽에서 서쪽으로 경도 6도 씩 나눈 60개의 균등 구역(equal zone) 으로 나눕니다. 이 UTM 구역들 에 반대 자오선(antimeridian) 을 시작으로 (서경 180°가 1번 구역) 동쪽으로 다시 반대 자오선 을 향해 차례대로 1에서 60까지 번호를 붙입니다. 그림 8.11 을 참조하세요.

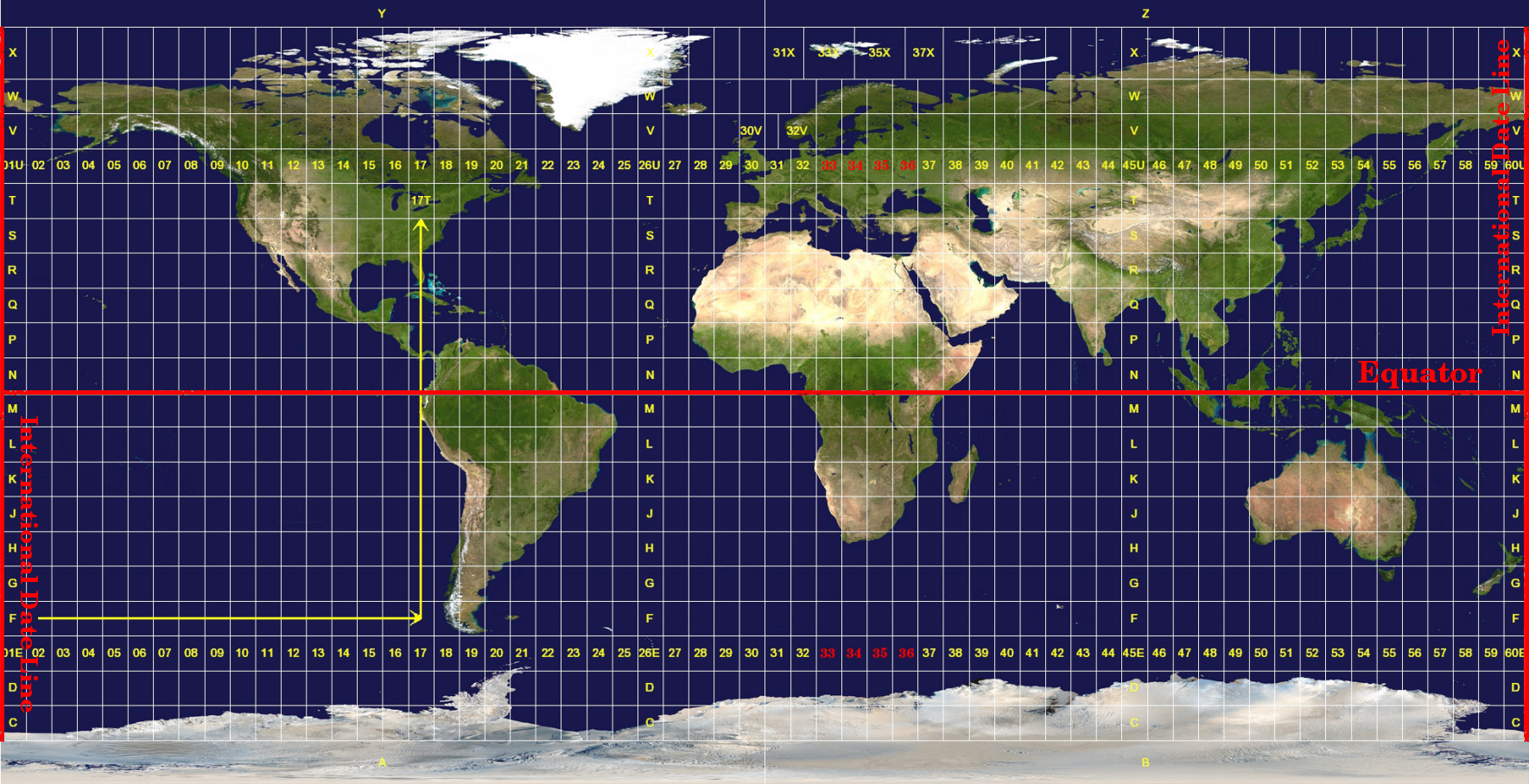
그림 8.11 UTM 구역들. 남아프리카의 경우 33S, 34S, 35S 그리고 36S UTM 구역들을 사용합니다.

그림 8.11 과 그림 8.12 를 보면 알 수 있듯이, 남아프리카 공화국은 왜곡을 최소화하기 위한 4개의 UTM 구역 으로 덮여 있습니다. 이 구역들 은 UTM 33S, UTM 34S, UTM 35S 그리고 UTM 36S 입니다. 구역 번호 뒤에 붙은 S 는 해당 UTM 구역이 남반구 에 있다는 의미입니다.

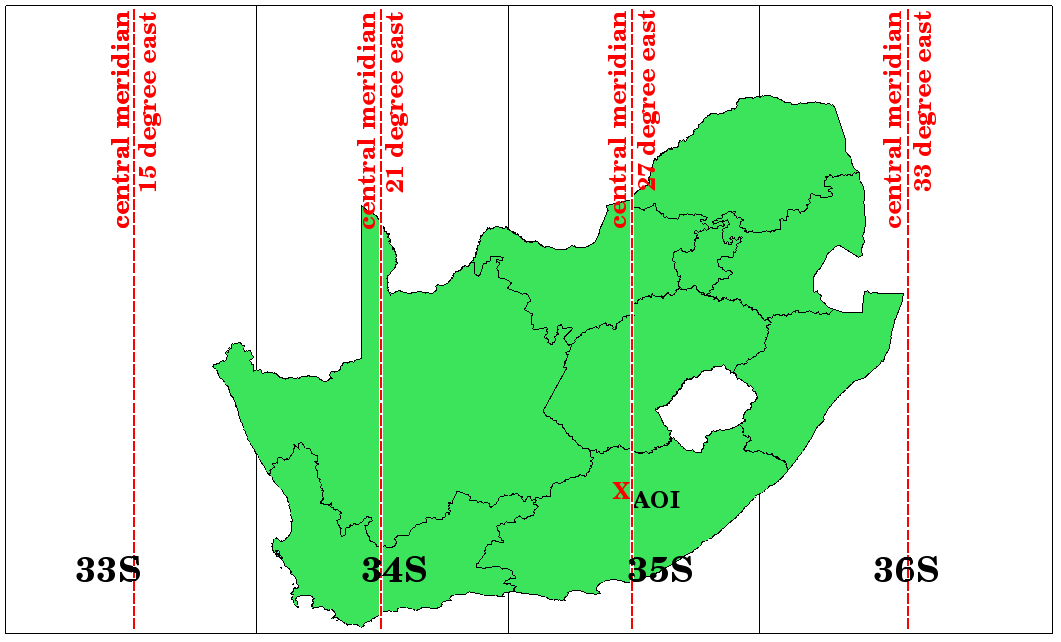
그림 8.12 남아프리카를 높은 정확도로 투영하기 위해 이용되는 33S, 34S, 35S, 및 36S UTM 구역들. 빨간 점선은 각 구역의 중심 경도(자오선)입니다. 빨간 x표는 관심 지역(Area of Interest)을 표시한 것입니다.

예를 들어서 그림 8.12 에 빨간 x표로 표시된 관심 지역(AOI) 내에 있는 2차원 좌표를 정의하려 한다고 해보죠. 해당 지역은 UTM 구역 35S 에 위치하고 있습니다. 즉 왜곡을 최소화하고 정확한 분석 결과를 얻기 위해서는 좌표계로 UTM 구역 35S 를 사용해야 합니다.

남반구 UTM 좌표의 위치는 구역 번호 (35)와 미터 단위의 편북(Y) 값 그리고 편동(X) 값 으로 표현해야만 합니다. 편북(northing) 값 이란 적도 에서부터 해당 위치까지의 거리를 미터 단위로 나타낸 값입니다. 편동(easting) 값 은 사용된 UTM 구역의 중심 자오선 (경도)에서부터 해당 위치까지의 거리를 미터 단위로 나타낸 값입니다. UTM 구역 35S의 경우 중심 경도는 그림 8.12 에서 알 수 있듯이 동경 27도 입니다. 더 자세히 설명하자면 지금 남반구를 설명하고 있는데 UTM 좌표계에서는 음수를 사용할 수 없기 때문에 편북(Y) 값에 가짜 편북 값(false northing value) 10,000,000m를 더해주고 편동(X) 값에 가짜 편동 값 500,000m를 더해줘야 합니다. 어려운 것 같지요. 그러면 관심 지역 의 정확한 UTM 35S 좌표를 찾는 방법을 보여주는 예제를 풀어보겠습니다.

8.6.1. 편북(Y) 값

우리가 찾는 위치는 적도에서 남쪽으로 3,550,000m 거리이므로 편북(Y) 값은 음의 부호 이며 -3,550,000m가 되는데, UTM 정의에 따라 가짜 편북 값 10,000,000m를 더해야 합니다. 따라서 해당 위치 좌표의 편북(Y) 값은 6,450,000m(-3,550,000m + 10,000,000m)입니다.

8.6.2. 편동(X) 값

먼저 UTM 구역 35S 의 중심 자오선 (경도)를 찾아야 하는데, 그림 8.12 를 보면 알 수 있듯이 동경 27도 입니다. 우리가 찾는 위치는 중심 자오선에서 서쪽으로 85,000m 입니다. 편북 값과 마찬가지로 편동(X) 값에도 음의 부호가 붙기 때문에 -85,000m 가 되는데 여기에 UTM 정의에 따라 가짜 편동 값 500,000m를 더해야 합니다. 즉 우리가 찾는 위치 좌표의 편동(X) 값은 415,000m(-85,000m + 500,000m)입니다. 마지막으로 정확한 값을 얻으려면 이 편동 값에 구역 번호 를 붙여야 합니다.

따라서 우리가 찾는, UTM 구역 35S 로 투영된 관심 지역 의 좌표는 35 415,000m E / 6,450,000m N 이라고 표기될 것입니다. 일부 GIS에서는 시스템 내에서 UTM 구역 35S을 정확하게 정의하고 단위를 미터로 설정한 경우, 이 좌표를 간단하게 415,000 6,450,000 이라고 표시할 수도 있습니다.

8.7. 실시간(On-The-Fly) 투영

아마 여러분도 상상이 되겠지만, 여러분이 GIS에서 사용하고 싶은 데이터가 다른 좌표계로 투영돼 있을 수도 있습니다. 예를 들어 남아프리카 공화국의 국경을 UTM 35S로 투영한 벡터 레이어가 있는데, 강수량에 관한 정보를 담고 있는 포인트 벡터 레이어는 지리 좌표계인 WGS 84로 투영되어 있는 경우 말이죠. GIS에서는 이 두 벡터 레이어가 맵 창에서 완전히 서로 다른 영역에 표시됩니다. 두 벡터 레이어의 투영법이 다르기 때문입니다.

이 문제를 해결하기 위해, GIS 대다수는 실시간(on-the-fly) 투영이라는 기능을 포함하고 있습니다. 즉 GIS를 구동할 때 특정 투영법을 정의 하면, 그 다음 여러분이 불러오는 모든 레이어는 – 어떤 좌표계로 투영되었든 상관없이 – 자동적으로 여러분이 정의한 투영법으로 표시될 것이라는 뜻입니다. 이 기능을 통해 GIS의 맵 창 안에 서로 다른 좌표계로 투영돼 있을 수도 있는 레이어들을 중첩시킬 수 있습니다. QGIS는 이 기능을 기본적으로 활성화시켜 놓고 있습니다.

8.8. 공통적으로 조심해야 할 문제들/사항들

맵 투영 이라는 문제는 매우 복잡하기 때문에 지리학, 측지학 또는 다른 GIS 관련 과학을 공부한 전문가라 할지라도 맵 투영 및 좌표계의 정확한 정의를 내리는 데 곤란을 겪는 경우가 많습니다. 일반적으로 GIS 작업 시, 처음부터 투영된 데이터를 이용하게 될 겁니다. 대부분의 경우 이런 데이터는 특정 좌표계로 투영될 것이기 때문에 여러분이 새 좌표계를 만들거나, 데이터를 어떤 좌표계에서 다른 좌표계로 재투영할 필요는 없습니다. 그렇기는 하지만, 맵 투영이 어떤 것인지 그리고 좌표계의 의미란 무엇인지에 대해 알고 있는 것이 유용할 겁니다.

8.9. 무엇을 배웠나요?

이제 이번 단원에서 배운 내용을 정리해볼까요:

• 맵 투영 이란 지구 표면을 2차원의 평평한 종이 또는 컴퓨터 스크린 위에 묘사하는 작업입니다.

• 전세계 맵 투영법도 존재하지만, 대부분의 맵 투영법은 지구 표면의 좁은 지역을 투영하기 위해 최적화 되도록 생성되었습니다.

• 맵 투영은 절대로 구형인 지구를 완전하고 정확하게 표현할 수 없습니다. 맵 투영은 각도 정합, 거리, 면적을 왜곡 시킵니다. 맵 투영 시 이 모든 특성을 동시에 보전할 수는 없습니다.

• 좌표계(CRS) 는 좌표를 통해 2차원의 투영된 맵이 어떻게 지구 상의 실재 위치와 연결되는지를 정의합니다.

• 좌표계에는 서로 다른 두 가지 유형이 있습니다: 지리 좌표계 와 투영 좌표계 입니다.

• 실시간 투영은 GIS의 기능으로 레이어들이 서로 다른 좌표계로 투영돼 있더라도 해당 레이어들을 중첩시킬 수 있게 해줍니다.

8.10. 도전해봅시다!

강사와 학생들이 함께 시도해볼 만한 몇 가지 아이디어가 있습니다:

1. QGIS를 시작하십시오.

2. Project ► Properties… ► CRS 메뉴에서 No projection (or unknown/non-Earth projection) 옵션을 체크하십시오.

3. 동일한 지역이지만 서로 다른 투영법을 사용한 레이어 2개를 불러오십시오.

4. 학생들에게 두 레이어에 있는 몇몇 위치의 좌표를 찾아보게 하십시오. 두 레이어를 중첩시킬 수 없다는 사실을 보여주면 됩니다.

5. 그 다음 Project Properties 대화창에서 좌표계를 Geographic/WGS 84로 정의하십시오.

6. 동일 지역의 두 레이어를 불러와서 학생들에게 프로젝트 용 좌표계를 설정하면 (즉 “실시간” 투영을 활성화하면) 어떤 일이 일어나는지 보여주세요.

7. QGIS의 Project Properties 대화창을 열어서 학생들에게 서로 다른 좌표계들이 얼마나 많은지, 따라서 좌표계라는 주제가 얼마나 복잡한지 알려주십시오. 서로 다른 좌표계를 선택해서 동일한 레이어를 서로 다른 투영법으로 표시해주어도 됩니다.

8.11. 생각해볼 점

사용할 수 있는 컴퓨터가 없을 경우, 학생들에게 맵 투영법 삼족의 원칙을 알려줄 수 있습니다. 지구본과 종이를 준비해서 원통형, 원뿔형 그리고 평면 투영법이 일반적으로 각각 어떻게 작동하는지 실연해 보이십시오. 투명지를 사용해서 X축과 Y축을 보여주는 2차원 좌표계를 그릴 수도 있습니다. 그 다음 학생들에게 서로 다른 위치를 나타내는 좌표(X 및 Y 값)를 정의하도록 해보십시오.

8.12. 더 읽어볼 거리

서적:

• Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986

• DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195

• Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X

웹사이트:

• https://foote.geography.uconn.edu/gcraft/notes/mapproj/mapproj_f.html

• http://geology.isu.edu/wapi/geostac/Field_Exercise/topomaps/index.htm

QGIS 사용자 지침서도 QGIS에서 어떻게 맵 투영 작업을 하는지에 대한 보다 상세한 정보를 수록하고 있습니다.

8.13. 다음 단원은?

다음 단원에서 우리는 지도 생산 에 대해 자세히 살펴볼 것입니다.