Viktigt

Översättning är en gemenskapsinsats du kan gå med i. Den här sidan är för närvarande översatt till 100.00%.

3. Vektordata

	Mål:	Förståelse för vektordatamodeller som används i GIS.
	Nyckelord:	Vektor, punkt, polylinje, polygon, vertex, geometri, skala, datakvalitet, symbologi, datakällor

3.1. Översikt

** Vektordata** är ett sätt att representera verkliga funktioner i GIS-miljön. En funktion är något som du kan se i landskapet. Föreställ dig att du står på toppen av en kulle. När du tittar nedåt kan du se hus, vägar, träd, floder och så vidare (se Fig. 3.30). Var och en av dessa saker skulle vara en feature när vi representerar dem i en GIS-applikation. Vektorobjekt har attribut, som består av text eller numerisk information som beskriver objekten.

Fig. 3.30 När du tittar på ett landskap kan du se huvuddragen, t.ex. vägar, hus och träd.

En vektorfunktion har sin form representerad med hjälp av geometri. Geometrin består av en eller flera sammankopplade vertices. En vertex beskriver en position i rummet med hjälp av en X-, Y- och eventuellt Z-axel. Geometrier som har vertex med en Z-axel kallas ofta 2,5D eftersom de beskriver höjd eller djup vid varje vertex, men inte både och.

När en funktions geometri består av endast en enda vertex kallas den en punkt-funktion (se illustration Fig. 3.31). Om geometrin består av två eller flera hörn och det första och sista hörnet inte är lika, bildas en polyline-funktion (se illustration Fig. 3.32). Om det finns tre eller fler hörn och det sista hörnet är lika med det första, bildas en sluten polygon (se illustration Fig. 3.33).

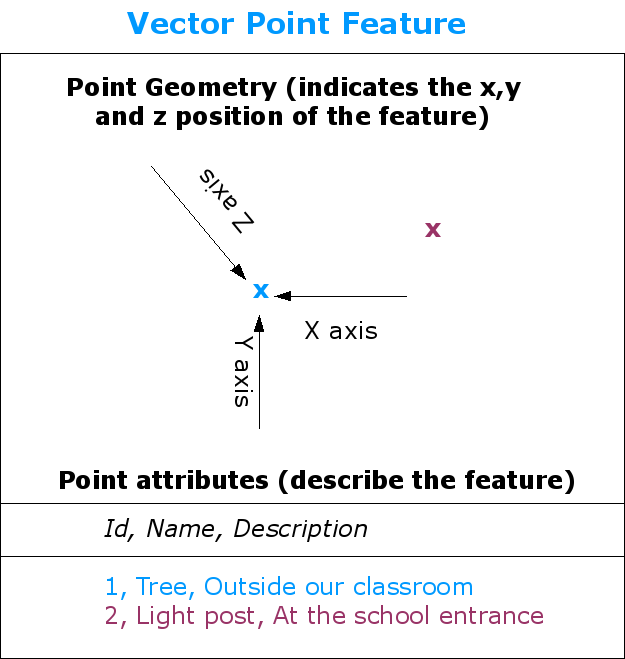
Fig. 3.31 En punkt beskrivs av dess X-, Y- och eventuellt Z-koordinat. Punktattributen beskriver punkten, t.ex. om det är ett träd eller en lyktstolpe.

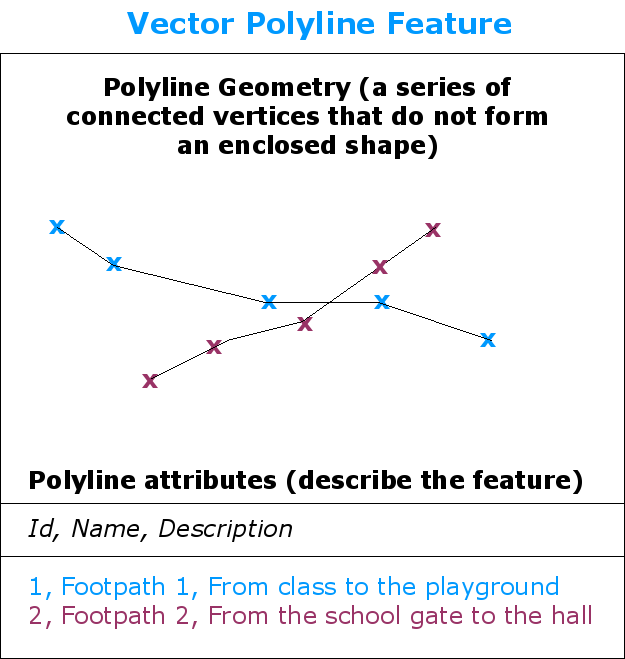
Fig. 3.32 En polylinje är en sekvens av sammanfogade hörnpunkter. Varje hörnpunkt har en X-, Y- (och eventuellt Z-) koordinat. Attribut beskriver polylinjen.

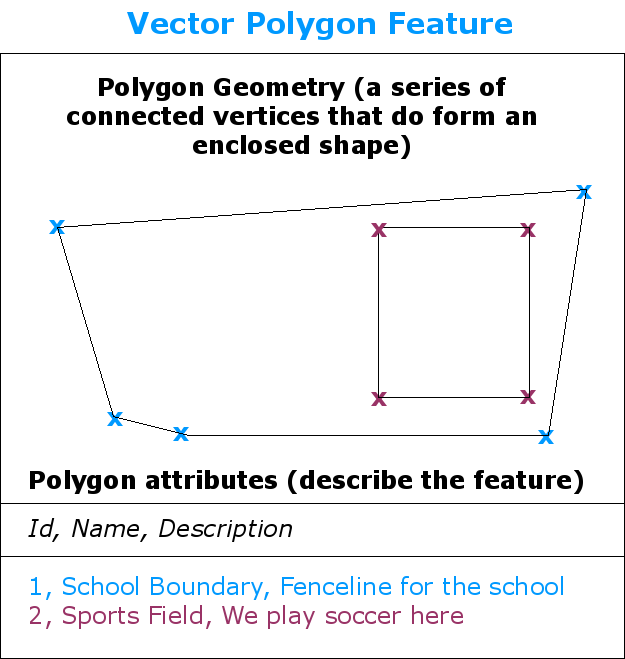
Fig. 3.33 En polygon är, precis som en polylinje, en sekvens av hörnpunkter. I en polygon är dock den första och den sista hörnpunkten alltid på samma plats.

Om du tittar tillbaka på bilden av ett landskap som vi visade dig längre upp bör du kunna se de olika typerna av funktioner på det sätt som ett GIS representerar dem nu (se illustration Fig. 3.34).

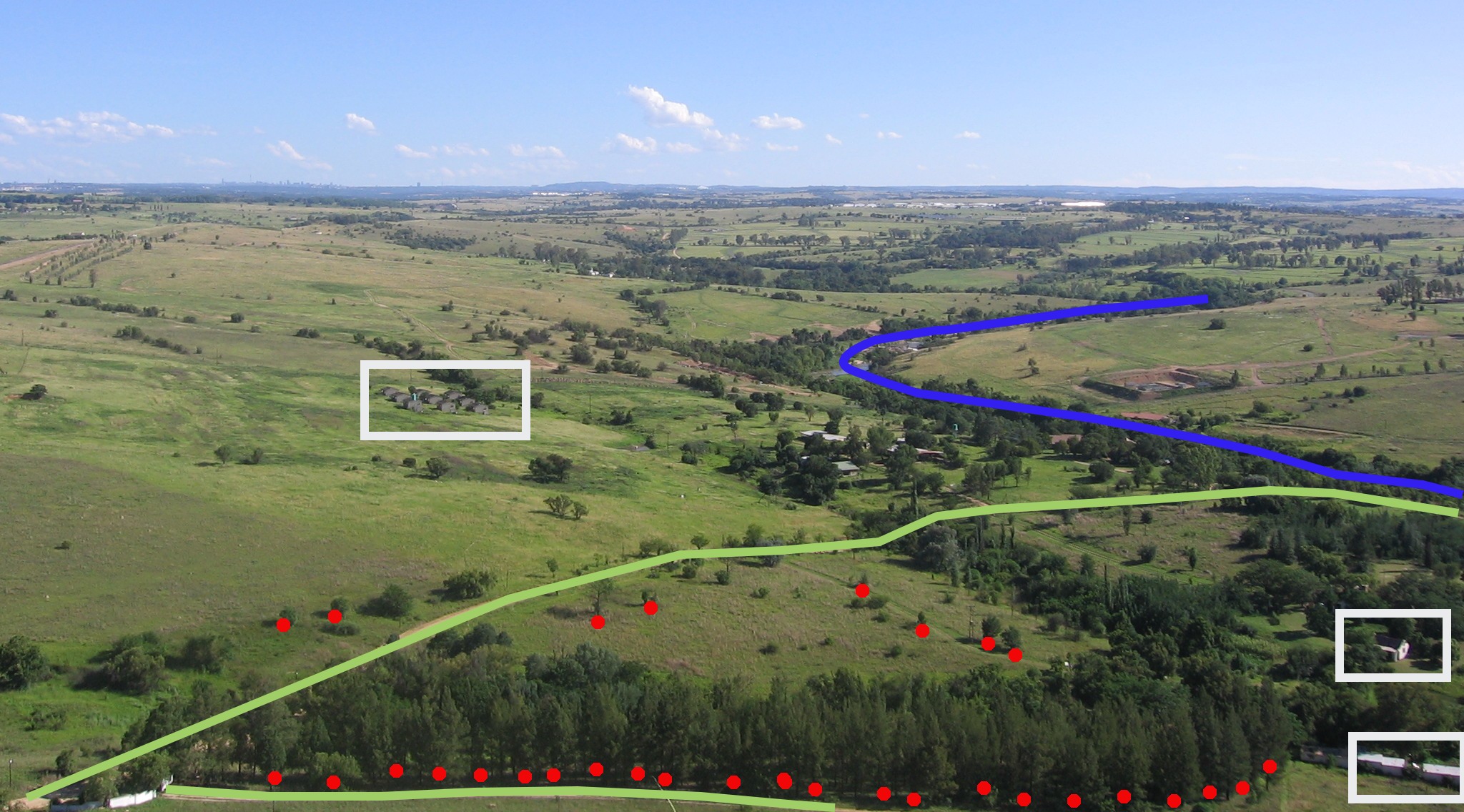
Fig. 3.34 Landskapselement så som vi skulle presentera dem i ett GIS. Floder (blå) och vägar (gröna) kan representeras som linjer, träd som punkter (röda) och hus som polygoner (vita).

3.2. Punktfunktioner i detalj

Det första vi måste inse när vi talar om punktfunktioner är att vad vi beskriver som en punkt i GIS är en fråga om åsikt och ofta beroende av skala. låt oss titta på städer till exempel. Om du har en småskalig karta (som täcker ett stort område) kan det vara vettigt att representera en stad med hjälp av en punktfunktion. Men när du zoomar in på kartan och rör dig mot en större skala är det mer meningsfullt att visa stadsgränserna som en polygon.

När du väljer att använda punkter för att representera en funktion är mest en fråga om skala (hur långt bort är du från funktionen), bekvämlighet (det tar mindre tid och ansträngning att skapa punktfunktioner än polygonfunktioner) och typen av funktion (vissa saker som telefonstolpar är helt enkelt inte meningsfulla att lagra som polygoner).

Som vi visar i illustrationen Fig. 3.31 har en punktfunktion ett X-, Y- och eventuellt Z-värde. X- och Y-värdena beror på vilket koordinatreferenssystem (CRS) som används. Vi kommer att gå in mer i detalj på koordinatreferenssystem i en senare handledning. För tillfället kan vi helt enkelt säga att ett CRS är ett sätt att exakt beskriva var en viss plats befinner sig på jordens yta. Ett av de vanligaste referenssystemen är Longitud och Latitud. Longitudlinjerna går från nordpolen till sydpolen. Latitudlinjerna går från öst till väst. Du kan beskriva exakt var du befinner dig på vilken plats som helst på jorden genom att ange din longitud (X) och latitud (Y). Om du gör en liknande mätning för ett träd eller en telefonstolpe och markerar det på en karta, har du skapat en punktfunktion.

Eftersom vi vet att jorden inte är platt är det ofta användbart att lägga till ett Z-värde till en punktfunktion. Detta beskriver hur högt över havet du befinner dig.

3.3. Polylinjefunktioner i detalj

Där en punktfunktion är ett enda vertex, har en polylinje två eller flera vertex. Polylinjen är en kontinuerlig bana som dras genom varje vertex, vilket visas i Fig. 3.32. När två hörn sammanfogas skapas en linje. När fler än två är sammanfogade bildar de en ”linje av linjer”, eller polylinje.

En polylinje används för att visa geometrin för linjära funktioner som vägar, floder, konturer, gångstigar, flygvägar och så vidare. Ibland har vi särskilda regler för polylinjer utöver deras grundläggande geometri. Konturlinjer kan t.ex. beröra varandra (t.ex. vid en klippvägg) men får aldrig korsa varandra. På samma sätt bör polylinjer som används för att lagra ett vägnät vara anslutna vid korsningar. I vissa GIS-applikationer kan du ställa in dessa specialregler för en objekttyp (t.ex. vägar) och GIS kommer då att se till att dessa polylinjer alltid följer dessa regler.

Om en krökt polylinje har mycket stora avstånd mellan hörnen kan den se vinkelformad eller ojämn ut, beroende på i vilken skala den betraktas (se Fig. 3.35). På grund av detta är det viktigt att polylinjer digitaliseras (fångas in i datorn) med avstånd mellan hörn som är tillräckligt små för den skala som du vill använda data på.

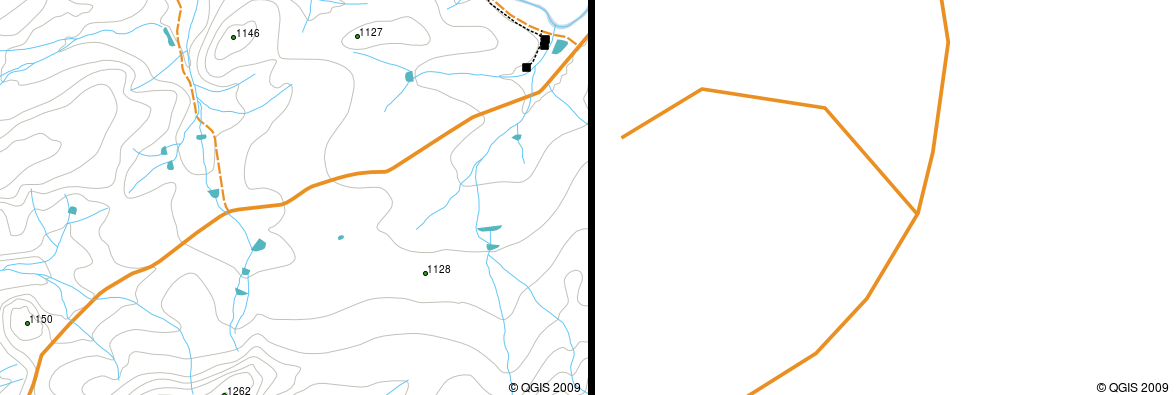
Fig. 3.35 Polylinjer som betraktas i mindre skala (1:20 000 till vänster) kan se släta och böjda ut. När du zoomar in till en större skala (1:500 till höger) kan polylinjerna se mycket kantiga ut.

En polylines attribut beskriver dess egenskaper eller kännetecken. En vägpolylinje kan t.ex. ha attribut som beskriver om den är belagd med grus eller tjära, hur många körfält den har, om den är enkelriktad och så vidare. GIS kan använda dessa attribut för att symbolisera polylinjeobjektet med en lämplig färg eller linjestil.

3.4. Polygonfunktioner i detalj

Polygonelement är omslutna områden som dammar, öar, landsgränser och så vidare. Precis som polyline-objekt skapas polygoner av en serie hörnpunkter som är förbundna med en kontinuerlig linje. Men eftersom en polygon alltid beskriver ett slutet område måste det första och sista hörnet alltid vara på samma plats! Polygoner har ofta delad geometri — gränser som är gemensamma med en angränsande polygon. Många GIS-applikationer har möjlighet att se till att gränserna för närliggande polygoner sammanfaller exakt. Vi kommer att utforska detta i ämnet Topologi senare i denna handledning.

Precis som med punkter och polylinjer har polygoner attribut. Attributen beskriver varje polygon. En damm kan t.ex. ha attribut för djup och vattenkvalitet.

3.5. Vektordata i lager

Nu när vi har beskrivit vad vektordata är ska vi titta på hur vektordata hanteras och används i en GIS-miljö. De flesta GIS-applikationer grupperar vektorfunktioner i lager. Objekten i ett lager har samma geometrityp (t.ex. är alla punkter) och samma typ av attribut (t.ex. information om vilken art ett träd är för ett trädlager). Om du t.ex. har registrerat positionerna för alla gångvägar i din skola, lagras de vanligtvis tillsammans på datorns hårddisk och visas i GIS som ett enda lager. Det här är praktiskt eftersom du då kan dölja eller visa alla funktioner för det lagret i GIS-programmet med ett enda musklick.

3.6. Redigera vektordata

GIS-programmet tillåter dig att skapa och ändra geometridata i ett lager — en process som kallas digitalisering — som vi kommer att titta närmare på i en senare handledning. Om ett lager innehåller polygoner (t.ex. jordbruksdammar), tillåter GIS-programmet endast att du skapar nya polygoner i det lagret. På samma sätt gäller att om du vill ändra formen på en funktion, tillåter programmet dig bara att göra det om den ändrade formen är korrekt. Det går t.ex. inte att redigera en linje så att den bara har ett toppunkt — kom ihåg att alla linjer måste ha minst två toppunkter, vilket vi diskuterade i avsnittet om linjer ovan.

Att skapa och redigera vektordata är en viktig funktion i ett GIS eftersom det är ett av de viktigaste sätten att skapa personliga data för saker som du är intresserad av. Säg till exempel att du övervakar föroreningar i en flod. Du kan använda GIS för att digitalisera alla utlopp för dagvattenledningar (som punktobjekt). Du kan också digitalisera själva floden (som en polylinjefunktion). Slutligen kan du göra mätningar av pH-värden längs floden och digitalisera de platser där du gjort dessa mätningar (som ett punktlager).

Förutom att du kan skapa dina egna data finns det en hel del gratis vektordata som du kan få och använda. Du kan till exempel hämta vektordata som visas på kartbladen 1:50 000 från Chief Directorate: Undersökningar och kartläggning.

3.7. Skal- och vektordata

Kartans skala är en viktig fråga att ta hänsyn till när man arbetar med vektordata i ett GIS. När data samlas in digitaliseras de vanligtvis från befintliga kartor eller genom att information hämtas från lantmäteriakter och enheter för globala positioneringssystem. Kartor har olika skalor, så om du importerar vektordata från en karta till en GIS-miljö (t.ex. genom att digitalisera papperskartor) kommer de digitala vektordata att ha samma skalproblem som originalkartan. Denna effekt kan ses i illustrationerna Fig. 3.36 och Fig. 3.37. Många problem kan uppstå om man gör ett dåligt val av kartskala. Om man t.ex. använder vektordata i illustrationen Fig. 3.36 för att planera ett våtmarksskyddsområde kan det leda till att viktiga delar av våtmarken lämnas utanför reservatet! Om du å andra sidan försöker skapa en regional karta kan det vara helt okej att använda data som samlats in i skala 1:1000 000, vilket sparar dig mycket tid och ansträngning när du samlar in data.

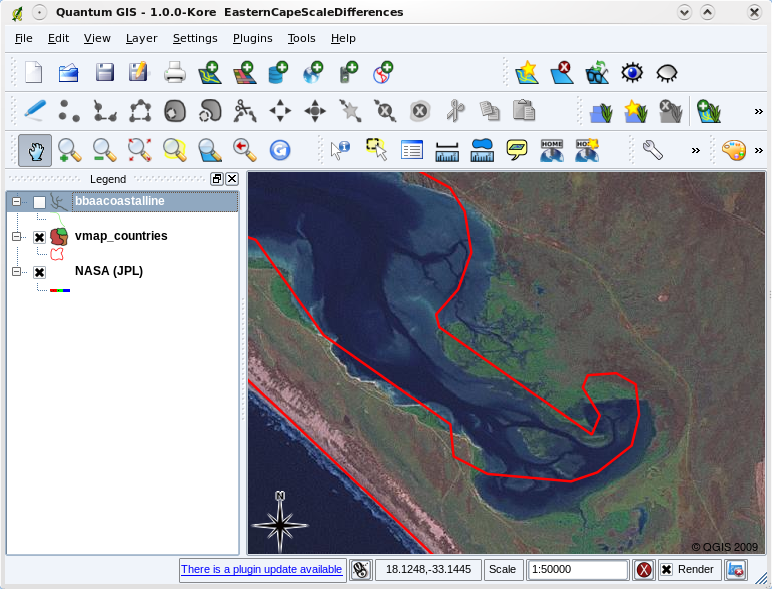
Fig. 3.36 Vektordata (röda linjer) som digitaliserades från en småskalig karta (1:1000 000).

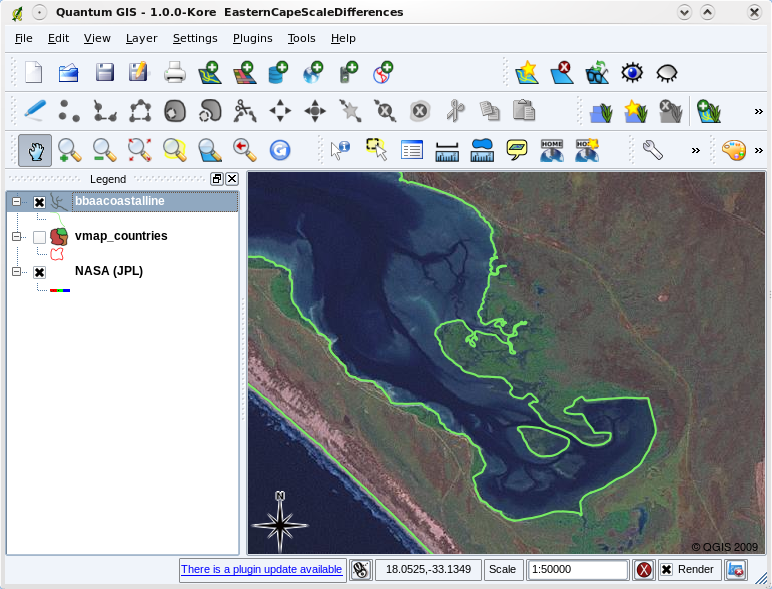
Fig. 3.37 Vektordata (gröna linjer) som digitaliserades från en storskalig karta (1:50 000).

3.8. Symbologi

När du lägger till vektorlager i kartvyn i ett GIS-program ritas de med slumpmässiga färger och enkla symboler. En av de stora fördelarna med att använda ett GIS är att du mycket enkelt kan skapa personliga kartor. I GIS-programmet kan du välja färger som passar till funktionstypen (du kan t.ex. be programmet att rita ett vektorlager med vattendrag i blått). GIS låter dig också justera den symbol som används. Så om du har ett trädpunktsskikt kan du visa varje trädposition med en liten bild av ett träd, i stället för den grundläggande cirkelmarkören som GIS använder när du först laddar lagret (se illustrationerna Fig. 3.38, Fig. 3.39 och Fig. 3.40).

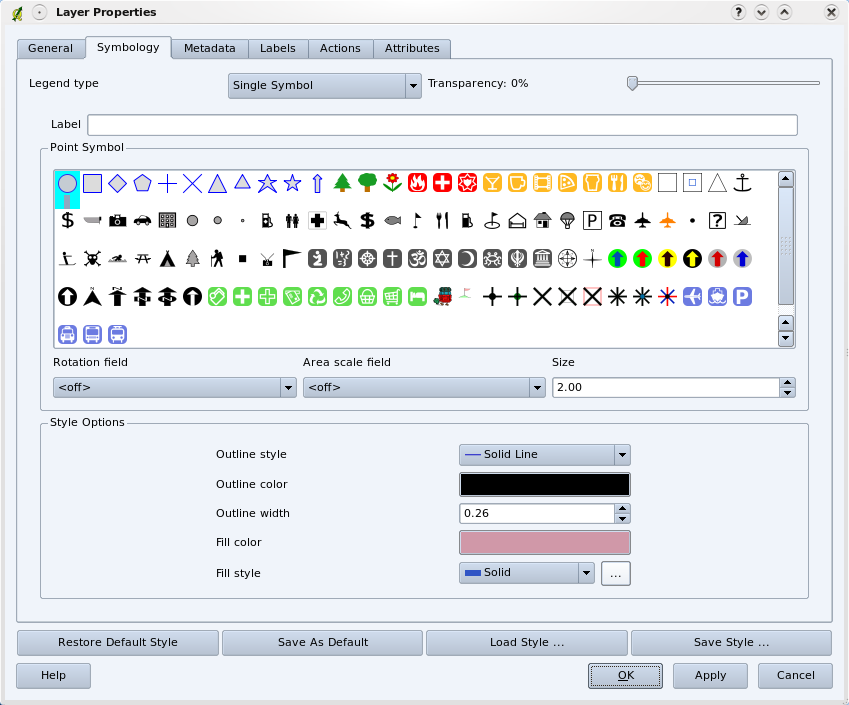
Fig. 3.38 I GIS kan du använda en panel (som den ovan) för att justera hur funktioner i ditt lager ska ritas.

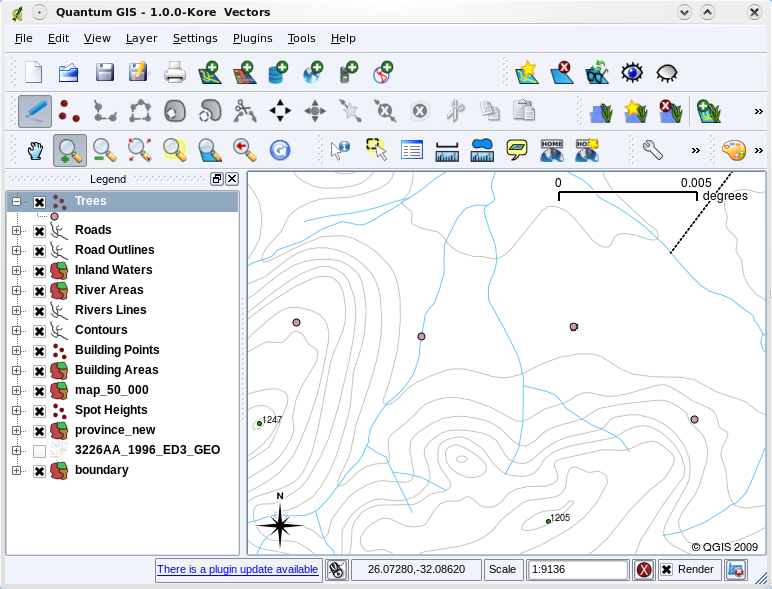
Fig. 3.39 När ett lager (t.ex. trädlagret ovan) laddas första gången kommer ett GIS-program att ge det en generisk symbol.

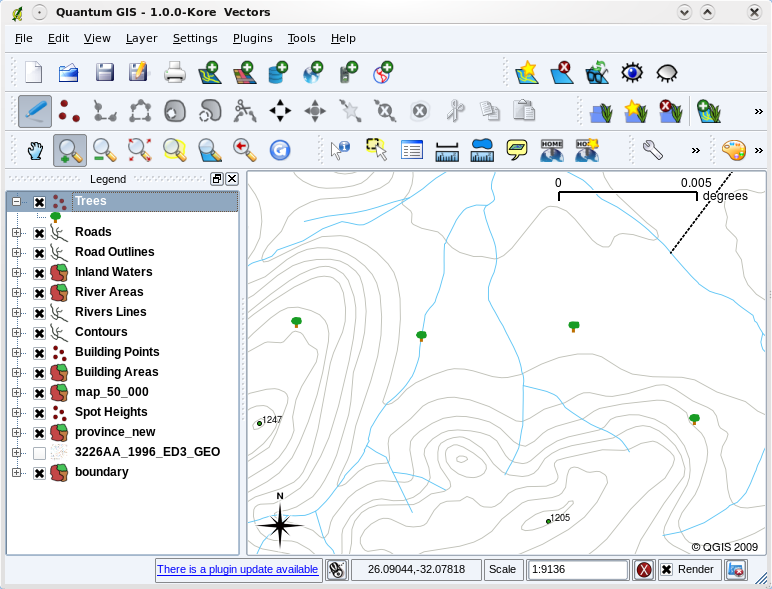
Fig. 3.40 När vi har gjort våra justeringar är det mycket lättare att se att våra punkter representerar träd.

Symbologi är en kraftfull funktion som ger liv åt kartor och gör det lättare att förstå data i ditt GIS. I följande ämne (Vektorattributdata) kommer vi att gå djupare in på hur symbologi kan hjälpa användaren att förstå vektordata.

3.9. Vad kan vi göra med vektordata i ett GIS?

På den enklaste nivån kan vi använda vektordata i en GIS-applikation på ungefär samma sätt som du skulle använda en vanlig topografisk karta. Den verkliga kraften i GIS börjar visa sig när man börjar ställa frågor som ”vilka hus ligger inom 100-årsflödet i en flod?”; ”var är det bästa stället att placera ett sjukhus så att det är lättillgängligt för så många människor som möjligt?”; ”vilka elever bor i en viss förort?”. Ett GIS är ett utmärkt verktyg för att besvara den här typen av frågor med hjälp av vektordata. I allmänhet kallar vi processen för att besvara den här typen av frågor för spatial analys. I senare delar av denna handledning kommer vi att titta närmare på spatial analys.

3.10. Vanliga problem med vektordata

Att arbeta med vektordata innebär vissa problem. Vi har redan nämnt de problem som kan uppstå med vektorer som fångats i olika skalor. Vektordata kräver också mycket arbete och underhåll för att de ska vara korrekta och tillförlitliga. Felaktiga vektordata kan uppstå när de instrument som används för att samla in data inte är korrekt inställda, när de personer som samlar in data inte är försiktiga, när tid eller pengar inte räcker till för att samla in tillräckligt med detaljer, och så vidare.

Om du har vektordata av dålig kvalitet kan du ofta upptäcka detta när du tittar på data i ett GIS. Till exempel kan slivers uppstå när kanterna på två polygonområden inte möts ordentligt (se Fig. 3.41).

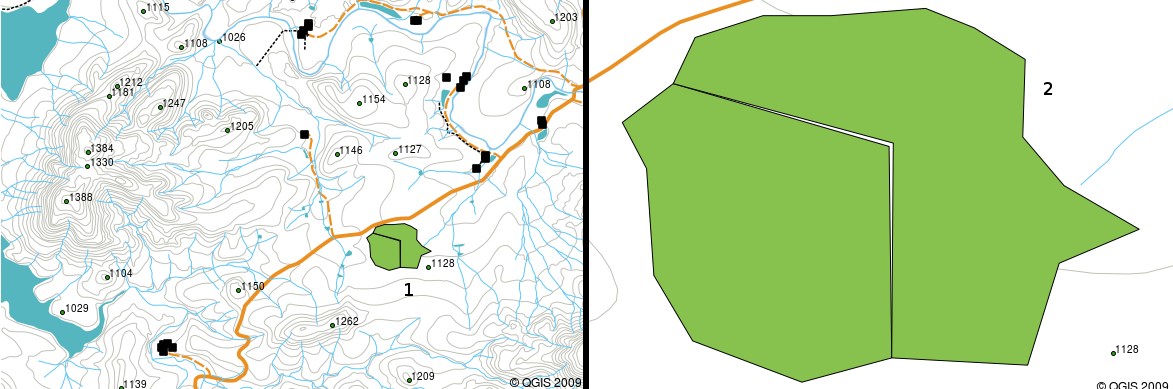
Fig. 3.41 Slivers uppstår när hörnen på två polygoner inte matchar varandra på deras kanter. I liten skala (t.ex. 1 till vänster) är det inte säkert att du kan se dessa fel. I stor skala syns de som tunna remsor mellan två polygoner (2 till höger).

Overshoots kan uppstå när en linjefunktion, t.ex. en väg, inte möter en annan väg exakt i en korsning. Undershoots kan uppstå när en linjefunktion (t.ex. en flod) inte exakt möter en annan funktion som den ska anslutas till. Figur Fig. 3.42 visar hur underskott och överskott ser ut.

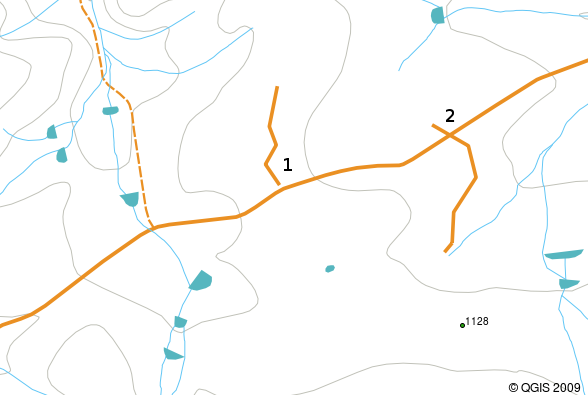
Fig. 3.42 Undershoots (1) uppstår när digitaliserade vektorlinjer som ska ansluta till varandra inte riktigt rör vid varandra. Overshoots (2) inträffar om en linje slutar bortom den linje som den ska ansluta till.

På grund av dessa typer av fel är det mycket viktigt att digitalisera data noggrant och exakt. I det kommande ämnet om topologi kommer vi att undersöka några av dessa typer av fel mer i detalj.

3.11. Vad har vi lärt oss?

Låt oss sammanfatta vad vi behandlat i det här arbetsbladet:

• ** Vektordata** används för att representera verkliga funktioner i ett GIS.

• En vektorfunktion kan ha en geometri av typen punkt, linje eller en polygon.

• Varje vektorfunktion har attributdata som beskriver den.

• Objektets geometri beskrivs i termer av vertices.

• Punktgeometrier består av ett enkelt vertex (X, Y och eventuellt Z).

• Polylinjegeometrier består av två eller fler hörnpunkter som bildar en sammanhängande linje.

• Polygongeometrier består av minst fyra hörn som bildar ett omslutet område. Det första och sista hörnet är alltid på samma plats.

• Vilken geometrityp som ska användas beror på skala, bekvämlighet och vad du vill göra med data i GIS.

• De flesta GIS-program tillåter inte att man blandar mer än en geometrityp i ett och samma lager.

• Digitalisering är en process där man skapar digitala vektordata genom att rita dem i en GIS-applikation.

• Vektordata kan ha kvalitetsproblem som underskott, överskott och slivers som du måste vara medveten om.

• Vektordata kan användas för spatial analys i ett GIS-program, t.ex. för att hitta närmaste sjukhus till en skola.

Vi har sammanfattat GIS-vektordatakonceptet i figur Fig. 3.43.

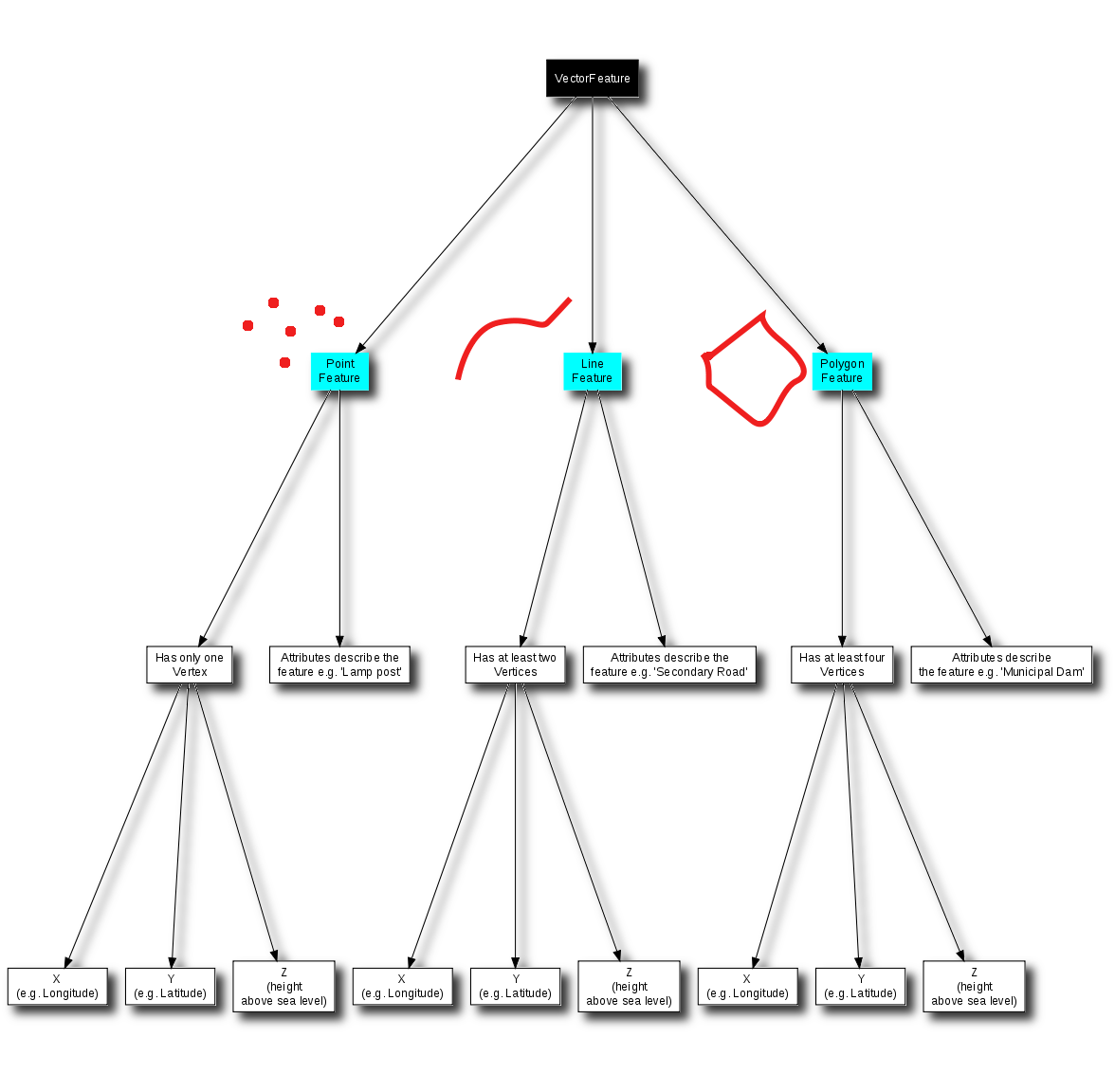
Fig. 3.43 Detta diagram visar hur GIS-applikationer hanterar vektordata.

3.12. Nu får du försöka!

Här är några idéer som du kan prova med dina elever:

• Använd en kopia av en toposheet-karta för ditt lokala område (som den som visas i Fig. 3.44) och se om dina elever kan identifiera exempel på de olika typerna av vektordata genom att markera dem på kartan.

• Fundera på hur du skulle skapa vektorfunktioner i ett GIS för att representera verkliga funktioner på din skolgård. Skapa en tabell över olika funktioner i och runt din skola och låt sedan eleverna avgöra om de bäst representeras i GIS som en punkt, linje eller polygon. Se tabell_vektor_1 för ett exempel.

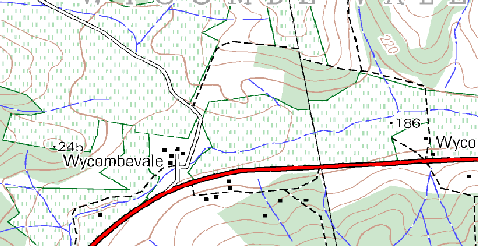
Fig. 3.44 Kan du identifiera två punktobjekt och ett polygonobjekt på den här kartan?

Funktion i den verkliga världen	Lämplig geometrityp
Skolans flaggstång
Fotbollsplanen
Gångstigarna i och runt skolan
Platser där kranar är placerade
Och så vidare.

Tabell Vektor 1: Skapa en tabell som denna (lämna kolumnen för geometrityp tom) och be dina elever att besluta om lämpliga geometrityper.

3.13. Något att tänka på

Om du inte har en dator tillgänglig kan du använda ett toposark och transparensark för att visa dina elever om vektordata.

3.14. Ytterligare läsning

QGIS User Guide innehåller också mer detaljerad information om hur man arbetar med vektordata i QGIS.

3.15. Vad kommer härnäst?

I avsnittet som följer kommer vi att titta närmare på attributdata för att se hur de kan användas för att beskriva vektoregenskaper.