Viktigt

Översättning är en gemenskapsinsats du kan gå med i. Den här sidan är för närvarande översatt till 100.00%.

8. Koordinatreferenssystem

	Mål:	Förståelse av Koordinatreferenssystem.
	Nyckelord:	Koordinatreferenssystem (CRS), kartprojektion, flygprojektion, latitud, longitud, nording, östing

8.1. Översikt

Kartprojektioner försöker avbilda jordens yta, eller en del av jorden, på ett platt papper eller en datorskärm. I lekmannatermer försöker kartprojektioner omvandla jorden från dess sfäriska form (3D) till en plan form (2D).

Ett koordinatreferenssystem (CRS) definierar sedan hur den tvådimensionella, projicerade kartan i ditt GIS förhåller sig till verkliga platser på jorden. Beslutet om vilken kartprojektion och vilket CRS som ska användas beror på den regionala omfattningen av det område du vill arbeta i, på den analys du vill göra och ofta på tillgången till data.

8.2. Kartprojektion i detalj

En traditionell metod för att representera jordens form är att använda jordglober. Det finns dock ett problem med detta tillvägagångssätt. Även om jordglober bevarar merparten av jordens form och illustrerar den rumsliga konfigurationen av kontinentstora objekt, är de mycket svåra att bära med sig i fickan. De är också bara lämpliga att använda i extremt små skalor (t.ex. 1:100 miljoner).

De flesta tematiska kartdata som vanligtvis används i GIS-tillämpningar är av betydligt större skala. Typiska GIS-dataset har skalor på 1:250 000 eller större, beroende på detaljnivå. En jordglob i den här storleken skulle vara svår och dyr att producera och ännu svårare att bära med sig. Kartografer har därför utvecklat en uppsättning tekniker som kallas kartprojektioner och som är utformade för att med rimlig noggrannhet visa den sfäriska jorden i två dimensioner.

När man tittar på jorden på nära håll ser den ut att vara relativt platt. Men när vi ser den från rymden kan vi se att jorden är relativt sfärisk. Kartor, som vi kommer att se i det kommande ämnet om kartproduktion, är representationer av verkligheten. De är utformade för att inte bara representera egenskaper, utan också deras form och rumsliga arrangemang. Varje kartprojektion har fördelar och nackdelar. Vilken projektion som är bäst för en karta beror på kartans skala och på vad den ska användas till. En projektion kan t.ex. ha oacceptabla förvrängningar om den används för att kartlägga hela den afrikanska kontinenten, men kan vara ett utmärkt val för en storskalig (detaljerad) karta över ditt land. Egenskaperna hos en kartprojektion kan också påverka vissa av kartans designfunktioner. Vissa projektioner är bra för små områden, andra är bra för kartläggning av områden med en stor öst-västlig utsträckning, och andra är bättre för kartläggning av områden med en stor nord-sydlig utsträckning.

8.3. Kartprojektionernas tre familjer

Processen med att skapa kartprojektioner illustreras bäst genom att placera en ljuskälla inuti en genomskinlig jordglob på vilken ogenomskinliga jordobjekt är placerade. Därefter projiceras konturerna på ett tvådimensionellt, platt papper. Olika sätt att projicera kan åstadkommas genom att omge jordgloben på ett cylindriskt sätt, som en kon eller till och med som en platt yta. Var och en av dessa metoder ger upphov till vad som kallas en kartprojektionsfamilj. Därför finns det en familj av planar projektioner, en familj av cylindriska projektioner och en annan som kallas koniska projektioner (se Fig. 8.43)

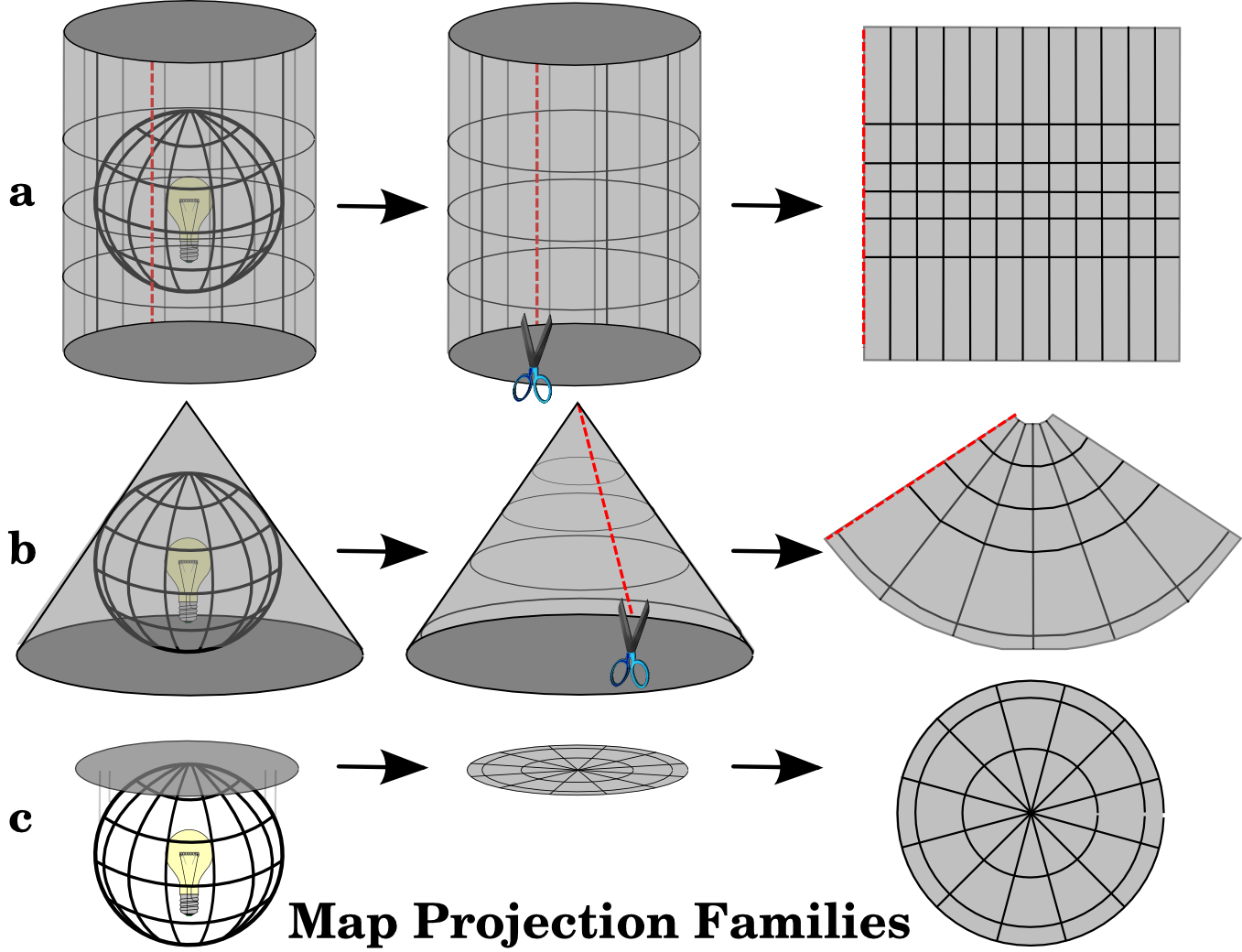
Fig. 8.43 De tre familjerna av kartprojektioner. De kan representeras av a) cylindriska projektioner, b) koniska projektioner eller c) plana projektioner.

I dag sker naturligtvis projektionen av den sfäriska jorden på ett platt papper med hjälp av de matematiska principerna geometri och trigonometri. På så sätt återskapas den fysiska projektionen av ljus genom jordgloben.

8.4. Kartprojektioners noggrannhet

Kartprojektioner är aldrig helt exakta representationer av den sfäriska jorden. Som ett resultat av kartprojektionsprocessen uppvisar varje karta förvrängningar av vinkelöverensstämmelse, avstånd och yta. En kartprojektion kan kombinera flera av dessa egenskaper eller vara en kompromiss som förvränger alla egenskaper för yta, avstånd och vinkelkonformitet inom en viss acceptabel gräns. Exempel på kompromissprojektioner är Winkel Tripel-projektionen och Robinson-projektionen (se Fig. 8.44), som ofta används för att producera och visualisera världskartor.

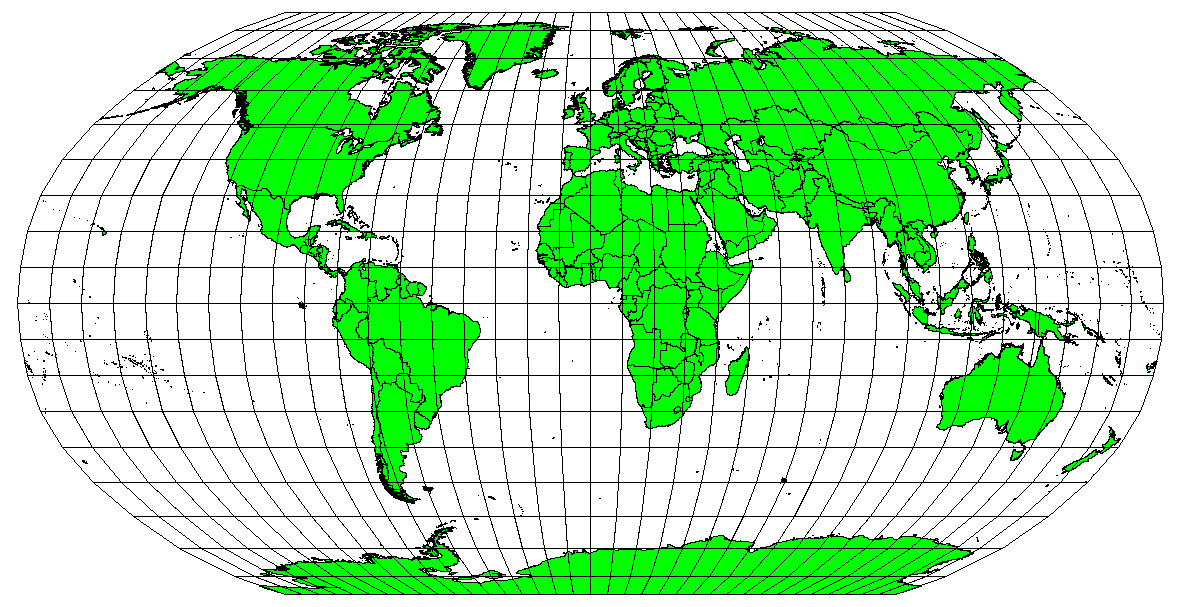
Fig. 8.44 Robinson-projektionen är en kompromiss där förvrängningar av yta, vinkelkonformitet och avstånd är acceptabla.

Det är oftast omöjligt att bevara alla egenskaper samtidigt i en kartprojektion. Det innebär att när du vill utföra noggranna analyser måste du använda en kartprojektion som ger de bästa egenskaperna för dina analyser. Om du t.ex. behöver mäta avstånd på din karta bör du försöka använda en kartprojektion för dina data som ger hög noggrannhet för avstånd.

8.4.1. Kartprojektioner med vinkelkonformitet

När man arbetar med en jordglob kommer kompassrosens huvudriktningar (norr, öster, söder och väster) alltid att befinna sig i 90 graders vinkel mot varandra. Med andra ord kommer öst alltid att befinna sig i 90 graders vinkel mot norr. Att bibehålla korrekta vinkelegenskaper kan också bevaras på en kartprojektion. En kartprojektion som bibehåller denna egenskap av vinkelkonformitet kallas en konformal eller ortomorf projektion.

Dessa projektioner används när bevarande av vinkelrelationer är viktigt. De används vanligen för navigering eller meteorologiska uppgifter. Det är viktigt att komma ihåg att det är svårt att bibehålla sanna vinklar på en karta för stora områden och att man endast bör försöka göra det för små delar av jorden. Den konforma projektionstypen resulterar i förvrängningar av områden, vilket innebär att om områdesmätningar görs på kartan kommer de att vara felaktiga. Ju större området är, desto mindre exakta blir areamätningarna. Exempel är Mercator-projektionen (som visas i Fig. 8.45) och Lambert Conformal Conic-projektionen. U.S. Geological Survey använder en konform projektion för många av sina topografiska kartor.

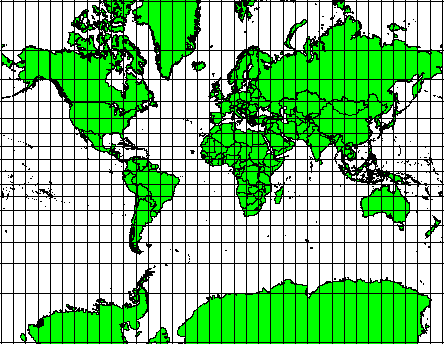
Fig. 8.45 Mercator-projektionen används t.ex. när vinkelförhållandena är viktiga, men förhållandet mellan ytor förvrängs.

8.4.2. Kartprojektioner med lika avstånd

Om ditt mål med att projicera en karta är att exakt mäta avstånd, bör du välja en projektion som är utformad för att bevara avstånd väl. Sådana projektioner, som kallas equidistanta projektioner, kräver att skalan på kartan hålls konstant. En karta är ekvidistant när den korrekt återger avstånd från projektionens mittpunkt till vilken annan plats som helst på kartan. Ekvidistanta projektioner bibehåller korrekta avstånd från projektionens mittpunkt eller längs givna linjer. Dessa projektioner används för radio- och seismisk kartläggning samt för navigering. Plate Carree Equidistant Cylindrical (se Fig. 8.46) och Equirectangular projection är två bra exempel på ekvidistanta projektioner. Den Azimuthal Equidistant-projektionen är den projektion som används för FN:s emblem (se Fig. 8.47).

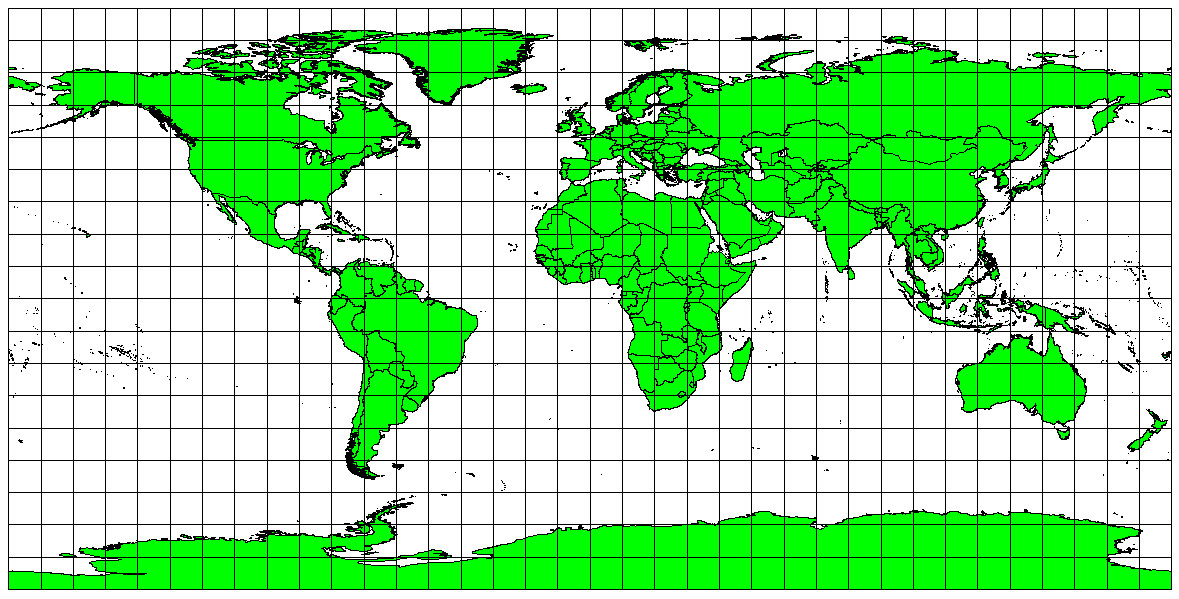
Fig. 8.46 Den cylindriska projektionen Plate Carree Equidistant används t.ex. när det är viktigt med exakt avståndsmätning.

Fig. 8.47 FN:s logotyp använder projektionen Azimuthal Equidistant.

8.4.3. Projektioner med lika stora ytor

När en karta avbildar områden över hela kartan, så att alla avbildade områden har samma proportionella förhållande till de områden på jorden som de representerar, är kartan en karta med lika områden. I praktiken kräver allmänna referens- och utbildningskartor oftast användning av projektioner med samma yta. Som namnet antyder används dessa kartor bäst när arealberäkningar är de dominerande beräkningar som du kommer att utföra. Om du t.ex. försöker analysera ett visst område i din stad för att ta reda på om det är tillräckligt stort för ett nytt köpcentrum, är projektioner med lika stor yta det bästa valet. Å ena sidan, ju större område du analyserar, desto mer exakta blir dina areamått om du använder en projektion med lika stora ytor i stället för en annan typ. Å andra sidan leder en projektion med lika stora ytor till avvikelser i vinkelöverensstämmelse när det gäller stora ytor. Små ytor löper mycket mindre risk att få sina vinklar förvrängda när du använder en projektion med lika yta. Albers likformiga projektion, Lamberts likformiga projektion och Mollweides likformiga cylindriska projektion (visas i Fig. 8.48) är typer av likformiga projektioner som ofta förekommer i GIS-arbete.

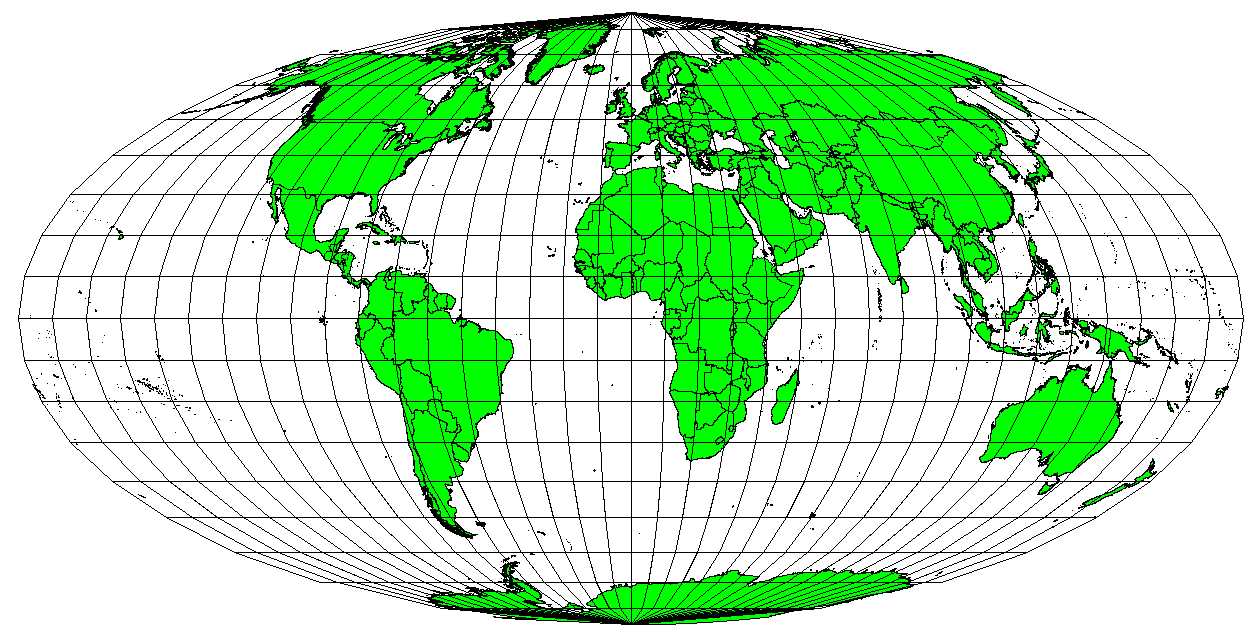
Fig. 8.48 Mollweide Equal Area Cylindrical projection säkerställer till exempel att alla kartlagda områden har samma proportionella förhållande till områdena på jorden.

Tänk på att kartprojektion är ett mycket komplext ämne. Det finns hundratals olika projektioner tillgängliga över hela världen som alla försöker avbilda en viss del av jordens yta så troget som möjligt på ett platt papper. I verkligheten kommer valet av vilken projektion du ska använda ofta att göras åt dig. De flesta länder har vanliga projektioner och när data utbyts kommer människor att följa den nationella trenden.

8.5. Koordinatreferenssystem (CRS) i detalj

Med hjälp av koordinatreferenssystem (CRS) kan varje plats på jorden anges med en uppsättning av tre tal, som kallas koordinater. Generellt kan CRS delas in i projicerade koordinatreferenssystem (även kallade kartesiska eller rektangulära koordinatreferenssystem) och geografiska koordinatreferenssystem.

8.5.1. Geografiska koordinatsystem

Geografiska koordinatsystem är mycket vanliga. De använder latitud- och longitudgrader och ibland även ett höjdvärde för att beskriva en plats på jordens yta. Det mest populära kallas WGS 84.

Latitudlinjer löper parallellt med ekvatorn och delar in jorden i 180 lika stora delar från norr till söder (eller söder till norr). Referenslinjen för latitud är ekvatorn och varje hemisfär är indelad i nittio sektioner, som var och en representerar en latitudgrad. På norra halvklotet mäts latitudgraderna från noll vid ekvatorn till nittio vid nordpolen. På södra halvklotet mäts latitudgraderna från noll vid ekvatorn till nittio grader vid sydpolen. För att förenkla digitaliseringen av kartor tilldelas latitudgraderna på södra halvklotet ofta negativa värden (0 till -90°). Var du än befinner dig på jordytan är avståndet mellan latitudlinjerna detsamma (60 nautiska mil). Se Fig. 8.49 för en bildmässig vy.

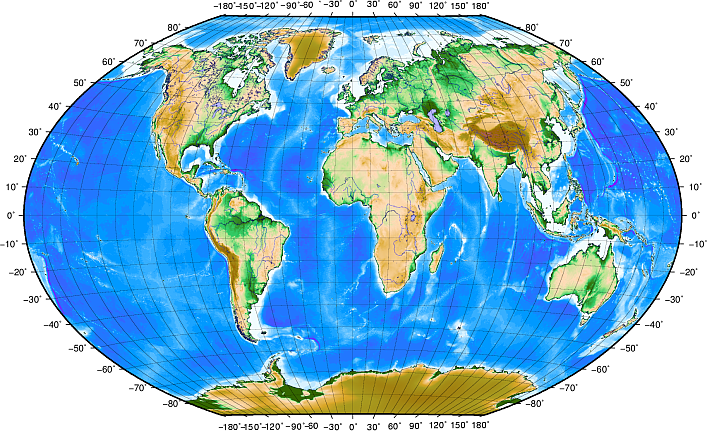
Fig. 8.49 Geografiskt koordinatsystem med latitudlinjer parallella med ekvatorn och longitudlinjer med nollmeridianen genom Greenwich.

Longitudlinjer, å andra sidan, står sig inte så bra mot standarden för enhetlighet. Longitudlinjerna går vinkelrätt mot ekvatorn och konvergerar vid polerna. Referenslinjen för longitud (nollmeridianen) går från nordpolen till sydpolen genom Greenwich i England. Efterföljande longitudlinjer mäts från noll till 180 grader öster eller väster om nollmeridianen. Observera att värden väster om nollmeridianen tilldelas negativa värden för användning i digitala kartapplikationer. Se Fig. 8.49 för en bildmässig vy.

Vid ekvatorn, och endast vid ekvatorn, är avståndet som representeras av en longitudlinje lika med avståndet som representeras av en latitudgrad. När du rör dig mot polerna blir avståndet mellan longitudlinjerna gradvis mindre, tills alla 360° longitud vid polens exakta läge representeras av en enda punkt som du kan sätta fingret på (du skulle förmodligen vilja bära handskar dock). Med hjälp av det geografiska koordinatsystemet har vi ett rutnät av linjer som delar in jorden i kvadrater som täcker cirka 12363,365 kvadratkilometer vid ekvatorn — en bra början, men inte särskilt användbar för att bestämma platsen för något inom den kvadraten.

För att vara riktigt användbart måste ett kartnät delas in i tillräckligt små delar så att de kan användas för att beskriva (med en acceptabel noggrannhet) var en punkt på kartan befinner sig. För att åstadkomma detta delas graderna in i minuter (') och sekunder ("). Det går sextio minuter på en grad och sextio sekunder på en minut (3600 sekunder på en grad). Så vid ekvatorn är en sekunds latitud eller longitud = 30,87624 meter.

8.5.2. Projicerat koordinatsystem

Ett tvådimensionellt koordinatreferenssystem definieras vanligen av två axlar. I rät vinkel mot varandra bildar de ett så kallat XY-plan (se Fig. 8.50 på vänster sida). Den horisontella axeln betecknas normalt X och den vertikala axeln betecknas normalt Y. I ett tredimensionellt koordinatreferenssystem läggs ytterligare en axel till, normalt märkt Z. Den ligger också i rät vinkel mot axlarna X och Y. Axeln Z ger den tredje dimensionen av rymden (se Fig. 8.50 på höger sida). Varje punkt som uttrycks i sfäriska koordinater kan uttryckas som en X Y Z-koordinat.

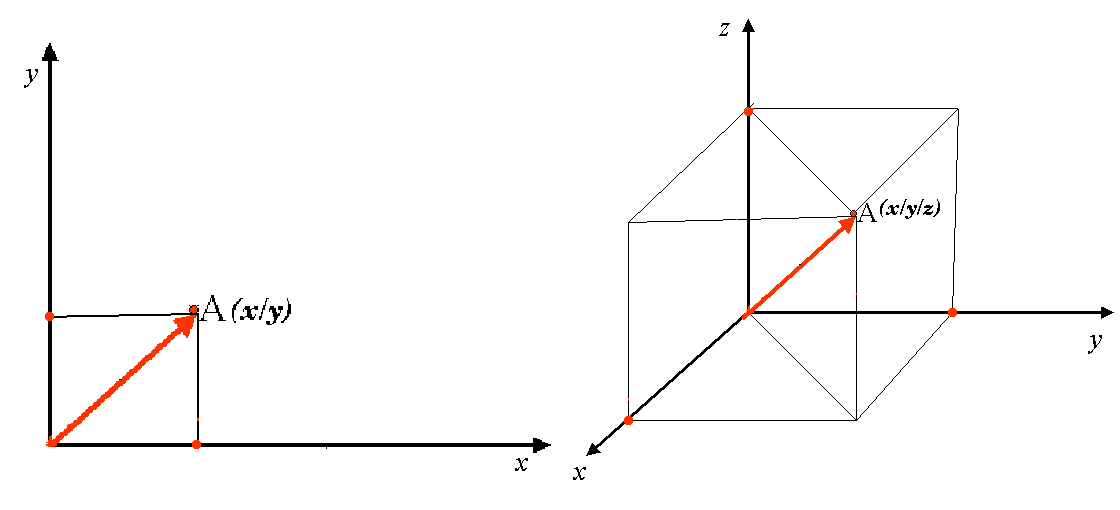
Fig. 8.50 Två- och tredimensionella koordinatreferenssystem.

Ett projicerat koordinatreferenssystem på södra halvklotet (söder om ekvatorn) har normalt sitt ursprung på ekvatorn vid en viss Longitud. Detta innebär att Y-värdena ökar söderut och X-värdena ökar västerut. På norra halvklotet (norr om ekvatorn) är ursprunget också ekvatorn på en viss longitud. Nu ökar dock Y-värdena norrut och X-värdena ökar österut. I följande avsnitt beskriver vi ett projicerat koordinatreferenssystem, kallat Universal Transverse Mercator (UTM), som ofta används för Sydafrika.

8.6. Universal Transverse Mercator (UTM) CRS i detalj

Referenssystemet UTM (Universal Transverse Mercator) har sitt ursprung på ekvatorn vid en viss longitud. Nu ökar Y-värdena söderut och X-värdena ökar västerut. UTM CRS är en global kartprojektion. Det innebär att den i allmänhet används över hela världen. Men som redan beskrivits i avsnittet ”Kartprojektionernas noggrannhet” ovan, desto större område (t.ex. Sydafrika) desto mer snedvridning av vinkelkonformitet, avstånd och område uppstår. För att undvika alltför stora förvrängningar delas världen in i 60 lika stora zoner som alla är 6 grader breda i longitud från öst till väst. UTM-zonerna är numrerade 1 till 60, med början vid antimeridianen (zon 1 på 180 graders västlig longitud) och fortsätter österut tillbaka till antemeridianen (zon 60 på 180 graders östlig longitud) enligt Fig. 8.51.

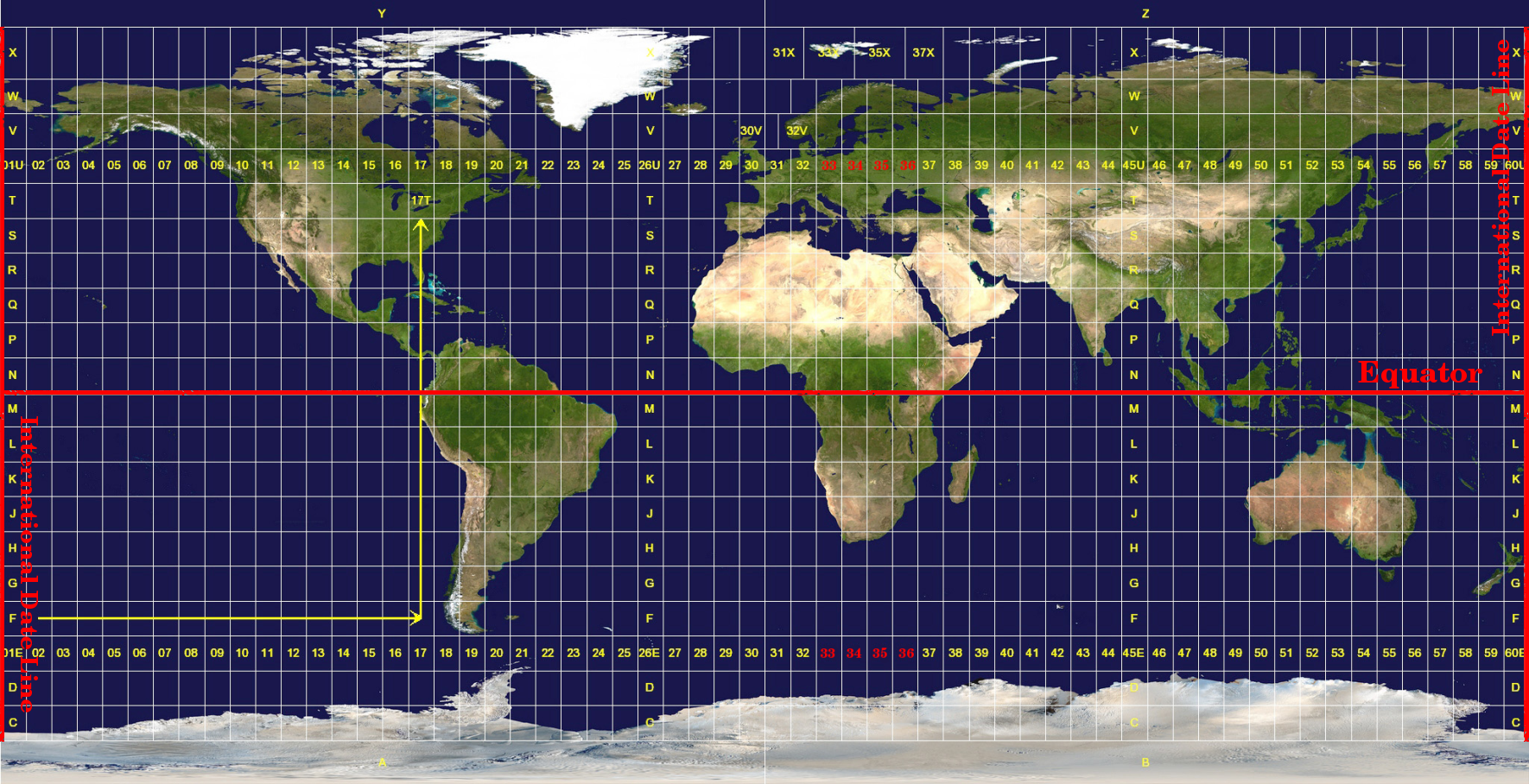
Fig. 8.51 De universella tvärgående Mercator-zonerna. För Sydafrika används UTM-zonerna 33S, 34S, 35S och 36S.

Som du kan se i Fig. 8.51 och Fig. 8.52 täcks Sydafrika av fyra UTM-zoner för att minimera distorsionen. Zonerna kallas UTM 33S, UTM 34S, UTM 35S och UTM 36S. S efter zonen betyder att UTM-zonerna är belägna syd om ekvatorn.

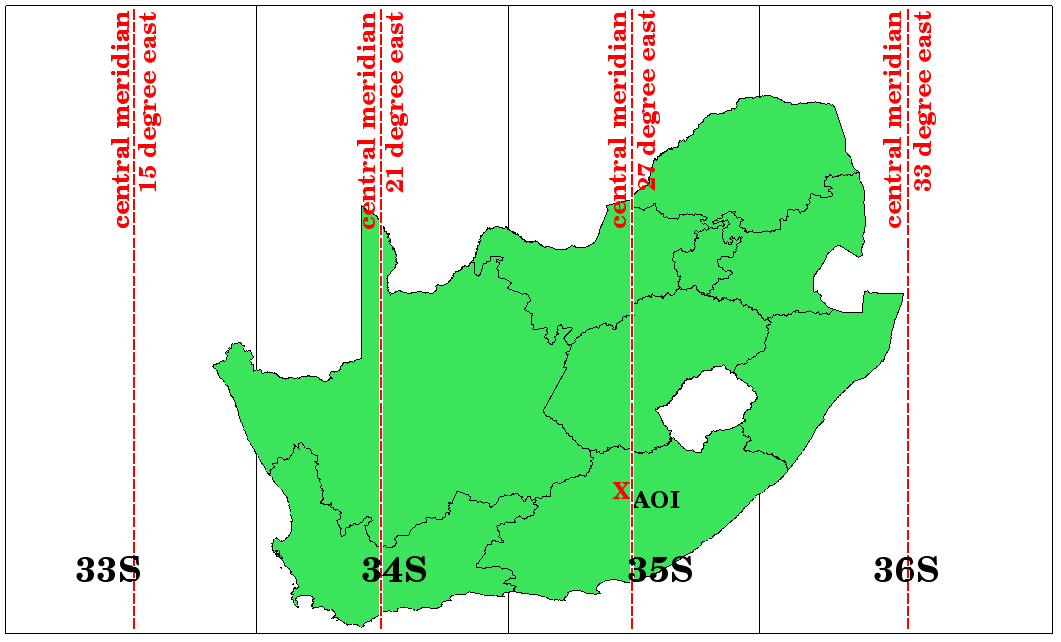
Fig. 8.52 UTM-zonerna 33S, 34S, 35S och 36S med sina centrala longituder (meridianer) som används för att projicera Sydafrika med hög noggrannhet. Det röda korset visar ett intresseområde (AOI).

Säg till exempel att vi vill definiera en tvådimensionell koordinat inom Area of Interest (AOI) markerad med ett rött kors i Fig. 8.52. Du kan se, att området ligger inom UTM-zonen 35S. Detta innebär att vi bör använda UTM-zon 35S som koordinatreferenssystem för att minimera distorsion och få korrekta analysresultat.

Positionen för en koordinat i UTM söder om ekvatorn måste anges med zonens nummer (35) och med dess nordostvärde (Y) och östvärde (X) i meter. Värdet för nordlig riktning är positionens avstånd från ekvatorn i meter. Värdet easting är avståndet från centralmeridianen (longitud) i den UTM-zon som används. För UTM-zon 35S är det 27 grader East, vilket visas i Fig. 8.52. Eftersom vi befinner oss söder om ekvatorn och negativa värden inte är tillåtna i UTM-koordinatreferenssystemet måste vi dessutom lägga till ett så kallat falskt nordvärde på 10 000 000 m till nordvärdet (Y) och ett falskt östvärde på 500 000 m till östvärdet (X). Det här låter svårt, så vi ska göra ett exempel som visar hur du hittar rätt UTM 35S-koordinat för intresseområdet.

8.6.1. Värdet för nordlig riktning (Y)

Platsen vi letar efter ligger 3 550 000 meter söder om ekvatorn, så nordvärdet (Y) får ett negativt tecken och är -3 550 000 m. Enligt UTM-definitionerna måste vi lägga till ett falskt nordvärde på 10 000 000 m. Detta innebär att nordvärdet (Y) för vår koordinat är 6 450 000 m (-3 550 000 m + 10 000 000 m).

8.6.2. Värde för ostlig riktning (X)

Först måste vi hitta den centrala meridianen (longitud) för UTM-zonen 35S. Som vi kan se i Fig. 8.52 är den 27 grader öst. Den plats vi letar efter ligger 85 000 meter västerut från centralmeridianen. Precis som värdet för nordlig riktning får värdet för östlig riktning (X) ett negativt tecken, vilket ger resultatet -85 000 m. Enligt UTM-definitionerna måste vi lägga till ett falskt östvärde på 500 000 m. Detta innebär att östvärdet (X) för vår koordinat är 415 000 m (-85 000 m + 500 000 m). Slutligen måste vi lägga till zonens nummer till easting-värdet för att få rätt värde.

Som ett resultat skulle koordinaten för vår intressepunkt, projicerad i UTM-zon 35S skrivas som: 35 415,000 m E / 6 450,000 m N. I vissa GIS, när rätt UTM-zon 35S har definierats och enheterna är inställda på meter i systemet, kan koordinaten också helt enkelt visas som 415 000 6 450 000.

8.7. On-the-Fly-projektion

Som du säkert kan föreställa dig kan det uppstå situationer där de data som du vill använda i ett GIS projiceras i olika koordinatreferenssystem. Du kan t.ex. få ett vektorlager som visar Sydafrikas gränser projicerade i UTM 35S och ett annat vektorlager med punktinformation om nederbörd i det geografiska koordinatsystemet WGS 84. I GIS placeras dessa två vektorlager i helt olika delar av kartfönstret, eftersom de har olika projektioner.

För att lösa detta problem innehåller många GIS en funktion som kallas on-the-fly-projektion. Det innebär att du kan definiera en viss projektion när du startar GIS och alla lager som du sedan laddar, oavsett vilket koordinatreferenssystem de har, kommer automatiskt att visas i den projektion som du definierade. Med den här funktionen kan du lägga lager över varandra i kartfönstret i ditt GIS, även om de har olika referenssystem. I QGIS används den här funktionen som standard.

8.8. Vanliga problem / saker att vara uppmärksam på

Ämnet kartprojektion är mycket komplext och även yrkesverksamma som har studerat geografi, geodetik eller någon annan GIS-relaterad vetenskap har ofta problem med den korrekta definitionen av kartprojektioner och koordinatreferenssystem. När du arbetar med GIS har du vanligtvis redan projicerade data att utgå ifrån. I de flesta fall kommer dessa data att projiceras i ett visst CRS, så att du inte behöver skapa ett nytt CRS eller ens omprojicera data från ett CRS till ett annat. Med det sagt är det alltid bra att ha en uppfattning om vad kartprojektion och CRS innebär.

8.9. Vad har vi lärt oss?

Låt oss sammanfatta vad vi behandlat i det här arbetsbladet:

• Kartprojektioner avbildar jordens yta på ett tvådimensionellt, platt papper eller en datorskärm.

• Det finns globala kartprojektioner, men de flesta kartprojektioner är skapade och optimerade för att projicera mindre områden av jordens yta.

• Kartprojektioner är aldrig helt exakta avbildningar av den sfäriska jorden. De uppvisar avvikelser i vinkelöverensstämmelse, avstånd och yta. Det är omöjligt att bevara alla dessa egenskaper samtidigt i en kartprojektion.

• Ett Coordinate reference system (CRS) definierar, med hjälp av koordinater, hur den tvådimensionella, projicerade kartan är relaterad till verkliga platser på jorden.

• Det finns två olika typer av koordinatreferenssystem: Geografiska koordinatsystem och Projicerade koordinatsystem.

• On the Fly-projektion är en funktion i GIS som gör att vi kan överlagra lager, även om de projiceras i olika koordinatreferenssystem.

8.10. Nu får du försöka!

Här är några idéer som du kan prova med dina elever:

1. Starta QGIS

2. I Projekt ► Egenskaper… ► CRS kontrollera Ingen projektion (eller okänd/ej jordprojektion)

3. Ladda två lager av samma yta men med olika projektioner

4. Låt dina elever hitta koordinaterna för flera platser på de två lagren. Du kan visa dem att det inte går att lägga de två lagren över varandra.

5. Definiera sedan referenssystemet för koordinaterna som Geographic/WGS 84 i dialogrutan Project Properties

6. Ladda de två lagren av samma område igen och låt eleverna se hur det fungerar att ställa in ett CRS för projektet (och därmed möjliggöra projicering ”on-the-fly”).

7. Du kan öppna dialogrutan Project Properties i QGIS och visa dina elever de många olika koordinatreferenssystemen så att de får en uppfattning om hur komplext det här ämnet är. Du kan välja olika CRS för att visa samma skikt i olika projektioner.

8.11. Något att tänka på

Om du inte har tillgång till en dator kan du visa dina elever principerna för de tre kartprojektionsfamiljerna. Ta fram en jordglob och ett papper och visa hur cylindriska, koniska och plana projektioner fungerar i allmänhet. Med hjälp av ett genomskinligt ark kan du rita ett tvådimensionellt koordinatreferenssystem som visar X-axlar och Y-axlar. Låt sedan eleverna definiera koordinater (X- och Y-värden) för olika platser.

8.12. Ytterligare läsning

Böcker:

• Chang, Kang-Tsung (2006). Introduktion till geografiska informationssystem. 3:e upplagan. McGraw Hill. ISBN: 0070658986

• DeMers, Michael N. (2005). Grunderna i geografiska informationssystem. 3:e upplagan. Wiley. ISBN: 9814126195

• Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X

Webbplatser:

• https://foote.geography.uconn.edu/gcraft/notes/mapproj/mapproj_f.html

• http://geology.isu.edu/wapi/geostac/Field_Exercise/topomaps/index.htm

QGIS User Guide innehåller också mer detaljerad information om hur du arbetar med kartprojektioner i QGIS.

8.13. Vad kommer härnäst?

I avsnittet som följer kommer vi att titta närmare på Map Production.