3. Vektorová data
Cíle: |
Pochopení vektorových datových modelů užitím v GIS. |
|
Klíčová slova: |
Vektor, Bod, Křivka, Polygon, Vrchol, Geometrie, Měřítko, Kvalita Dat, Symbologie, Zdroje Dat |
3.1. Přehled
Vector data provide a way to represent real world features within the GIS environment. A feature is anything you can see on the landscape. Imagine you are standing on the top of a hill. Looking down you can see houses, roads, trees, rivers, and so on (see Obr. 3.28). Each one of these things would be a feature when we represent them in a GIS Application. Vector features have attributes, which consist of text or numerical information that describe the features.

Obr. 3.28 Při pohledu na krajinou můžete vidět hlavní rysy, jako jsou silnice, domy a stromy.
A vector feature has its shape represented using geometry. The geometry is
made up of one or more interconnected vertices. A vertex describes a position
in space using an X, Y and optionally Z axis. Geometries which have
vertices with a Z axis are often referred to as 2.5D since they describe
height or depth at each vertex, but not both.
When a feature’s geometry consists of only a single vertex, it is referred to as a point feature (see illustration Obr. 3.29). Where the geometry consists of two or more vertices and the first and last vertex are not equal, a polyline feature is formed (see illustration Obr. 3.30). Where three or more vertices are present, and the last vertex is equal to the first, an enclosed polygon feature is formed (see illustration Obr. 3.31).
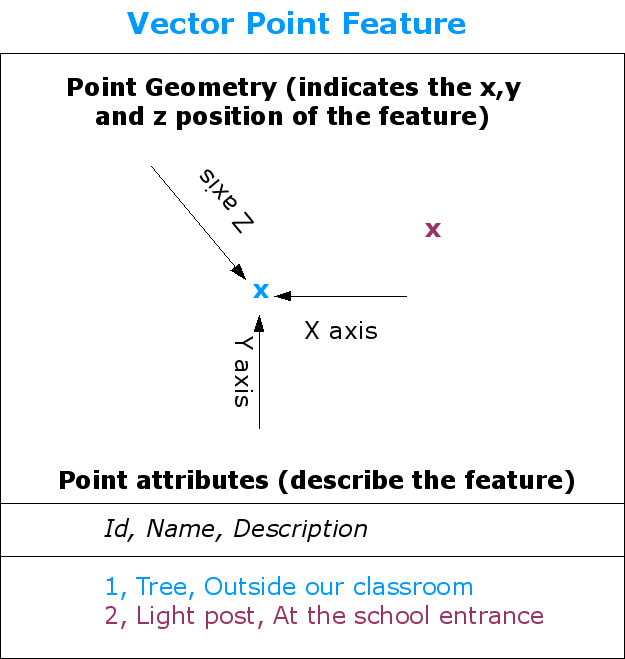
Obr. 3.29 Bodová funkce je popsána jeho X, Y a případně Z souřadnicí. Bodové atributy popisují bod např. zda se jedná o strom nebo sloup veřejného osvětlení.
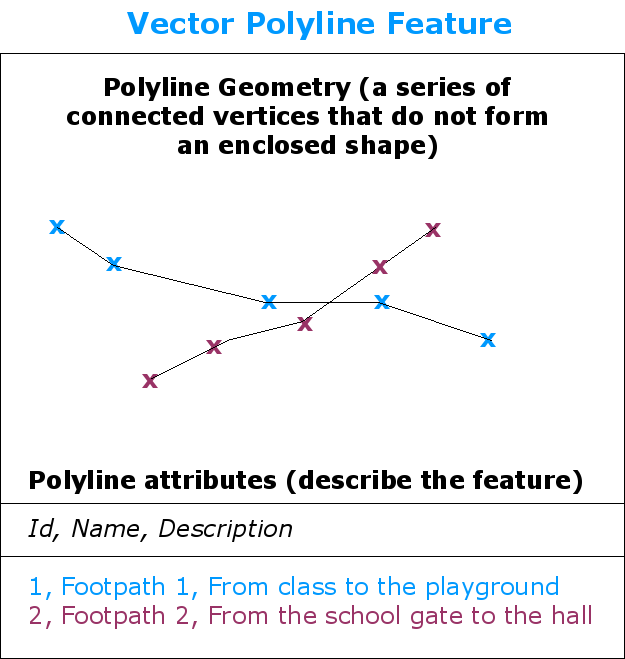
Obr. 3.30 Křivka je sekvence spojených vrcholů. Každý vrchol má X, Y (a volitelně Z) souřadnici. Atributy popisují danou křivku.
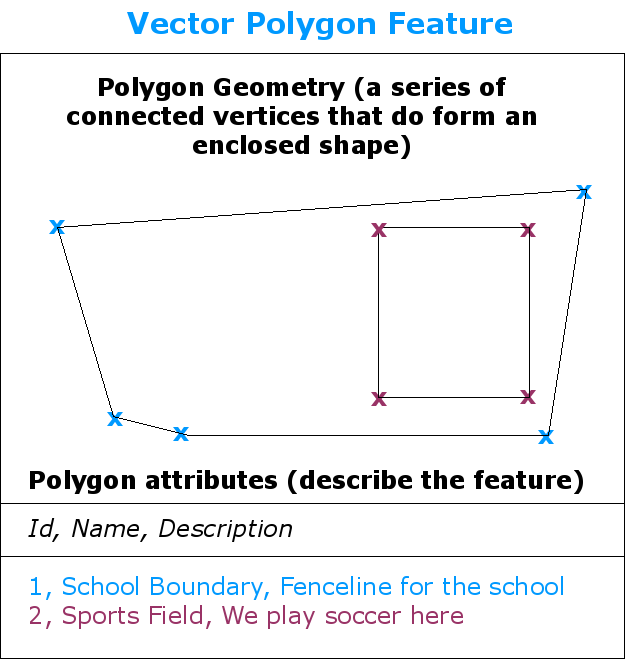
Obr. 3.31 Polygon stejně jako křivka, je sekvence vrcholů. Avšak v polygonu, první a poslední vrcholy jsou vždy na stejném místě.
Looking back at the picture of a landscape we showed you further up, you should be able to see the different types of features in the way that a GIS represents them now (see illustration Obr. 3.32).
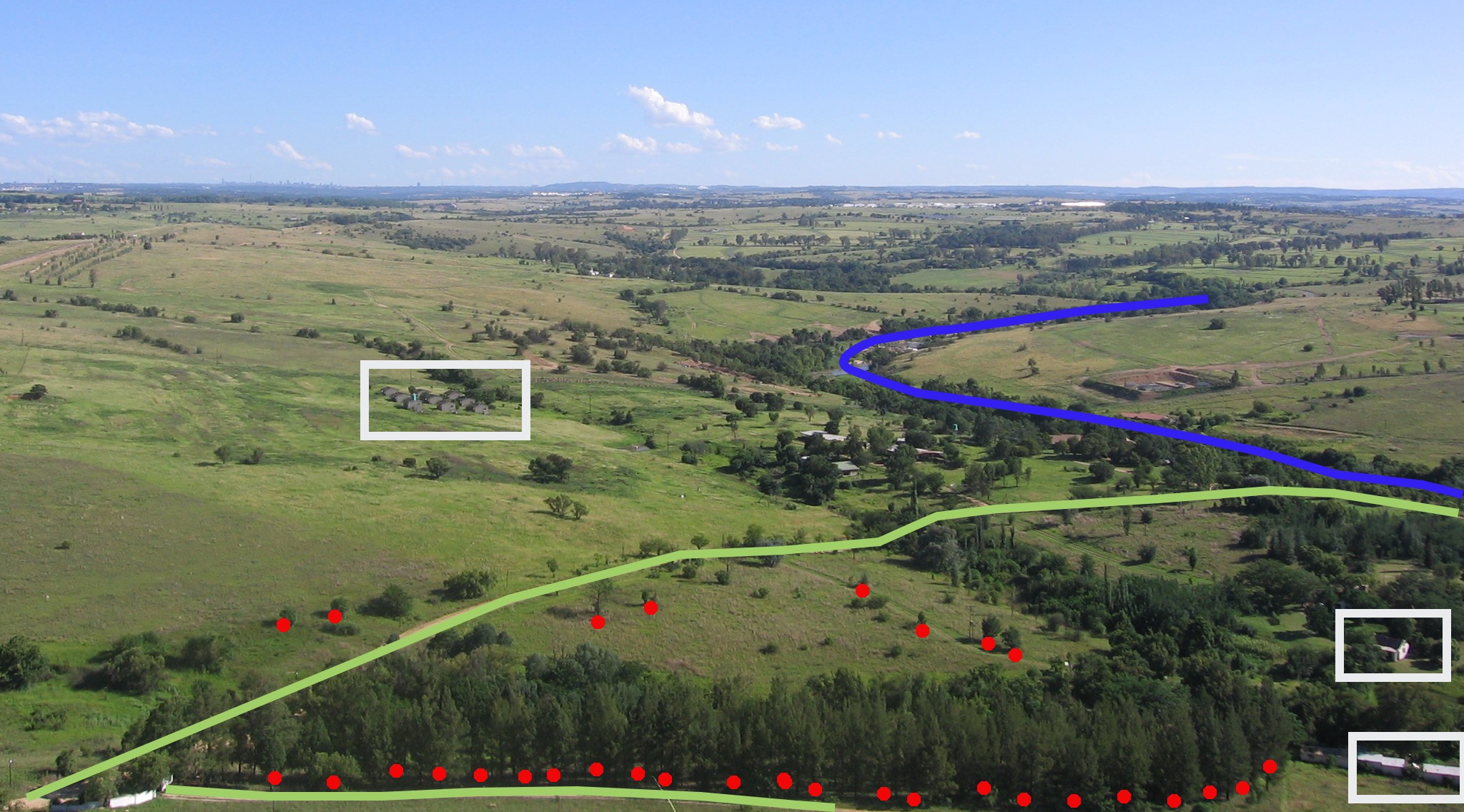
Obr. 3.32 Krajinné funkce, jak bychom je prezentovali v GIS. Řeky (modré) a silnice (zelené) mohou být reprezentovány jako čáry, stromy jako body (červeně) a domy jako polygony (bílou).
3.2. Bodové funkce v detailu.
První věc, kterou si musíme uvědomit, když mluví o bodových funkcí je, že to, co popisujeme jako bod v GIS je věc názoru, a často je to závislé na měřítku. Podívejme se například na města. Pokud máte malé měřítko mapy (což pokrývá rozsáhlou oblast), může mít smysl reprezentovat město pomocí funkce bodu. Nicméně, když sepřiblížíte na mapu, pohybující se směrem k větším měřítku, dává větší smysl ukazovat hranice města pomocí polygonu.
Když se rozhodnete použít body představující rys je většinou otázkou měřítka (jak daleko jste od funkce), pohodlí (trvá méně času a úsilí o vytvoření bodových funkcí než polygonu funkcí) a typ prvku (některé věci, jako telegrafní sloupy prostě nemají smysl být uloženy jako polygony).
As we show in illustration Obr. 3.29, a point feature has an X, Y and optionally, Z value. The X and Y values will depend on the Coordinate Reference System (CRS) being used. We are going to go into more detail about Coordinate Reference Systems in a later tutorial. For now let’s simply say that a CRS is a way to accurately describe where a particular place is on the earth’s surface. One of the most common reference systems is Longitude and Latitude. Lines of Longitude run from the North Pole to the South Pole. Lines of Latitude run from the East to West. You can describe precisely where you are at any place on the earth by giving someone your Longitude (X) and Latitude (Y). If you make a similar measurement for a tree or a telephone pole and marked it on a map, you will have created a point feature.
Protože víme, že Země není plochá, je často užitečné přidat hodnotu Z do funkce bodu. Tato hodnota popisuje, jak vysoko nad mořem jste.
3.3. Funkce křivky v detailu
Where a point feature is a single vertex, a polyline has two or more vertices. The polyline is a continuous path drawn through each vertex, as shown in Obr. 3.30. When two vertices are joined, a line is created. When more than two are joined, they form a ‚line of lines‘, or polyline.
Křivka se používá k zobrazení geometrie „lineárních rysů“, jako jsou silnice, řeky, obrysů, chodníků, drah letu a tak dále. Někdy máme zvláštní pravidla pro křivky kromě jejich základní geometrie. Například vrstevnice se může dotknout (např. na útesu), ale nikdy by neměly překračovat přes sebe. Podobně křivky sloužící k ukládání silničních síťi by měly být přopojeny na křižovatkách. V některých GIS aplikacích můžete nastavit tyto zvláštní pravidla pro typ prvku (například komunikace) a GIS zajistí, aby tyto křivky vždy souhlasily v souladu s těmito pravidly.
If a curved polyline has very large distances between vertices, it may appear angular or jagged, depending on the scale at which it is viewed (see Obr. 3.33). Because of this it is important that polylines are digitised (captured into the computer) with distances between vertices that are small enough for the scale at which you want to use the data.
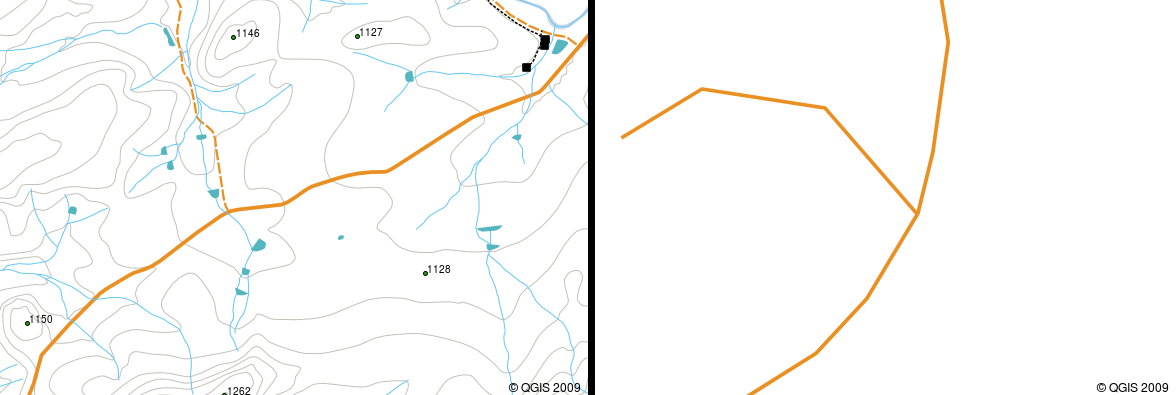
Obr. 3.33 Křivky zobrazené v menším měřítku (1:20 000 a větším) se může objevit hladce a zakřiveně. Při přiblížení k větším měřítku (1: 500) křivky můžou vypadat velmi hranatě.
The attributes of a polyline describe its properties or characteristics. For example a road polyline may have attributes that describe whether it is surfaced with gravel or tar, how many lanes it has, whether it is a one way street, and so on. The GIS can use these attributes to symbolise the polyline feature with a suitable colour or line style.
3.4. Funkce polygonu v detailu
Funkce polygonu jsou „uzavřené prostory“ jako přehrady, ostrovy, hranice zemí a tak dále. Jako lomenné funkce, jsou polygony vytvořeny z řady vrcholů, které jsou spojeny kontinuální linií. Nicméně, protože mnohoúhelník popisuje vždy uzavřenou oblast, první a poslední vrchol by měl být vždy na stejném místě! Polygony mají často „sdílenou geometrii“ — hranice, které jsou společné se sousedním polygonem. Mnoho aplikací GIS mají schopnost zajistit, že hranice sousedních polygonů se mají přesně shodovat. Toto budeme zkoumat v: ref:gentle_gis_topology téma později v tomto výukovém programu.
Stejně jako u bodů a křivek, polygony mají „atributy“. Tyto atributy popisují každý polygon. Například přehrada může mít atributy pro hloubku a kvalitu vody.
3.5. Vektorová data ve vrstvách
Now that we have described what vector data is, let’s look at how vector data is managed and used in a GIS environment. Most GIS applications group vector features into layers. Features in a layer have the same geometry type (e.g. they will all be points) and the same kinds of attributes (e.g. information about what species a tree is for a trees layer). For example if you have recorded the positions of all the footpaths in your school, they will usually be stored together on the computer hard disk and shown in the GIS as a single layer. This is convenient because it allows you to hide or show all of the features for that layer in your GIS application with a single mouse click.
3.6. Editování vektorových dat
Aplikace GIS vám umožní vytvářet a upravovat data geometrie ve vrstvě - proces se nazývá „digitalizace“ - kterým se budeme zabývat podrobněji v pozdějším tutoriálu. Jestliže obsahuje vrstva polygony (například zemědělské přehrady), aplikace GIS pouze umožňují vytvořit nové polygony v této vrstvě. Stejně tak, pokud chcete změnit tvar prvku, aplikace povolí pouze vám, jak to udělat, za předpokladu, že je změněný tvar správný. Například to nedovolí upravovat čáru takovým způsobem, že to má jen jeden vrchol - pamatujte si z dřívější diskuze o liniích, že všechny linii musí mít alespoň dva vrcholy.
Vytváření a úprava vektorových dat je důležitou funkcí GIS, protože je jednou z hlavních způsobů, kterými si můžete vytvořit osobní údaje pro věci, které nás zajímají. Řekněme například, že sledujete znečištění v řece. Dalo by se použít GIS k digitalizaci všech výpustí přívalových vod kanalizace (jako bodových objektů). Dalo by se také digitalizovat řeku samotnou (jako rys křivky). Nakonec byste mohli provádět měření hladin pH podél toku řeky a digitalizovat místa, kde jste provedli tyto hodnoty (jako bodovou vrstva).
Stejně jako vytváření vlastních dat, je zde spousta volně dostupných vektorových dat, které můžete získat a použít. Například můžete získat vektorová data, která se zobrazí na 1:50 000 mapových listů z ředitelství Chief: Průzkumy a mapování.
3.7. Měřítko a vektorová data
Map scale is an important issue to consider when working with vector data in a GIS. When data is captured, it is usually digitised from existing maps, or by taking information from surveyor records and global positioning system devices. Maps have different scales, so if you import vector data from a map into a GIS environment (for example by digitising paper maps), the digital vector data will have the same scale issues as the original map. This effect can be seen in illustrations Obr. 3.34 and Obr. 3.35. Many issues can arise from making a poor choice of map scale. For example using the vector data in illustration Obr. 3.34 to plan a wetland conservation area could result in important parts of the wetland being left out of the reserve! On the other hand if you are trying to create a regional map, using data captured at 1:1000 000 might be just fine and will save you a lot of time and effort capturing the data.
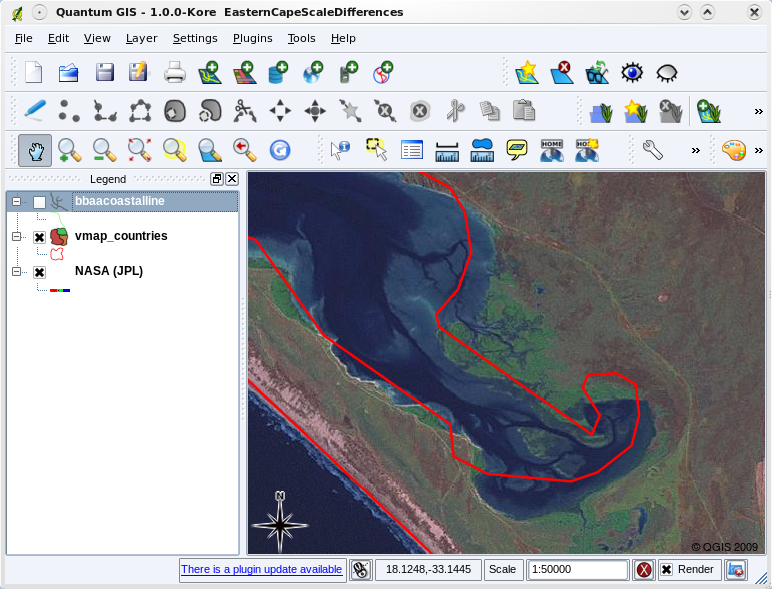
Obr. 3.34 Vektorová data (červené linie), které byly digitalizovány z maelého měřítka (1:1000 000) map.
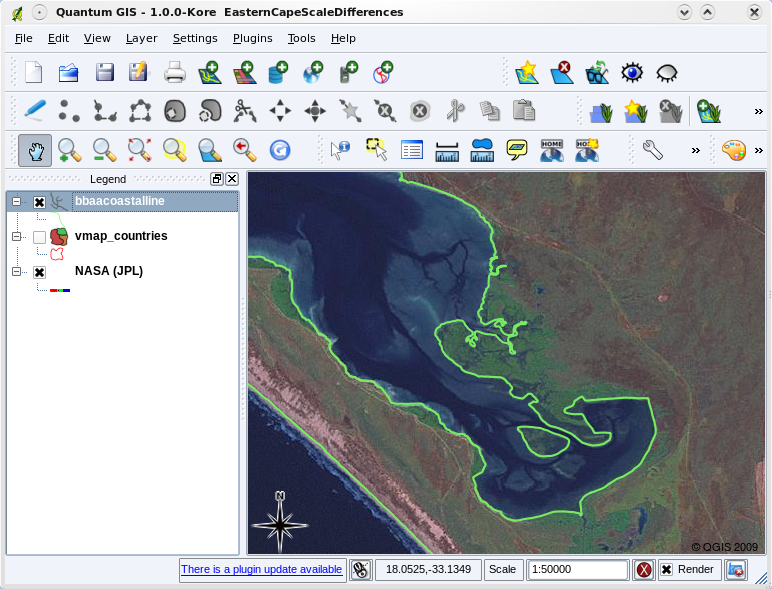
Obr. 3.35 Vektorová data (zelené linie), které byly digitalizovány z map velkých měřítek (1:50 000).
3.8. Symbologie
When you add vector layers to the map view in a GIS application, they will be drawn with random colours and basic symbols. One of the great advantages of using a GIS is that you can create personalised maps very easily. The GIS program will let you choose colours to suite the feature type (e.g. you can tell it to draw a water bodies vector layer in blue). The GIS will also let you adjust the symbol used. So if you have a trees point layer, you can show each tree position with a small picture of a tree, rather than the basic circle marker that the GIS uses when you first load the layer (see illustrations Obr. 3.36, Obr. 3.37 and Obr. 3.38).
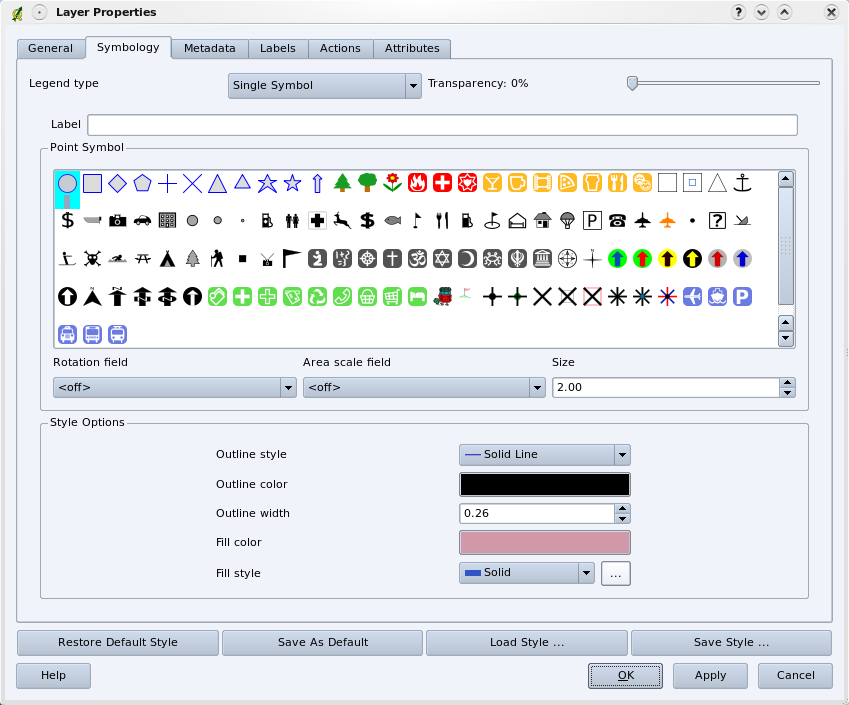
Obr. 3.36 V aplikacách GIS můžete použít panel (v liště nahoře) k nastavení, jak by se měly jednotlivé vrstvy vykreslovat.
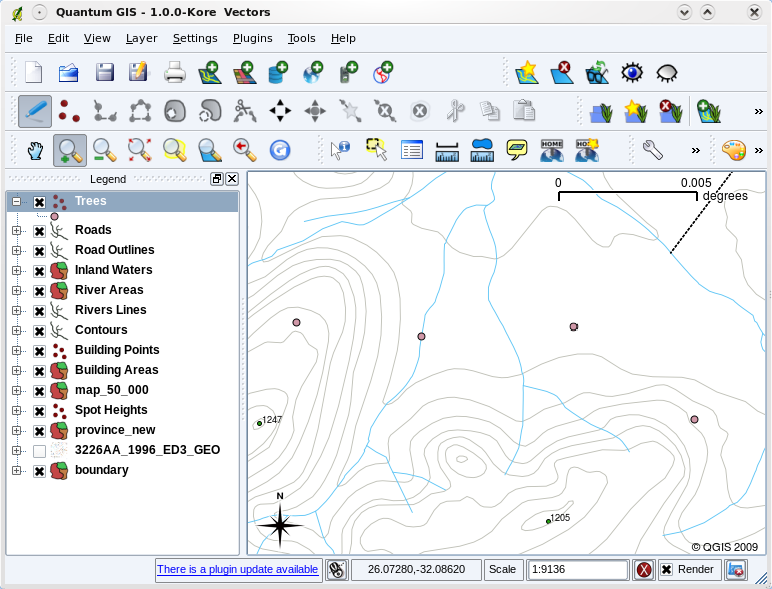
Obr. 3.37 Pokud je vrstva (například vrstva stromů nejvýšše) je první načítána, aplikace GIS jí dávají automatický symbol.
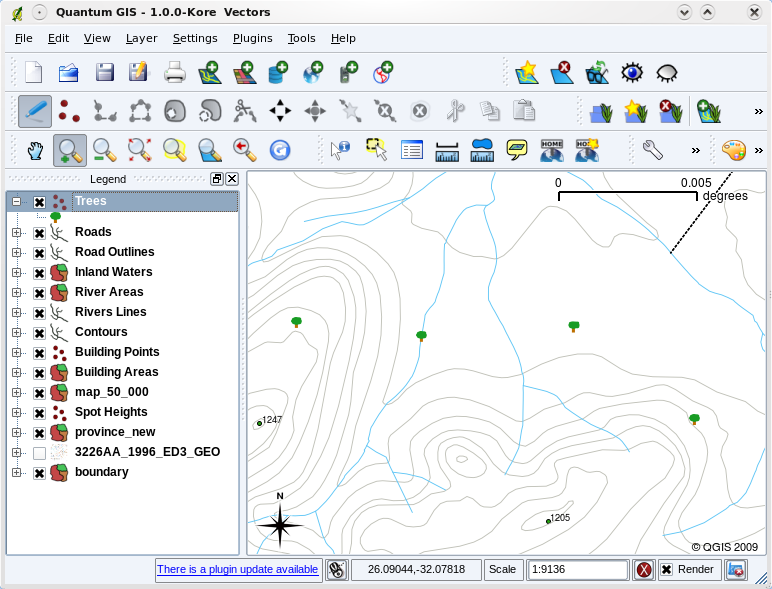
Obr. 3.38 Po provedení našeho nastavení je mnohem jednodušší vidět že naše body reprezentují stromy.
Symbolika je silný nástroj, pomocí něhož mapy ožívají a data jsou v aplikacích GIS srozumitelnější. V tématu, který následuje (ref:: gentle_gis_attributes) budeme zkoumat hlouběji, jak může symbolika pomoci uživateli pochopit vektorová data.
3.9. Co můžeme dělat s vektorovými daty v aplikacích GIS?
Na nejjednodušší úrovni můžeme použít vektorová data v GIS aplikacích v podstatě stejným způsobem, jako byste použili normální topografické mapy. Skutečná síla GIS začíná, když začnete klást otázky, „Které domy jsou v rámci 100 let úrovně povodňové řeky?“; „Kde je nejlepší místo pro nemocnice tak, že je snadno přístupný co největšímu počtu lidí je možné? ‚; „Který studující žijí v určitém předměstí?“. GIS je skvělý nástroj pro odpovědi na tyto typy otázek pomocí vektorových dat. Obecně máme na mysli proces odpovědi na tyto typy otázek jako „prostorové analýzy“. V pozdějších tématech tohoto tutoriálu se podíváme na prostorové analýzy podrobněji.
3.10. Obvyklé problémy s vektorovými daty
Práce s vektorovými daty má určitá úskalí. Již jsme zmínili problémy, které mohou nastat s vektory zachycených v různých měřítcích. Vektorová data také potřebují hodně práce a údržby, aby bylo zajištěno, že jsou přesné a spolehlivé. Nepřesné vektorová data mohou nastat, když nástroje použité k zachycení dat nejsou správně nastaveny, když lidé zachycující data nejsou příliš opatrní, když čas nebo peníze neumožňují dostatečně podrobný sběr dat a tak dále.
If you have poor quality vector data, you can often detect this when viewing the data in a GIS. For example slivers can occur when the edges of two polygon areas don’t meet properly (see Obr. 3.39).
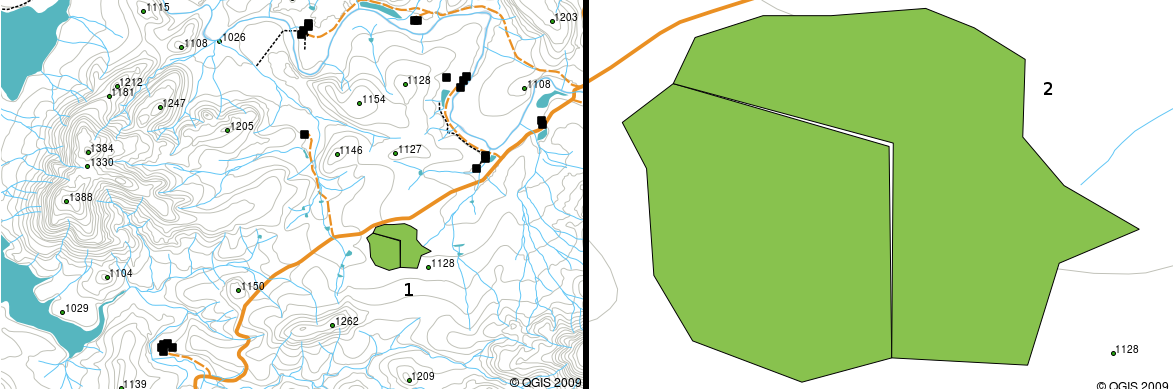
Obr. 3.39 Nedokonalosti mohou nastat, když vrcholy dvou polygonů neodpovídají na jejich hranicích. V malých měřítkách (1 zleva) nemusíte být schopni vidět tyto chyby. Ve velkém měřítku jsou viditelné jako tenké proužky mezi dvěma polygony (2 zprava).
Overshoots can occur when a line feature such as a road does not meet another road exactly at an intersection. Undershoots can occur when a line feature (e.g. a river) does not exactly meet another feature to which it should be connected. Figure Obr. 3.40 demonstrates what undershoots and overshoots look like.
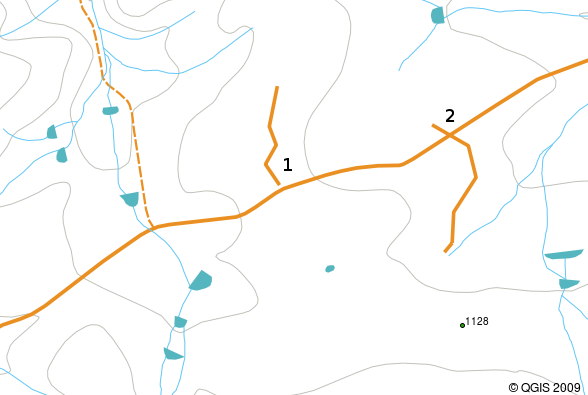
Obr. 3.40 Nedotahy (1) nastávají, když digitalizované vektorové linie, které by se měly připojit k sobě nemají zcela přesný dotek. Překmity (2) se stávají, když linie končí za hranicí, kde by se měla připojit.
Vzhledem k typům těchto chyb, je velmi důležité, aby byla data pečlivě a přesně digitalizovat. V nadcházejícím tématu na „topologii“, budeme zkoumat některé z těchto typů chyb podrobněji.
3.11. Co už jsme se naučili?
Pojďme si shrnout, co jsme se naučili v tomto prostředí.
„Vektorová data“ jsou používána k reprezentaci „rysů“ reálného světa v aplikacích GIS.
Vektorová funkce může mít typy „geometrie“ „bod“, „linii“ nebo „polygon“.
Každý vektorový objekt mát „atributová data“, které ho popisují.
Funkce geometrie je popsána v podímkách „vrcholů“.
Geometrie bodu je vytvořena pro „každý vrchol“ zvlášť (X, Y někdy i Z souřadnicí).
Geometrie křivky je vytvořena pro „dva a více“ vrcholů formujících danou linii.
Geomtrie polygonu je vytvořena „nejméně pro řtyři vrcholy“, které vytvářejí uzavřenou oblast. První a poslední vrchol jsou vždy na stejném místě.
Výběr, kterou geometrii použít závisí na měřítku, vhodnosti and na tom co chcetes těmito daty dále v aplikacích GIS provádět.
Většína aplikací GIS nepovoluje spojení více geometrických typů v jedné vrstvě.
Digitalizace je proces vytváření digitálních vektorových dat kreslením v aplikaci GIS.
Vektorová data mohou mít problémy s kvalitou, jako jsou „nedotahy“, „přetahy a „nedokonalosti“ které budete muset brát na vědomí.
Vektorová data mohou být použita „pro prostorovou analýzu“ v aplikacích GIS, například najít nejbližší nemocnici ke škole.
We have summarised the GIS Vector Data concept in Figure Obr. 3.41.
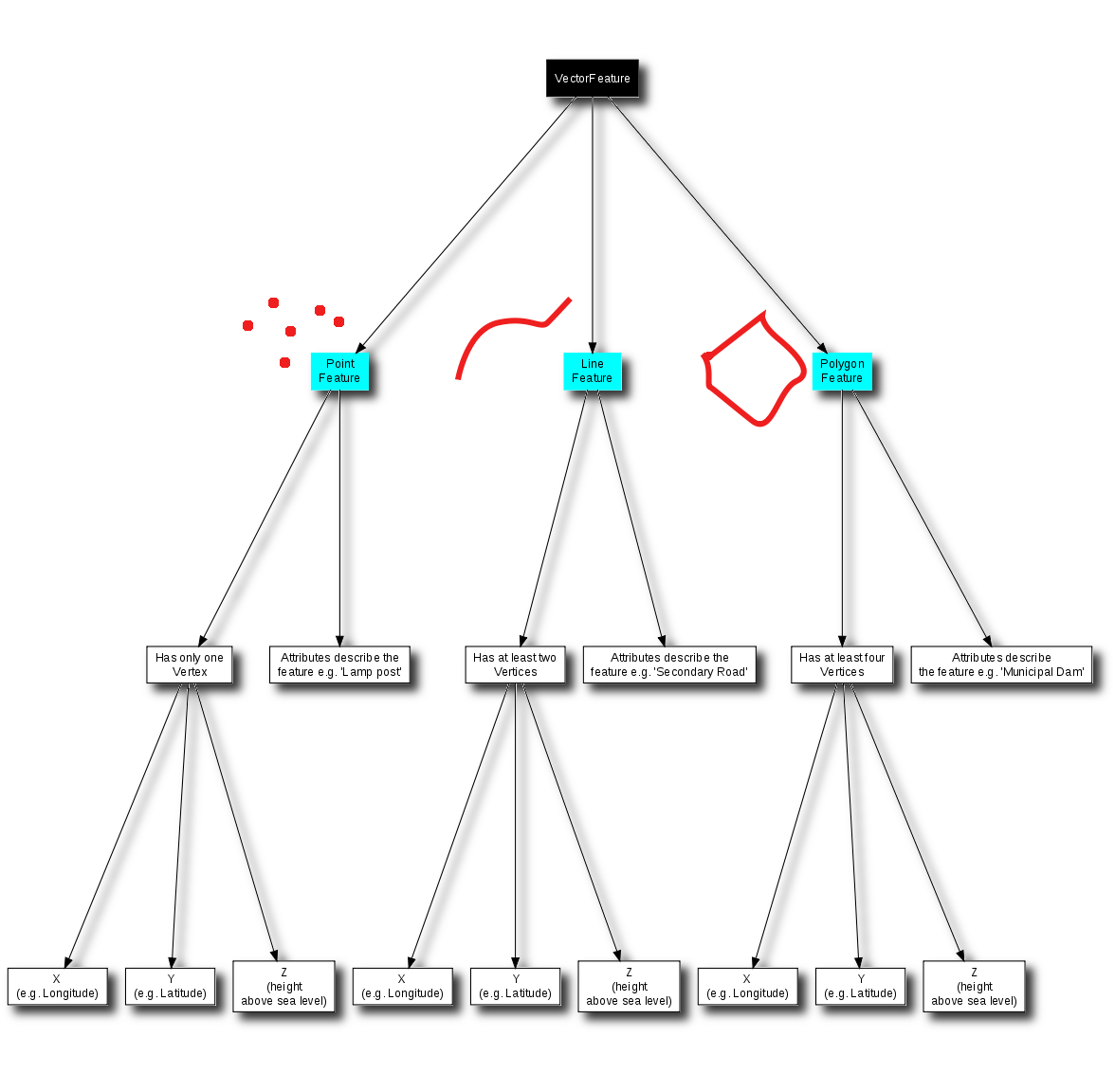
Obr. 3.41 Diagram ukazuje jak se chovají vektorová data v GIS aplikacích.
3.12. Nyní si to zkuste sami!
Zde jsou pro Vás nějaké nápady, jak si to zkusit se svými učni.
Using a copy of a toposheet map for your local area (like the one shown in Obr. 3.42), see if your learners can identify examples of the different types of vector data by highlighting them on the map.
Přemýšlejte o tom, jak byste vytvořili vektorovou funkci GIS, aby reprezentovala reálnou funkci na svých školních pozemcích. Vytvořte tabulku různých funkcí kolem vaší školi a pak dotazte své studenty, aby rozhodli, zda by bylo nejlépe zastoupeny v GIS jako bod, linie nebo polygonu. Viz table_vector_1 pro příklad.
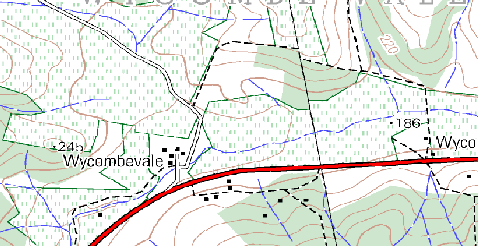
Obr. 3.42 Můžete identifikovat dvě bodové funkce a jednu polygonovou na této mapě?
Rys reálného světa |
Vhodný typ geomtrie |
|---|---|
Školní stožár |
|
Fotbalové hřiště |
|
Chodníky v a okolo školy |
|
Místa, kde se nacházejí kohoutky |
|
Atd. |
Vektorová tabulka 1: Vytvořte tabulku podle vzoru (nechte výstupní sloupec pro geomtrii prázdný) a zeptejte se žáků aby rozhodli jaký by byl vhodný geometrický objekt.
3.13. Něco k zamyšlení
Pokud nemáte k dispozici počítač můžete použít topografickou mapu a transparentní listy aby jste ukázal žákům vektorová data.
3.14. Další k přečtení
Uživatelský manuál QGIS má také více detailních informací o práci s vektorovými daty v QGIS.
3.15. Co dále?
V části, která následuje se blíže podíváme na „atributová data“ aby jsme viděli, jak můžou být použity k popisu vektorvých funkcí.
