Importante
A tradução é um esforço comunitário você pode contribuir. Esta página está atualmente traduzida em 89.83%.
11. Análise Espacial (Interpolação)
Objetivos |
Entedimento da interpolação como parte da análise espacial |
|
Palavras chave: |
Dados de ponto, métodos de interpolação, Ponderação pelo Inverso da Distância, Rede de Triângulos Irregulares. |
11.1. Visão Geral
Análise espacial é o processo de manipulação de informações espaciais para extrair novas informações e significados a partir dos dados originais. Normalmente, a análise espacial é executada com um Sistema de Informação Geográfica (SIG). Um SIG normalmente fornece ferramentas de análise espacial para calcular as estatísticas de recursos e realização de atividades de geoprocessamento como interpolação de dados. Em hidrologia, os usuários provavelmente irão enfatizar a importância da análise do terreno e modelagem hidrológica (modelar o movimento da água sobre e no terreno). Na gestão da vida selvagem, os usuários estão interessados em funções analíticas que tratam de pontos de localização de vida selvagem e sua relação com o meio ambiente. Cada usuário terá coisas diferentes em que eles estão interessados, dependendo do tipo de trabalho que exercem.
11.2. Interpolação espacial em detalhes
Spatial interpolation is the process of using points with known values to estimate values at other unknown points. For example, to make a precipitation (rainfall) map for your country, you will not find enough evenly spread weather stations to cover the entire region. Spatial interpolation can estimate the temperatures at locations without recorded data by using known temperature readings at nearby weather stations (see Fig. 11.47). This type of interpolated surface is often called a statistical surface. Elevation data, precipitation, snow accumulation, water table and population density are other types of data that can be computed using interpolation.
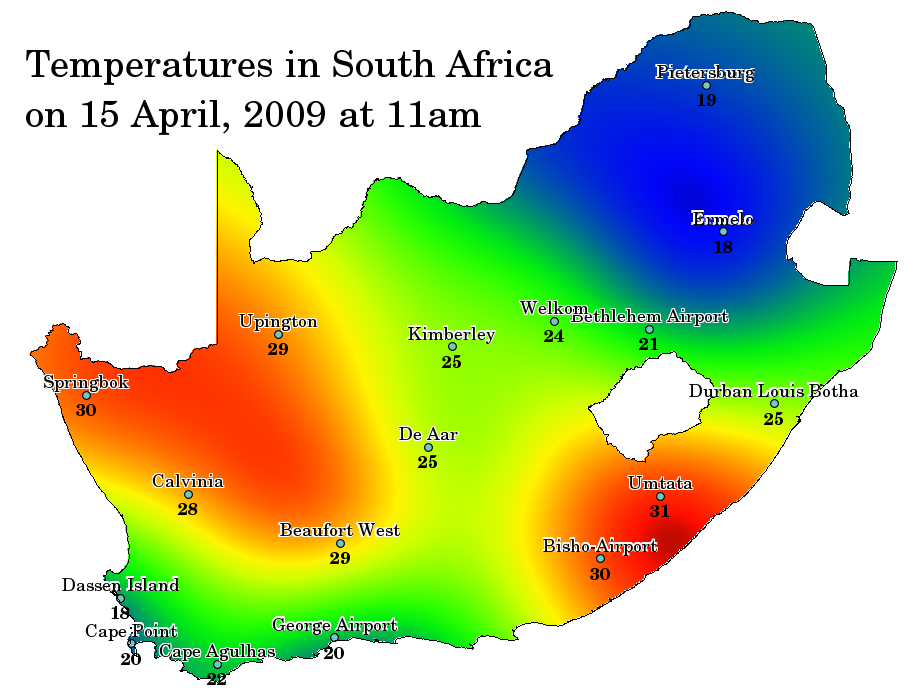
Fig. 11.47 Mapa de temperaturas interpolado das Estações Meteorológicas da África do Sul
Por causa do alto custo e recursos limitados, a coleta de dados é geralmente realizada apenas em um número limitado de pontos locais selecionados. Em SIG, a interpolação espacial destes pontos pode ser aplicada para criar uma superfície raster com estimativas feitas para todas as células deste raster.
A fim de gerar um mapa contínuo, como por exemplo, um mapa digital de elevação a partir de pontos de elevação obtidos com um dispositivo de GPS, um método apropriado de interpolação deve ser usado para melhor estimar os valores nos locais onde não foram tomados amostras ou medidas. Os resultados da análise da interpolação podem então ser utilizados para análises que cobrem toda a área e para a modelagem.
Existem muitos métodos de interpolação. Nesta introdução apresentaremos dois dos mais usados, “Inverso da Distância à Potência” (IDW) e “Redes de Triangulação Irregular” (TIN). Se você busca outros métodos de interpolação, por favor, veja na seção “Leitura adicional” no final deste tópico.
11.3. Ponderação pelo Inverso da Distância (IDW)
In the IDW interpolation method, the sample points are weighted during interpolation such that the influence of one point relative to another declines with distance from the unknown point you want to create (see Fig. 11.48).
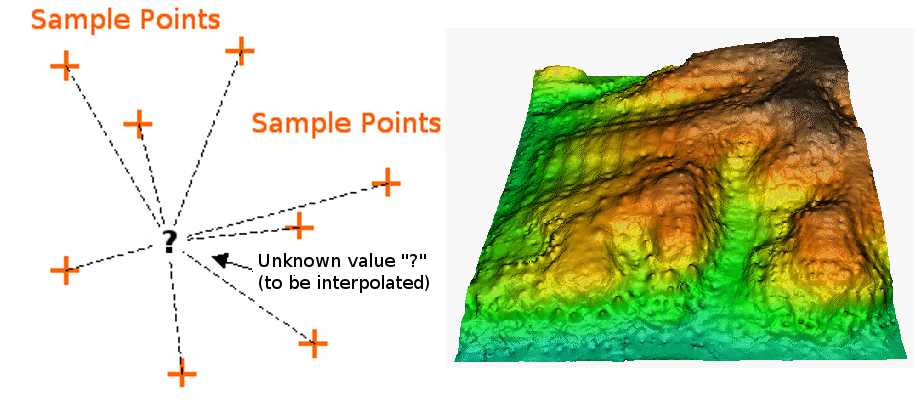
Fig. 11.48 A interpolação Ponderação pelo Inverso da Distância IDW é baseada na distância ponderada de um ponto amostral (à esquerda). Superfície IDW interpolada a partir de pontos vetoriais de elevação (à direita). Fonte da Image: Mitas, L., Mitasova, H. (1999).
A Ponderação é atribuída a pontos amostrais através da utilização de um coeficiente de ponderação que controla como a influência da ponderação irá diminuir a medida que a distância a partir do ponto desconhecido aumenta. Quanto maior for o coeficiente de ponderação, sobre menos pontos terá efeito, quanto mais longes do ponto desconhecido durante o processo de interpolação. Aumentando o coeficiente, o valor do ponto desconhecido será mais próximo ao valor dos pontos vizinhos observados.
It is important to notice that the IDW interpolation method also has some disadvantages: the quality of the interpolation result can decrease, if the distribution of sample data points is uneven. Furthermore, maximum and minimum values in the interpolated surface can only occur at sample data points. This often results in small peaks and pits around the sample data points as shown in Fig. 11.48.
In GIS, interpolation results are usually shown as a 2 dimensional raster layer. In Fig. 11.49, you can see a typical IDW interpolation result, based on elevation sample points collected in the field with a GPS device.
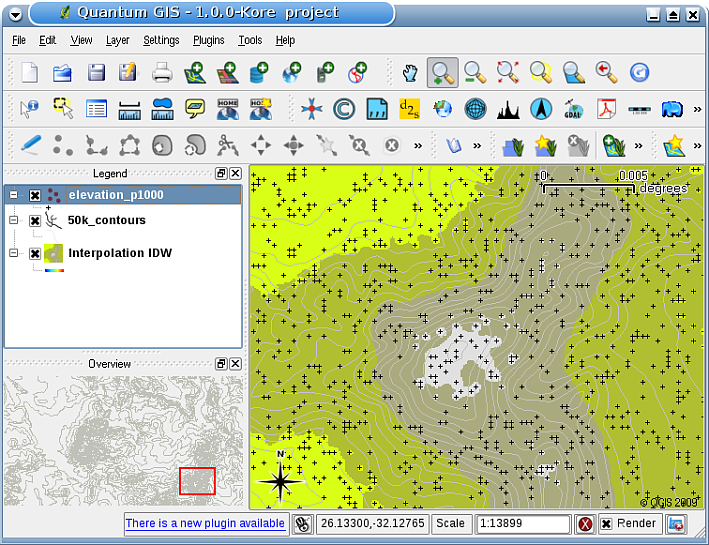
Fig. 11.49 Interpolação IDW resultante da coleta irregular de pontos amostrais com valores de elevação (mostrados como cruzes negras).
11.4. Malha Irregular Triangulada (TIN)
TIN interpolation is another popular tool in GIS. A common TIN algorithm is called Delaunay triangulation. It tries to create a surface formed by triangles of nearest neighbour points. To do this, circumcircles around selected sample points are created and their intersections are connected to a network of non overlapping and as compact as possible triangles (see Fig. 11.50).
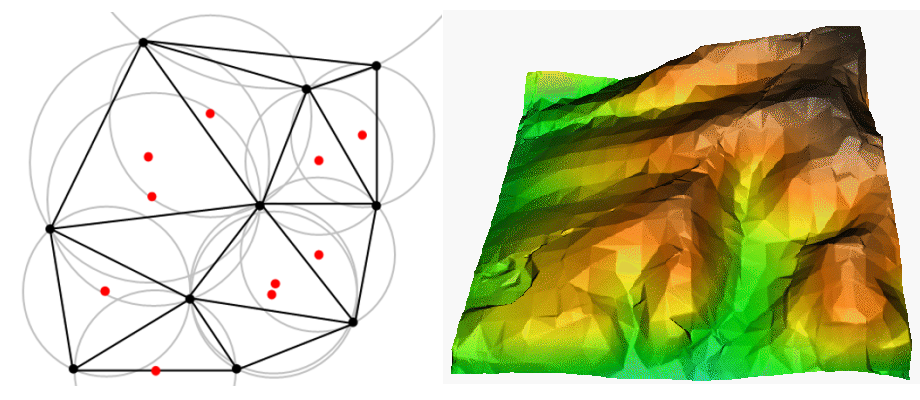
Fig. 11.50 A triangulação Delaunay com circunferências circunscritas em torno dos dados da amostra vermelho. A superfície TIN resultante interpolada criada a partir dos pontos vetoriais de de elevação é mostrada à direita. Fonte da Imagem: Mitas, L., Mitasova, H. (1999).
The main disadvantage of the TIN interpolation is that the surfaces are not smooth and may give a jagged appearance. This is caused by discontinuous slopes at the triangle edges and sample data points. In addition, triangulation is generally not suitable for extrapolation beyond the area with collected sample data points (see Fig. 11.51 ).
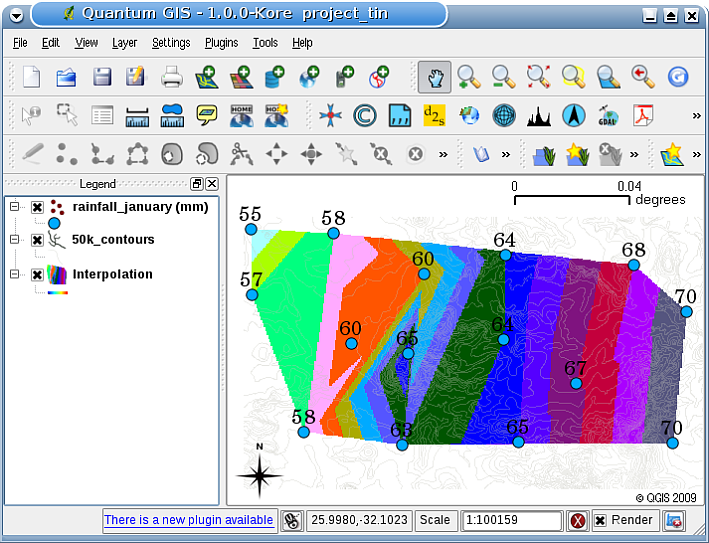
Fig. 11.51 Resultado da interpolação Delaunay TIN a partir de pontos amostrais com dados pluviais (círculos azuis)
11.5. Problemas comuns / coisas que devemos estar cientes
É importante relembrar que não há um método de interpolação que pode ser aplicado à qualquer situação. Alguns são mais exatos e úteis que outros mas demoram muito para realizar o cálculo. Todos tem suas vantagens e desvantagens. Na prática, a escolha de uma método particular de interpolação dependerá da qualidade do dados amostrais, do tipo de superfície que será gerada e a tolerância aos erros estimados. Geralmente, um procedimento de três passos é recomendado:
Avaliar os dados da amostra. Faça isso para ter uma idéia de como os dados são distribuídos na área, uma vez que pode fornecer pistas sobre qual método de interpolação deverá usar.
Aplicar um método de interpolação que é mais adequado para ambos, os dados da amostra e os objetivos do estudo. Quando você estiver em dúvida, tente vários métodos, se disponível.
Compare os resultados e encontre o melhor resultado e o método mais adequado. Isso pode parecer um processo demorado no início. No entanto, a medida que você ganha experiência e conhecimento de diferentes métodos de interpolação, o tempo necessário para a geração de superfície mais adequado será bastante reduzido.
11.6. Outros métodos de interpolação
Embora nós nos concentramos nos métodos de interpolação IDW e TIN nesta abordagem, há mais métodos de interpolação espaciais em SIG, como Splines Regulares com Tensão (RST), ou inteporlação por Krigagem ou Superfície de Tendência. Veja informações adicionais no link web abaixo.
11.7. O que aprendemos?
Para encerar vamos ver o que abordamos na lista abaixo:
Interpolação utiliza pontos vetoriais com valores conhecidos para estimar valores locais desconhecidos cobrindo a superfície de toda uma área.
O resultado da interpolação é tipicamente uma camada raster.
É importante encontrar um método de interpolação adequado que otimize a estimativa de valores locais desconhecidos.
Interpolação IDW atribui pesos ponderados aos pontos amostrais, de modo que a influência de um ponto sobre outro diminui com a distância do novo ponto a ser estimado.
Interpolação TIN utiliza pontos de amostragem para criar uma superfície formada por triângulos com base em informações do ponto de vizinho mais próximo.
11.8. Agora é sua vez de tentar!
Aqui estão algumas idéias para você experimentar com os seus alunos:
O Departamento de Agricultura planeja cultivar novas terras em sua região, mas além da classificação dos solos, eles querem saber se a incidência de chuva é suficiente para uma boa colheita. Toda a informação que eles têm disponível vem de algumas estações meteorológicas ao redor da área. Crie uma superfície interpolada com os seus alunos que demostre quais áreas são susceptíveis de receber a maior precipitação.
O escritório de turismo quer publicar informações sobre as condições do tempo em janeiro e fevereiro. Eles têm os dados de temperatura, precipitação e da velocidade do vento e pediram-lhe para interpolar os seus dados para estimar lugares onde os turistas provavelmente terão condições meteorológicas ideais com temperaturas amenas, nenhuma chuva e pouca incidência do vento. Você consegue identificar as áreas em sua região que atendem a esses critérios?
11.9. Algo para se pensar
Se você não tiver um computador disponível, você pode usar uma caderneta de campo e uma régua para estimar valores de elevação entre curvas de nível ou valores de precipitação entre estações meteorológicas de fictícias. Por exemplo, se as chuvas na estação meteorológica A é de 50 mm por mês e na estação meteorológica B é 90 mm, você pode estimar que a precipitação na metade da distância entre a estação meteorológica A e B é de 70 mm.
11.10. Leitura complementar
Livros:
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005): Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Mitas, L., Mitasova, H. (1999). Spatial Interpolation. In: P.Longley, M.F. Goodchild, D.J. Maguire, D.W.Rhind (Eds.), Geographical Information Systems: Principles, Techniques, Management and Applications, Wiley.
Websites:
O Guia do Usuário QGIS também possui mais informações detalhadas sobre as ferramentas de interpolação fornecidas no QGIS.
11.11. Qual é o próximo?
Este é o encarte final desta série. Nós encorajamos você a explorar o QGIS e usar o manual que o acompanha para descobrir todas as outras coisas que você pode fazer com o software SIG!
