Important
La traduction est le fruit d’un effort communautaire auquel vous pouvez vous joindre. Cette page est actuellement traduite à 100.00%.
8. Systèmes de Coordonnées de Référence
Objectifs : |
Comprendre les Systèmes de Coordonnées de Référence |
|
Mots clés : |
Système de Coordonnées de Référence (SCR), Projection de carte, Projection à la volée, Latitude, Longitude, Ordonnée, Abscisse |
8.1. Aperçu
Les projections cartographiques tentent de figurer la surface terrestre, ou une portion de celle-ci, sur une feuille de papier à plat or sur l’écran d’un ordinateur. En clair, les projections cartographiques tentent de transformer la forme sphérique (3 dimensions) de la Terre en une forme plane (2 dimensions).
Un système de coordonnées de référence (SCR) est ce qui définit la relation entre la carte projetée en deux dimensions dans votre SIG et les lieux réels sur la Terre. Le choix d’une projection cartographique et d’un SCR dépend de l’emprise de votre zone d’étude, des analyses que vous souhaitez faire, et souvent des données disponibles.
8.2. Projection Cartographique en détail
Une méthode traditionnelle pour représenter la terre est d’user de globes terrestres. Cependant, ceci pose un problème au niveau de l’approche. Bien que les globes terrestres conservent la majorité de forme de la terre et montrent la configuration spatiale et la taille des continents, ils sont difficilement transportables. Ils sont aussi peu pratiques à utiliser à de très petites échelles (ex : 1:100 millions).
La plupart des données de cartes thématiques utilisées couramment dans les applications SIG ont une échelle plus grande. L’ensemble de données typiques SIG ont des échelles de 1:250 000 ou plus, en fonction du niveau des détails. Un globe de cette taille serait compliqué et coûteux à produire, et encore plus à transporter. En conséquence, les cartographes ont développés un ensemble de techniques appelé projections cartographiques servant à montrer, avec une précision raisonnable, la terre sphérique en deux dimensions.
Lorsque l’on voit la terre depuis la terre, elle semble être plate. Cependant, lorsqu’on la regarde depuis l’espace, on constate qu’elle est sphérique. Les cartes, comme nous le verrons dans le prochain sujet de production de cartes, sont des représentations de la réalité. Elles ne servent pas juste à représenter les apparences, mais aussi les formes et les dispositions géographiques. Chaque projection cartographique a des avantages et des désavantages. La meilleure projection d’une carte dépend de l’échelle de la carte, et pour l’objectif pour laquelle elle sera utilisée. Par exemple, une projection peut avoir des distorsions inacceptables si elles sont utilisées pour cartographier l’ensemble du continent africain, mais peut être un excellent choix pour une carte à grande échelle (détaillée) de votre pays. Les propriétés d’une projection cartographique peut aussi influencer certaines caractéristiques de conception de la carte. Certaines projections sont bonnes pour de petites zones, d’autres pour cartographier une large étendue Est-Ouest et d’autres sont bonnes pour cartographier des zones avec une grande étendue Nord-Sud.
8.3. Les trois familles de projections cartographiques
Le processus pour la création de projection d’une carte peut être visualisé en positionnant une source de lumière à l’intérieur d’un globe transparent, sur lequel sont placés les éléments de la terre. Puis projeter le résultat à plat sur une feuille de papier. Différentes projections peuvent être produites en entourant le globe par un cylindre, un cône ou même une surface plane. Chacune de ces méthodes fournit ce que l’on appelle un ensemble de projections cartographiques. Par conséquent, il y a un ensemble de projections planaires, de projections cylindriques et enfin de projections coniques (voir Fig. 8.43)

Fig. 8.43 Les trois familles de projections cartographiques. On peut les regrouper en a) projections cylindriques, b) projections coniques ou c) projections planes ou azimutales.
Aujourd’hui, bien sur, la méthode de projection d’une zone courbe sur un plan utilise les théorèmes mathématiques de la géométrie de la trigonométrie. Pour imaginer ce procédé, on place une lampe au centre d’un globe et on regarde l’image projetée de ce globe sur une feuille de papier.
8.4. Précision des projections cartographiques
Les projections cartographiques ne sont jamais une représentation absolument exacte de la Terre. À chaque projection, les cartes affichent des distorsions sur la conformité des angles, des distances et des surfaces. Une projection cartographique peut combiner plusieurs de ces caractéristiques, ou peut être un compromis entre ces déformations de surface, de distance et d’angle, dans des limites raisonnables. Par exemple, la projection de Winkel-Tripel et la projection de Robinson (voir Fig. 8.44), sont souvent utilisées pour produire et visualiser les cartes du monde.
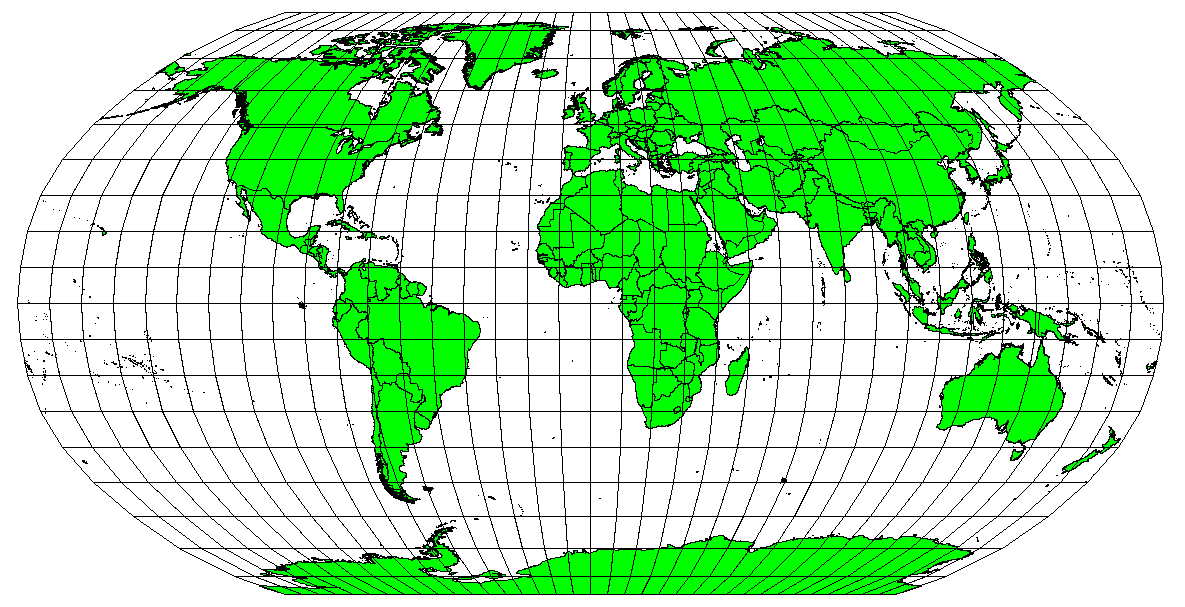
Fig. 8.44 La projection Robinson est un compromis où les distorsions d’aires, la conservation des angles et des distances sont acceptables.
La plupart du temps, il est impossible de conserver à la fois toutes les caractéristiques d’une projection cartographique. Cela signifie que lorsque vous aurez besoin de précisions sur des opérations d’analyse, il vous faudra choisir une projection adaptée à vos besoins. Par exemple, si vous avez besoin de mesurer les distances sur une carte, vous devriez essayer une projection qui fournit une haute précision pour les distances.
8.4.1. Projection conservant les angles
Lorsque l’on travaille sur un globe, les principales directions d’une rose des vents (Nord, Sud, Est, Ouest) se situeront toujours à 90 degrés d’une autre. En d’autres termes, l’Est sera toujours à 90 degrés du Nord. Le maintien correct des propriétés angulaires peut ainsi être préservé sur certaines projections. Une projection qui conserve ces propriétés d’angle est appelée conforme ou projection orthomorphique.
Ces projections sont utilisées lorsque la relation de conservation des angles est importante. Elles sont souvent employées à des fins de navigation ou de météorologie. Il est important de se rappeler que le maintien correct des angles sur une carte est assez difficile sur de larges surfaces et devraient donc être gardées pour des petites zones. La projection conforme résulte dans la déformation des surfaces, signifiant que si les mesures sont effectuées sur la carte, elles seront incorrectes. Une plus grande surface aura donc de plus grandes erreurs de mesure. Il en va ainsi pour la projection Mercator (comme présentée dans Fig. 8.45) et la projection Conique conforme de Lambert. Le U.S. Geological Survey utilise une projection conforme pour plusieurs de ses cartes topographiques.
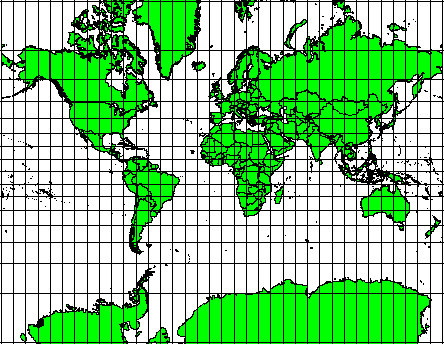
Fig. 8.45 La projection Mercator, par exemple, est utilisée lorsque le respect des angles est important. Cependant, elle ne respecte pas les surfaces.
8.4.2. Projection conservant les distances
Si votre but en projetant une carte est de mesurer précisément des distances, vous devriez sélectionner une projection qui est désignée pour bien préserver des distances. Ces projections, appelées projections équidistantes, demandent que l”échelle de la carte soit maintenue constante. Une carte est équidistante lorsqu’elle représente correctement des distances depuis le centre de la projection à un autre endroit sur la carte. Les Projections équidistantes maintiennent des distances précises depuis le centre de la projection ou le long de lignes données. Ces projections sont utilisées pour la radio et la cartographie sismique, et pour la navigation. La projection Plate Carrée Cylindrique Équidistante (voir Fig. 8.46) et la Projection équirectangulaire sont deux bons exemples de projections équidistantes. La Projection azimutale équidistante est la projection utilisée pour l’emblème des Nations Unies (voir Fig. 8.47).

Fig. 8.46 La projection Plate Carrée Cylindrique Équidistante est, par exemple, utilisée lorsque la mesure précise de la distance est importante.

Fig. 8.47 Sur le logo des Nations Unies, on peut voir une représentation symbolique d’une projection Azimutale Équidistante.
8.4.3. Projections respectant les surfaces
Quand une carte affiche des zones dont la superficie est proportionnelle à celles des zones réelles sur Terre qui sont représentées, on dit que la carte respecte les surfaces. Ainsi, en pratique, les cartes de référence ou à but éducatif utilisent le plus souvent des projections respectant les surfaces, ou projections équivalentes. Comme le nom l’indique, ces cartes sont utiles quand vous faites surtout des calculs de superficie. Si, par exemple, vous analysez une zone dans votre commune pour vérifier si elle est suffisamment grande pour accueillir un centre commercial, les projections respectant les surfaces sont à préférer. Avec ces projections, plus la zone à étudier est grande, plus les mesures de superficies seront précises. Par contre, une projection respectant les surfaces déformera les angles, d’autant plus que la zone d’étude est grande. Les angles des petites surfaces sont beaucoup moins déformés par une projection équivalente. La projection d’Albers, la projection azimutale équivalent de Lambert et la projection de Mollweide (Fig. 8.48) sont des exemples de projections respectant les surfaces souvent utilisées dans les travaux SIG.
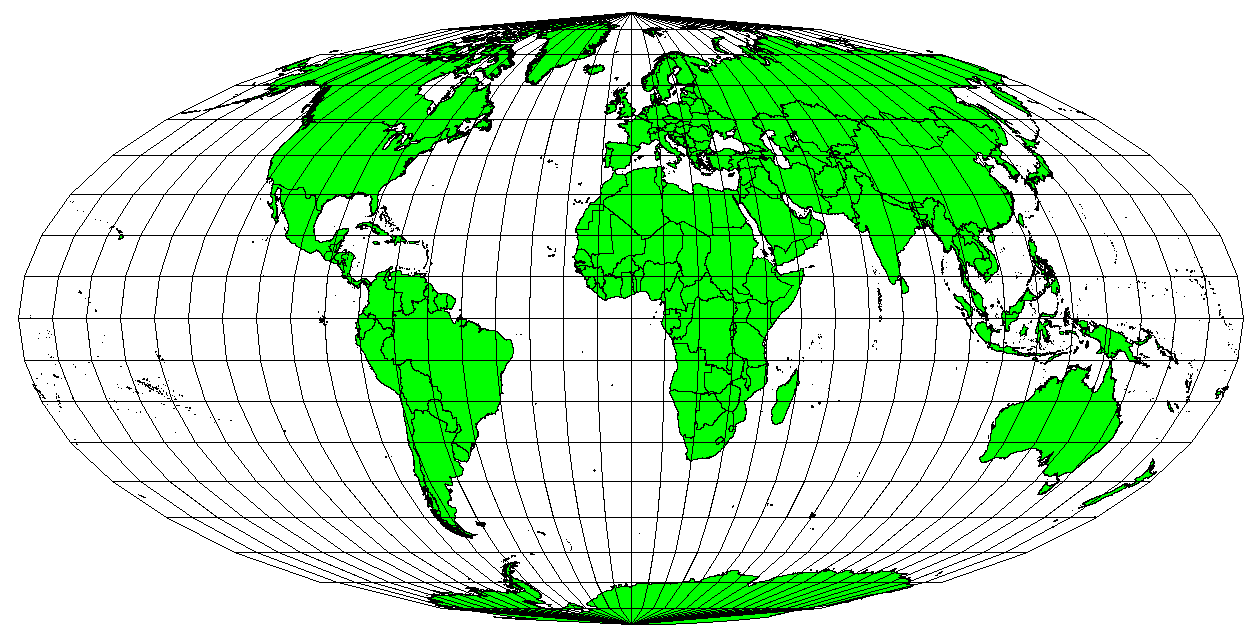
Fig. 8.48 Par exemple, la projection Mollweide Cylindrique de Surface Égale assure que toutes les zones cartographiées ont la même relation proportionnelle aux zones de la Terre.
Gardez en tête que la projection de carte est un sujet très complexe. Il y a des centaines de projections différentes disponibles dans le monde, chacun essayant de représenter une certaine portion de la surface de la terre aussi fidèlement que possible sur une feuille de papier plate. En réalité, le choix de quelle projection utiliser sera souvent fait par vous. La plupart des pays ont communément utilisé des projections et lorsque les données sont échangées, les gens vont suivre la tendance nationale.
8.5. Système de Coordonnées de Référence (SCR) en détail
Grâce aux systèmes de coordonnées de référence (SCR), chaque point de la terre peut être spécifié par un ensemble de trois nombres, appelés coordonnées. En général, les SCR se divisent en systèmes de coordonnées de référence projetées (aussi appelés systèmes de coordonnées de référence cartésiennes ou rectangulaires) et systèmes de coordonnées de référence géographique.
8.5.1. Systèmes de Coordonnées Géographiques
L’utilisation des Systèmes de Coordonnées Géographique est très courante. Pour définir un point à la surface de la Terre, ils utilisent la Latitude et la Longitude qui s’expriment en degrés, et parfois une valeur de hauteur est donnée en plus. Le plus connu et le plus utilisé est le WGS 84.
Les Lignes de latitude courent parallèlement à l’équateur et divisent la terre en 180 sections séparées de manière égale du Nord au Sud (ou du Sud au Nord). La ligne de référence pour la latitude est l’équateur et chaque hémisphère est divisé en quatre-vingt-dix sections, chacune représentant un degré de latitude. Dans l’hémisphère nord, les degrés de latitude sont mesurés depuis zéro à l’équateur jusqu’à quatre-vingt-dix au pôle nord. Dans l’hémisphère sud, les degrés de latitude sont mesuré depuis zéro à l’équateur jusqu’à quatre-vingt-dix au pôle sud. Pour simplifier la digitalisation des cartes, les degrés de latitude dans l’hémisphère sud sont souvent assignés à des valeurs négatives (0 à -90°). Peu importe où vous vous trouvez sur la surface terrestre, la distance entre les lignes de latitude est la même (60 miles nautiques). Voir Fig. 8.49 pour une vue en perspective.
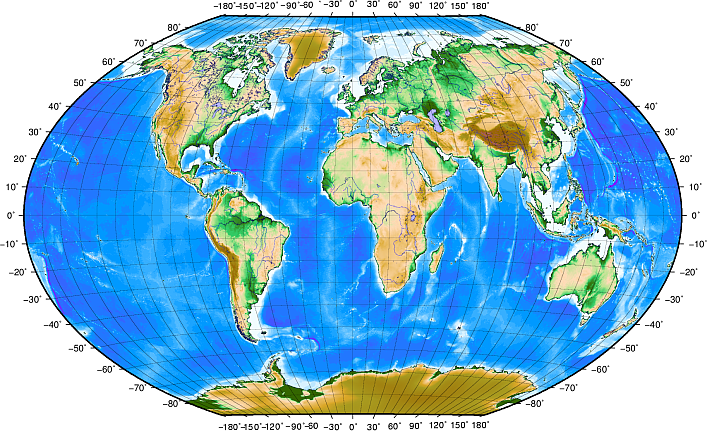
Fig. 8.49 Les Systèmes de Coordonnées Géographiques avec des lignes de Latitude, parallèles à l’équateur, et des lignes de Longitude, qui démarrent avec le méridien de Greenwich (à côté de Londres)
Les Lignes de longitude, d’autre part, ne résistent pas aussi bien à la norme d’uniformité. Les lignes de longitude courent perpendiculairement à l’équateur et convergent aux pôles. La ligne de référence pour la longitude (le méridien) court du Pôle Nord au Pôle Sud via Greenwich en Angleterre. Les lignes successives de longitude sont mesurées de zéro jusqu’à 180 degrés à l’Est ou à l’Ouest du méridien. Notez que les valeurs à l’Ouest du méridien sont assignées à des valeurs négatives à utiliser dans des applications de cartographie digitale. Voir Fig. 8.49 pour une vue en perspective.
À l’équateur, et seulement à l’équateur, la distance représentée par une ligne de longitude est égale à la distance représentée par un degré de latitude. Lorsque vous vous déplacez vers les pôles, la distance entre les lignes de longitude devient progressivement moins grande, jusqu’à ce que, à l’exacte position du pôle, les 360° de longitude soient représentés par un unique point sur lequel vous pouvez mettre votre doigt (même si vous auriez probablement envie de porter des gants). En utilisant le système de coordonnées géographiques, nous avons une grille de lignes divisant la terre en carrés qui couvrent approximativement 12363.365 kilomètres carrés à l’équateur — un bon départ, mais pas très utile pour déterminer la localisation de n’importe quoi d’autre sans ce carré.
Pour être vraiment utile, une grille de carte doit être divisée en suffisamment de petites sections de sorte qu’elles puissent être utilisées pour décrire (avec un niveau acceptable de précision) l’emplacement d’un point sur la carte. Pour faire ceci, les degrés sont divisés en minutes (') et secondes ("). Il y a soixante minutes dans un degré, et soixante secondes dans une minute (3600 secondes dans un degré). Donc, à l’équateur, une seconde de latitude ou de longitude = 30.87624 mètres.
8.5.2. Système de Coordonnées de Référence Projeté
Un système de coordonnées de référence à deux dimensions est communément défini par deux axes. À angle droit l’un de l’autre, ils forment ce qu’on appelle un plan XY (voir Fig. 8.50 sur le côté gauche). L’axe horizontal est normalement étiqueté X, et l’axe vertical est normalement étiqueté Y. Dans un système de coordonnées de référence à trois dimensions, un autre axe, normalement étiqueté Z, est ajouté. Il est aussi à angle droit avec les axes X et Y. L’axe Z fournit la troisième dimension de l’espace (voir Fig. 8.50 sur le côté droit). Chaque point qui est exprimé en coordonnées sphériques peut être exprimé comme une coordonnée X Y Z.
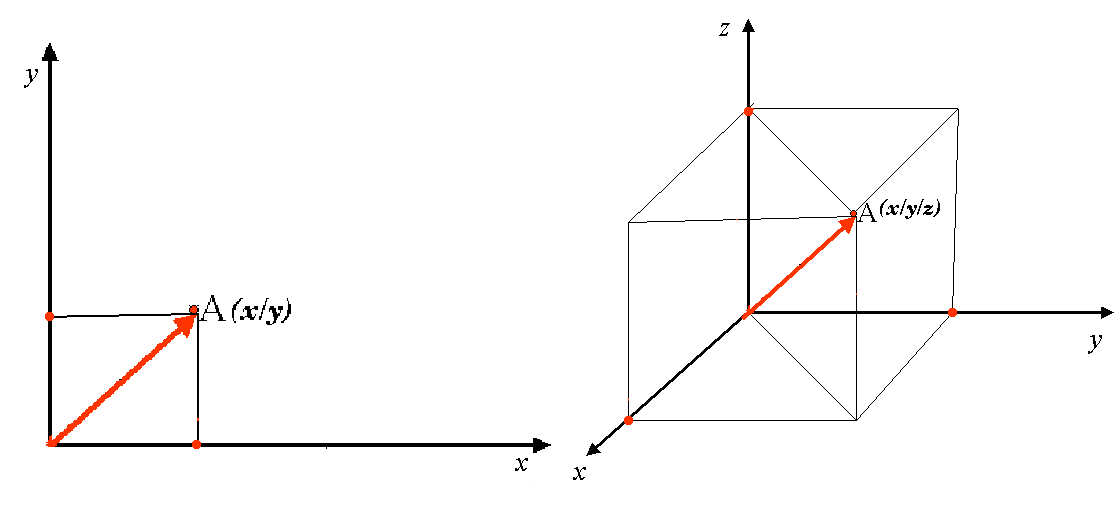
Fig. 8.50 Système de Coordonnées de Référence à deux ou trois dimensions
Un système de coordonnées de référence projeté dans l’hémisphère sud (sud de l’équateur) a normalement son origine sur l’équateur à une Longitude spécifique. Cela signifie que les valeurs Y augmentent vers le sud et que les valeurs X augment vers l’Ouest. Dans l’hémisphère nord (nord de l’équateur), l’origine est aussi l’équateur à une Longitude spécifique. Cependant, les valeurs Y augmentent maintenant vers le nord et les valeurs X augmentent vers l’Est. Dans la section suivante, nous décrivons un système de coordonnées de référence projeté, appelé Transverse Universelle de Mercator (UTM, en anglais Universal Transverse Mercator), souvent utilisé pour l’Afrique du Sud.
8.6. Transverse Universelle de Mercator (UTM) en détail
Le système de coordonnées de référence Transverse Universelle de Mercator (UTM) a pour origine l”équateur et une longitude particulière. Cette fois, les coordonnées Y augmentent vers le Sud et les coordonnées X augmentent vers l’Ouest. Le SCR UTM est un système mondial. Cela signifie qu’il est utilisé en général pour représenter le monde entier. Mais, comme décrit dans la section « Précision des projections cartographiques » plus haut, plus la zone d’étude est grande (l’Afrique du Sud par exemple), plus les angles, les distances et les surfaces sont déformés. Pour éviter de trop grandes déformations, le monde est divisé en 60 zones égales qui sont toutes larges de 6 degrés en longitude, d’Est en Ouest. Ces zones UTM sont numérotées de 1 à 60 à partir de celle antéméridienne (la zone 1 se trouve à 180 degrés Ouest de longitude) et en allant vers l’Est (la zone 60 est à 180 degrés Est de longitude), ainsi que le montre la figure Fig. 8.51.
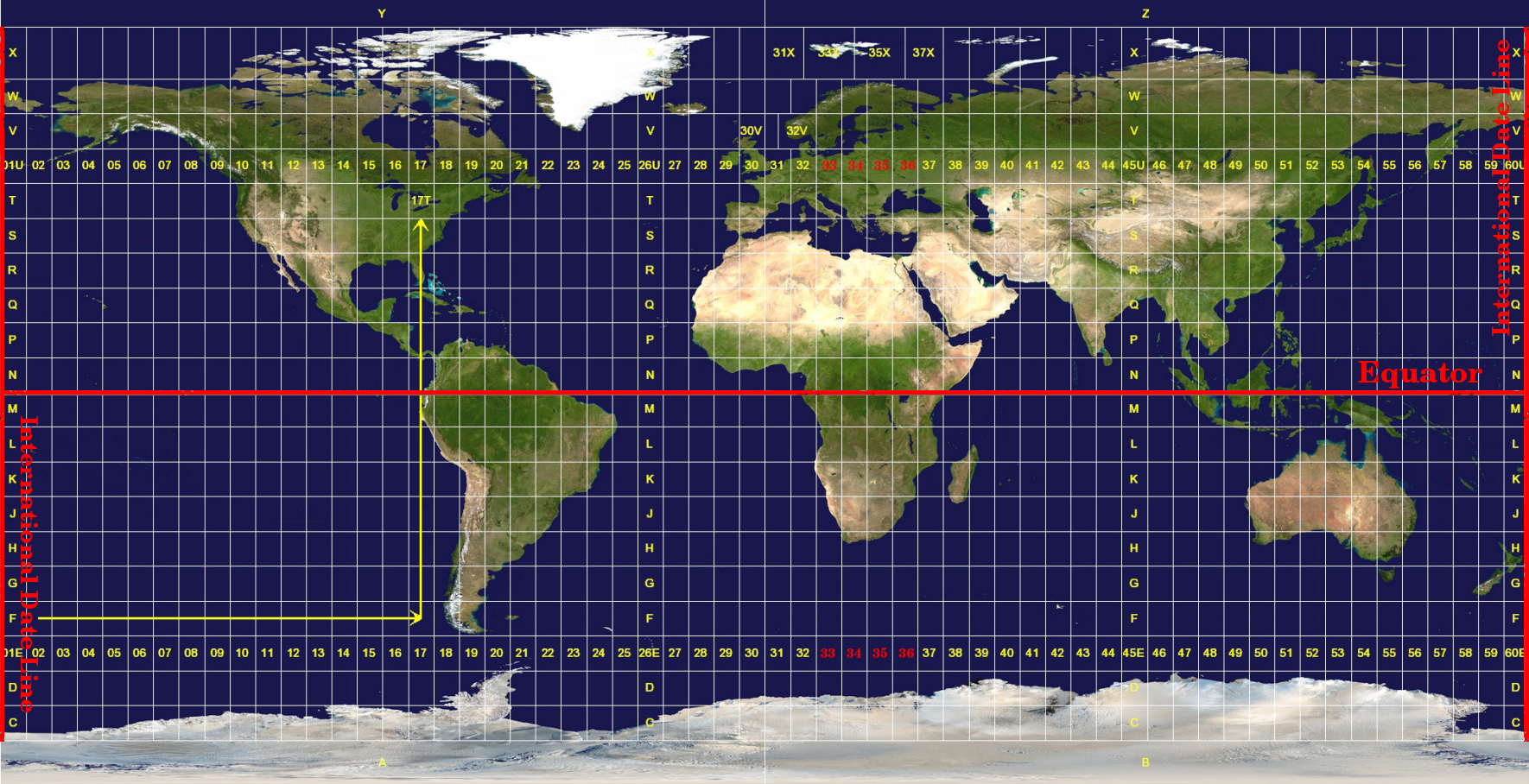
Fig. 8.51 Les zones Universal Transverse Mercator. Pour l’Afrique du Sud, les zones UTM 33S, 34S, 35S et 36S sont utilisées.
Comme vous pouvez le voir sur les figures Fig. 8.51 et Fig. 8.52, l’Afrique du Sud est couverte par quatre zones UTM pour minimiser les déformations. Ces zones sont appelées UTM 33S, UTM 34S, UTM 35S et UTM 36S. Le S après la zone signifie que les zones UTM sont situées au sud de l’équateur.
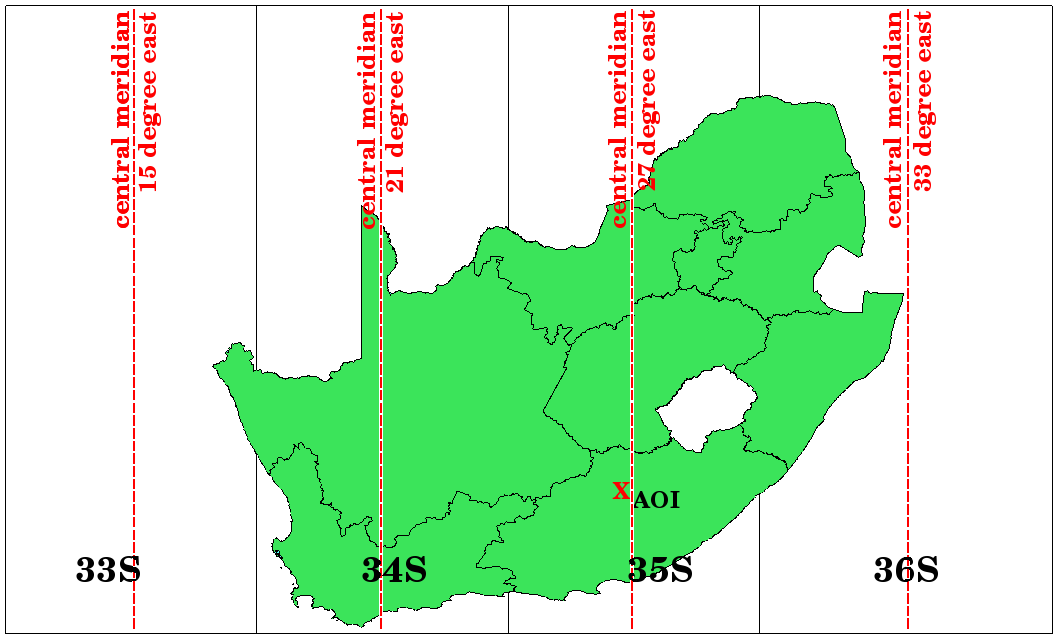
Fig. 8.52 Les Projections UTM 33S, 34S, 35S et 36S, avec leur longitude centrale sont utilisés pour représenter l’Afrique du Sud avec une bonne précision. La croix rouge localise une Zone d’Intérêt (ZI).
Disons, par exemple, que nous voulions définir une coordonnée à deux dimensions dans une Zone d’Intérêt (ZI) représentée par une croix dans Fig. 8.52. Vous pouvez voir que la ZI est localisée en UTM zone 35S. Cela signifie que pour minimiser les déformations et pour obtenir des résultats d’analyse spatiale, il faut utiliser le Système de Coordonnées de Référence UTM zone 35S.
La position d’une coordonnée en UTM au sud de l’équateur doit être indiquée avec le numéro de zone (35) et avec sa valeur d’ordonnée (Y) et valeur d’abscisse (X) en mètres. La valeur d’ordonnée est la distance de la position par rapport à l’équateur en mètres. La valeur d’abscisse est la distance du méridien central (longitude) de la zone UTM utilisée. Pour la zone UTM 35S, elle est de 27 degrés Est comme indiqué dans la figure Fig. 8.52. De plus, comme nous sommes au sud de l’équateur et que les valeurs négatives ne sont pas autorisées dans le système de référence de coordonnées UTM, nous devons ajouter une soi-disant fausse valeur d’ordonnée de 10 000 000 m à la valeur d’ordonnée (Y) et une fausse abscisse de 500 000 m à la valeur d’abscisse (X). Cela semble difficile, nous allons donc faire un exemple qui vous montrera comment trouver la bonne coordonnée UTM 35S pour la zone d’intérêt.
8.6.1. La valeur d’ordonnée (Y)
L’endroit que nous recherchons est à 3 550 000 mètres au sud de l’équateur, de sorte que la valeur d’ordonnée (Y) obtient un signe négatif et est de -3 550 000 m. Selon les définitions UTM, nous devons ajouter une fausse valeur d’ordonnée de 10 000 000 m. Cela signifie que la valeur d’ordonnée (Y) de notre coordonnée est de 6 450 000 m (-3 550 000 m + 10 000 000 m).
8.6.2. La valeur d’abscisse (X)
Nous devons d’abord trouver le méridien central (longitude) pour la zone UTM 35S. Comme nous pouvons le voir dans Fig. 8.52, il fait 27 degrés Est. L’endroit que nous recherchons est à 85 000 mètres à l’ouest du méridien central. Tout comme la valeur d’ordonnée, la valeur d’abscisse (X) obtient un signe négatif, donnant un résultat de - 85 000 m. Selon les définitions UTM, nous devons ajouter une fausse valeur d’abscisse de 500 000 m. Cela signifie que la valeur d’abscisse (X) de notre coordonnée est de 415 000 m (-85 000 m + 500 000 m). Enfin, nous devons ajouter le numéro de zone à la valeur d’abscisse pour obtenir la valeur correcte.
En conséquence, les coordonnées de notre Point d’Intérêt en zone 35S UTM seraient écrites comme suit : 35 415 000 m E / 6 450 000 m N. Dans certains SIG, lorsque la projection UTM zone 35S est correctement définie et que les unités sont définies en mètres dans le système, les coordonnées peuvent aussi apparaître sous la forme 415 000 , 6 450 000.
8.7. Projection à la volée
Comme vous pouvez l’imaginer il pourrait y avoir une situation où les données que vous souhaitez utiliser dans un SIG sont projetées dans des systèmes de coordonnées de référence différents. Par exemple, vous pourriez obtenir une couche vecteur montrant les limites de l’Afrique du Sud projetée en UTM 35S et une autre couche de vecteur avec des points d’informations sur les précipitations projetée dans le système de coordonnées géographiques WGS84. Dans un SIG, ces deux couches vecteurs sont placées dans des zones totalement différentes de la fenêtre de carte, parce qu’elles ont différentes projections.
Pour pallier à cela, beaucoup de SIG offrent une fonctionnalité dite de projection à la volée. Cela signifie que vous pouvez fixer une projection quand vous démarrez votre SIG et que toutes les couches que vous chargez alors, quel que soit leur système de coordonnées de référence, s’afficheront automatiquement dans la projection choisie. Cette fonctionnalité vous permet de superposer des couches dans le canevas de votre SIG bien qu’elles soient dans des systèmes de référence différents. Dans QGIS, cette fonctionnalité est activée par défaut.
8.8. Problèmes courants / Choses à savoir
Le sujet projection de la carte est très complexe et même des professionnels qui ont étudié la géographie, la géodésie et toutes autres sciences liées aux SIG ont souvent des problèmes avec la définition correcte des projections de cartes et les systèmes de coordonnées de référence. Habituellement, lorsque vous travaillez avec des SIG, vous avez déjà projeté les données pour commencer. Dans la plupart des cas, ces données seront projetées dans un certain SCR, donc vous n’avez pas besoin de créer un nouveau SCR ou même de reprojeter les données d’un SCR à un autre. Cela dit, c’est toujours utile d’avoir une idée sur ce que signifient une projection de carte et un SCR.
8.9. Qu’avons-nous appris?
Faisons le point sur ce que nous avons abordé dans cette partie :
Les « Projections de Cartes » figurent la surface de la terre sur une représentation à deux dimensions, sur une feuille de papier ou sur un écran d’ordinateur.
Il existe des projections « globales », mais la plupart des projections sont adaptées à une représentation de petites zones par rapport à la surface de la terre.
Les Projections ne donnent jamais une représentation exacte de la rotondité de la terre. « La conformité des angles, des distances et des surfaces » n’est pas toujours respecté. C’est d’ailleurs impossible de respecter toutes ces caractéristiques mathématiques à la fois sur une projection.
Un « Système de Coordonnées de Référence » (SCR) défini, avec l’aide des coordonnées, comment des lieux réels sur terre sont projetés sur un plan à deux dimensions.
Il y a deux types de systèmes de coordonnées de référence : Systèmes de Coordonnées Géographiques et Systèmes de Coordonnées Projetées.
La projection à la volée est une fonctionnalité dans les SIG qui permet de superposer des couches, même si elles sont projetées dans différents systèmes de coordonnées de référence.
8.10. Maintenant, essayez !
Voici quelques pistes d’actions à essayer avec vos élèves :
Démarrez QGIS
In cochez Aucune projection (ou projection inconnue/non-terrestre)
Chargez deux couches ayant des emprises superposées mais avec deux projections différentes
Encouragez les élèves à chercher les coordonnées de plusieurs lieux sur chaque coche. Vous pouvez leur montrer qu’il n’est pas possible de superposer les deux couches.
Maintenant choisissez le système des coordonnées de référence WGS 84 dans la fenêtre Propriétés du projet
Chargez à nouveau les deux couches aux emprises superposées et constatez avec vos élèves que d’avoir défini un SCR pour le projet (ce qui a donc activé la reprojection « à la volée ») a fonctionné.
Vous pouvez ouvrit à nouveau la fenêtre Propriétés du projet dans QGIS et montrez à vous élèves la grande quantité de systèmes de coordonnées de références afin qu’ils entrevoient la complexité de ce sujet. Vous pouvez essayer d’afficher les couches avec différents SCR.
8.11. Pour aller un peu plus loin…
Si vous n’avez pas d’ordinateur disponible, vous pouvez montrer à vos élèves les principes de trois familles de projections. Avec un globe terrestre et une feuille de papier, montrez comment les projections cylindriques, coniques et planaires fonctionnent en général. Avec une feuille de papier calque, vous pouvez dessiner une système de coordonnées de référence en deux dimensions, montrant les axes X et Y. Laissez alors vous élèves définir les coordonnées (X et Y) pour différents endroits.
8.12. Pour aller plus loin
Livres :
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X
Sites Web :
https://foote.geography.uconn.edu/gcraft/notes/mapproj/mapproj_f.html
http://geology.isu.edu/wapi/geostac/Field_Exercise/topomaps/index.htm
Le Guide de l’Utilisateur de QGIS contient également plus d’informations détaillées sur l’utilisation des projections cartographiques dans QGIS.
8.13. La suite ?
Dans la section suivante, nous allons nous intéresser à la Réalisation de cartes.
