7. Topología
Objetivos: |
Entender la topología en datos vectoriales |
|
Palabras clave: |
Vector, topología, normas de topología, errores de topología, radio de búsqueda, distancia de captura, características básicas |
7.1. Vista general
Topología expresa las relaciones espaciales entre características de vectores (puntos, polilíneas y polígonos) conectados o adyacentes en un SIG. Los datos topológico o basados en la topología sirven para detectar y corregir errores de digitalización (p.ej. dos líneas en una capa vectorial de vías que no se juntan perfectamente en una intersección). La topogía es necesaria para llevar a cabo algunos tipos de análisis espacial, como el análisis de red.
Imagina que viajas a Londres. En un recorrido turístico, planea visitar la Catedral de St. Paul primero y por la tarde el mercado de Covent Garden para comprar algunos recuerdos. Mirando el mapa del metro de Londres (ver Figura 7.2) tienes que encontrar trenes de conexión para ir de Covent Garden a St. Paul’s. Esto requiere información topológica (datos) sobre dónde es posible cambiar de tren. Al mirar un mapa del subsuelo, las relaciones topológicas se ilustran mediante círculos que muestran conectividad.
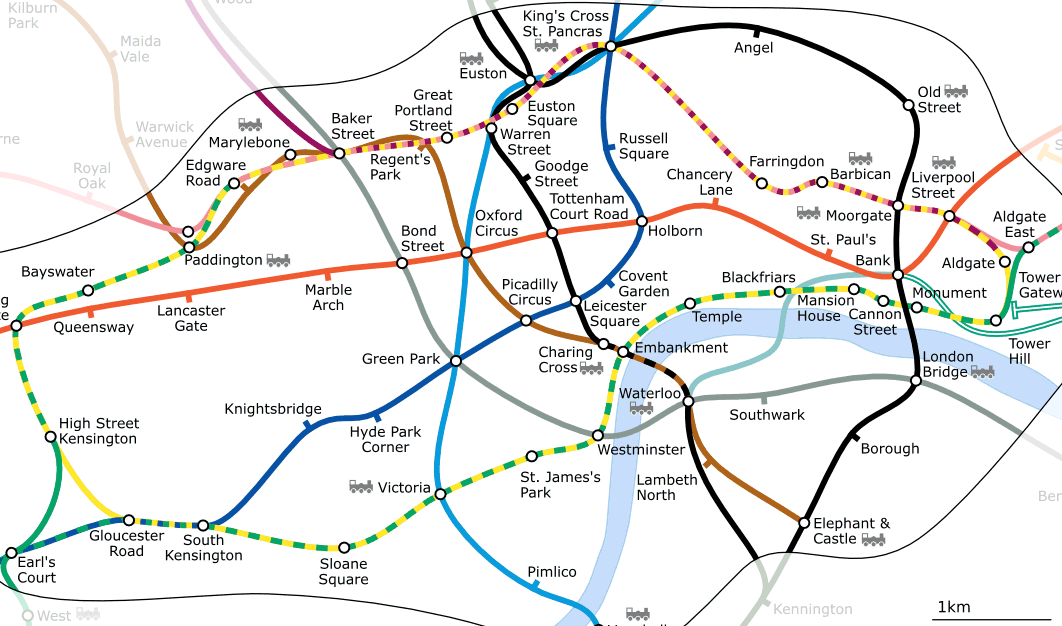
Figura 7.2 Topología de la red de Metro de Londres.
7.2. Errores de topología
Existen diferentes tipos de errores topológicos y se pueden agrupar según si los tipos de entidades vectoriales son polígonos o polilíneas. Los errores topológicos con entidades de polígono pueden incluir polígonos sin cerrar, espacios entre los bordes de los polígonos o bordes de polígonos superpuestos. Un error topológico común con las entidades de polilínea es que no se encuentran perfectamente en un punto (nodo). Este tipo de error se denomina subalcance si existe un espacio entre las líneas y sobrealcance si una línea termina más allá de la línea a la que debe conectarse (consulte Figura 7.3).
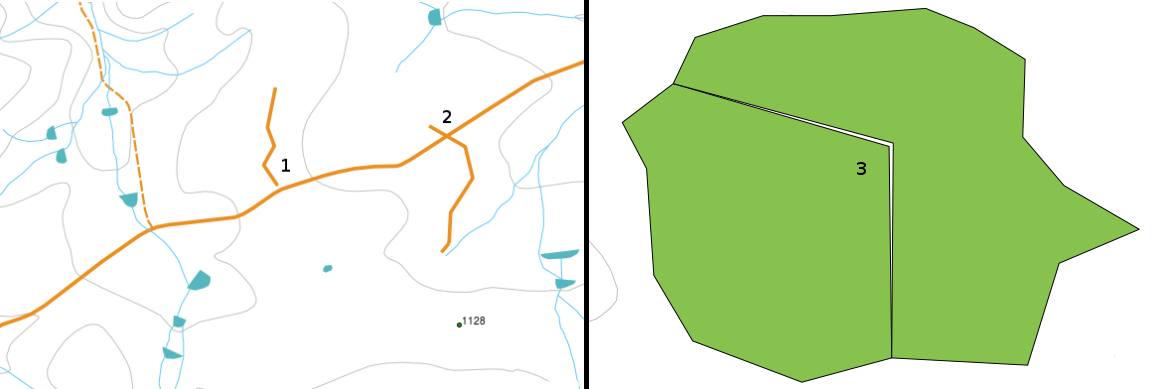
Figura 7.3 Undershoots (1) ocurren cuando las líneas vectoriales digitalizadas que deberían estar conectadas no llegan a estarlo. Overshoots (2) ocurren cuando una línea termina más allá de la línea con la que debería estar conectada. Slivers (3) ocurren cuando los vértices de dos polígonos no coinciden en los bordes.
El resultado de los errores de undershoot y overshoot se denomina «nodos colgados» al final de las líneas. Los nodos colgados son aceptables en casos especiales, por ejemplo si están adjuntos a una calle sin salida.
Los errores topológicos rompen la relación entre los elementos. Hay que solucionar estos errores para poder analizar los datos vectoriales con procedimientos como el análisis de red (p. ej. encontrar la mejor ruta por una red de carreteras) o medición (p. ej. descubrir la longitud de un río). La topología no solo es útil para el análisis de red y medición, hay además otras razones por las que es importante y útil crear o tener datos vectoriales con una topología correcta. Solo hay que imaginar digitalizar un mapa de límites municipales para una provincia y que los polígonos se superpongan o muestren astillas. Si esos errores existen, se podrían utilizar las herramientas de medición, pero los resultados serían incorrectos. No se consigue el área correcta de cualquier municipio ni definir exactamente dónde se encuentra el límite entre los municipios.
Crear y tener datos topológicos correctos no solo es importante para tu propio análisis sino también para la gente que reciba esos datos. ¡Esperan que esos datos y resultados de análisis sean correctos!
7.3. Normas de topología
Por suerte, muchos de los errores comunes que pueden ocurrir al digitalizar las características de vector pueden evitarse con las normas de topología que se implementan en muchas apliaciones SIG.
A excepción de algunos formatos de datos SIG, la topología no se suele aplicar por defecto. Muchos SIG, como QGIS, definen la topología como normas de relaciones y dejan al usuario elegir las normas, si las hay, para que se implementen en una capa vectorial.
La siguiente lista muestra algunos ejemplos de dónde se pueden definir algunas normas de topología para objetos del mundo real en un mapa vectorial:
Los bordes del área de un mapa municipal no deben superponerse.
Los bordes del área de un mapa municipal no deben tener espacios vacíos (astillas).
Los polígonos que muestren límites de propiedad deben estar cerrados. No se permiten los undershoot u overshoot en las líneas de los bordes.
Las líneas de contorno en una capa de línea vectorial no deben intersecarse (cruzar una a otra).
7.4. Herramientas de topología
Muchas aplicaciones GIS proporcionan herramientas para la edición topológica. Por ejemplo, en QGIS puede habilitar la edición topológica para mejorar la edición y mantener límites comunes en capas de polígonos. Un SIG como QGIS “detecta” un límite compartido en un mapa de polígono, por lo que solo tiene que mover el vértice del borde de un límite de polígono y QGIS garantizará la actualización de los otros límites de polígono como se muestra en Figura 7.4 (1).
Otra opción topológica le permite evitar superposiciones de polígonos durante la digitalización (consulte Figura 7.4 (2)). Si ya tiene un polígono, con esta opción es posible digitalizar un segundo polígono adyacente para que ambos polígonos se superpongan y QGIS luego recorte el segundo polígono al límite común.
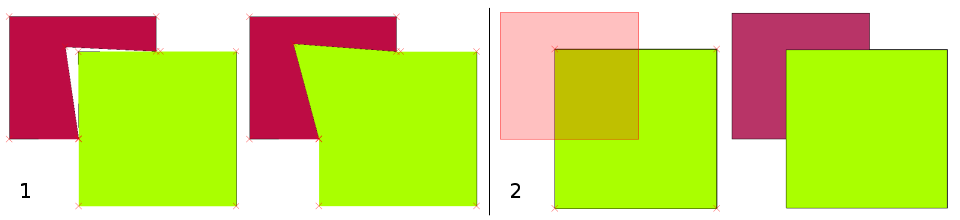
Figura 7.4 (1) Topological editing to detect shared boundaries, when moving vertices. When moving a vertex, all features that share that vertex are updated. (2) To avoid polygon overlaps, when a new polygon is digitised (shown in red) it is clipped to avoid overlapping neighbouring areas.
7.5. Distancia de captura
La distancia de ajuste es la distancia que usa un SIG para buscar el vértice y/o segmento más cercano que está tratando de conectar cuando digitaliza. Un segmento es una línea recta formada entre dos vértices en un polígono o geometría de polilínea. Si no se encuentra dentro de la distancia de ajuste, un SIG como QGIS dejará el vértice donde suelta el botón del mouse, en lugar de ajustarlo a un vértice y/o segmento existente (consulte Figura 7.5).
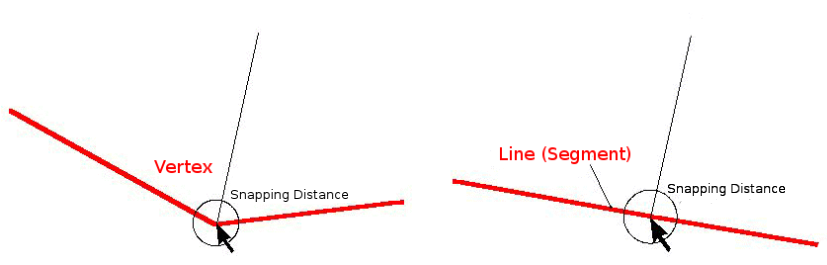
Figura 7.5 La distancia de captura (círculo negro) viene definida en unidades de mapa (p. ej. grados decimales) para capturar vértices o segmentos.
7.6. Radio de búsqueda
El radio de búsqueda es la distancia que un SIG utiliza para buscar el vértice más cercano que se esté intentando mover cuando se haga clic sobre el mapa. Si no estás en el radio de búsqueda, el SIG no encontrará ni seleccionará ningún vértice de un objeto para la edición. En principio es bastante parecido a la funcionalidad de la distancia de captura.
Tanto la distancia de captura como el radio de búsqueda vienen expresados en unidades de mapa, por lo que quizá tengas que experimentar para conseguir establecer el valor de distancia correcto. Si se especifica un valor demasiado alto, puede que el SIG capture el vértice erróneo, sobre todo si se trabaja con un gran número de vértices cercanos. Si se especifica el radio de búsqueda demasiado pequeño, la aplicación SIG no encontrará ningún objeto o vértice para mover o editar.
7.7. Problemas comunes/cosas a tener en cuenta
Diseñado principalmente para la simplicidad y la representación rápida, pero no para el análisis de datos que requiere topología (como encontrar rutas a través de una red), muchas aplicaciones SIG pueden mostrar datos topológicos y de entidades simples juntas y algunas también pueden crear, editar y analizar ambas.
7.8. ¿Qué hemos aprendido?
Vamos a resumir lo que hemos visto en esta hoja de ejercicios:
La topología muestra la relación espacial de las características de vector próximas.
Las herramientas topológicas proporcionan datos en SIG.
Se puede utilizar la topología para detectar y corregir errores de digitalización.
Para algunas herramientas como análisis de red, los datos topológicos son esenciales.
La distancia de captura y el radio de búsqueda nos ayudan a digitalizar datos vectoriales correctos de topología.
Los datos de objetos simples no es un formato de información topológica real pero se utiliza en las aplicaciones SIG.
7.9. ¡Ahora inténtalo!
Aquí están algunas ideas para probarlas con los alumnos:
Marca las paradas de autobús locales en un mapa topográfico y luego pide a los alumnos que encuentren la ruta más corta entre dos paradas.
Piensa en cómo crearías objetos vectoriales en un SIG para representar una red de carreteras topológica de tu ciudad. ¿Qué normas de topología son importantes y qué herramientas pueden utilizar los alumnos en un QGIS para asegurar que la nueva capa de la vía es topológicamente correcta?
7.10. Algo para pensar
En caso de no tener un ordenador disponible, siempre se puede utilizar un mapa de una red de autobuses o ferroviaria y analizar las relaciones espaciales y topolgía con los alumnos.
7.11. Otras lecturas
Libros:
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Páginas web:
La Guía de Usuario de QGIS contiene información más detallada sobre la edición topológica que proporciona QGIS.
7.12. ¿Qué sigue?
¡En la siguiente sección veremos más de cerca los Sistemas de Referencia de Coordenadas para entender cómo reflejamos los datos de nuestra Tierra esférica en mapas planos!
