重要
翻訳は あなたが参加できる コミュニティの取り組みです。このページは現在 100.00% 翻訳されています。
11. 空間分析(補間)
目的 |
空間分析の一環としての補間の理解 |
|
キーワード: |
ポイントデータ、補間法、逆距離加重補間、三角形分割補間 |
11.1. 概要
空間分析 は、元のデータから新しい情報と意味を抽出するために空間情報を操作する処理です。ふつうは空間分析は地理情報システム(GIS)を使用して実行されます。 GISにはたいてい、地物統計を計算し、データ補間のようなジオプロセッシング操作を実行するための空間分析ツールがあります。水文学では、ユーザーは地形解析と水文学モデリング(水の移動をモデル化すること)の重要性を強調するでしょう。野生生物管理の世界では、ユーザーは、野生生物の点位置およびそれらの環境との関係を扱う分析機能に関心があります。それぞれのユーザーは、自分が行っている仕事の種類に応じて、関心を持つものはさまざまに異なるでしょう。
11.2. 空間補間の詳細
空間補間は、既知の値を持つポイントを使用して、他の未知のポイントの値を推定する手順です。たとえば、自国の降水量(降雨量)地図を作成するために、地域全体をカバーするのに十分に均等に広がった気象観測所を見つけることはできません。空間補間では、近くの気象観測所での既知の温度測定値を使用して、データが記録されていない場所の温度を推定できます( 図 11.47 参照)。このタイプの内挿されたサーフェスは、多くの場合、 統計サーフェス と呼ばれます。標高データ、降水量、積雪量、地下水面、人口密度は、内挿を使用して計算できる他のタイプのデータです。
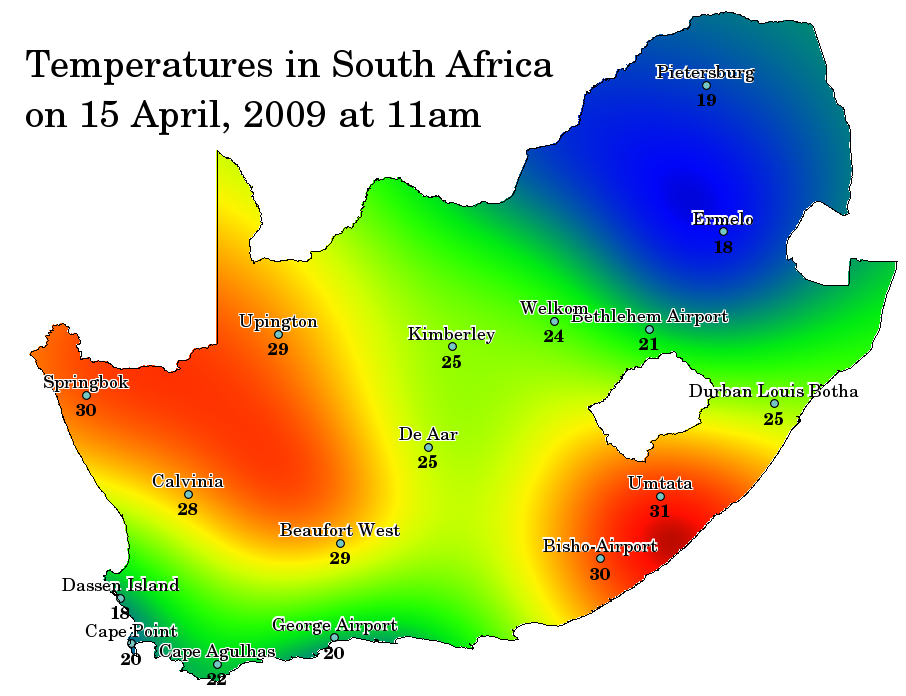
図 11.47 気温図は、南アフリカの気候条件から補間されています。
データ収集はコストが高く資源は限られているため、通常は選択されたポイント位置で限定された数だけ実施されます。 GISにおいて、これらの点に空間補間を適用すると、全てのラスタのセルに対して行われた推定値を持つラスタサーフェスを作成できます。
連続的な地図を、例えばGPS装置で計測された高度地点からのデジタル標高地図を生成するためには、適切な補間方法を使用して、サンプルまたは計測が行われなかった場所の値を最適に推定しなければなりません。補間解析の結果はその後、全領域をカバーする解析やモデリングに使用できます。
多くの補間方法があります。本稿では、逆距離加重 (IDW)と 不規則三角網 (TIN)と呼ばれる2つの広く使用される補間方法を紹介します。その他の補間方法をお探しの場合は、このトピックの末尾にある「さらに読む」セクションを参照してください。
11.3. 逆距離加重(IDW)
IDW内挿法では、サンプルポイントは内挿中に重み付けされ、作成する未知のポイントからの距離に応じて、あるポイントの別のポイントに対する影響が減少します( 図 11.48 参照)。

図 11.48 重み付けられたサンプル点の距離に基づく逆距離加重補間(左)。標高ベクタポイントからの補間IDWサーフェス(右)。画像元: Mitas, L., Mitasova, H. (1999).
重み付けが、新しい点からの距離が増加するにつれて重み付けの影響がどのように低下するかを制御する重み付け係数を使用して、サンプル点に割り当てられます。重み付け係数が大きくなるほど、補間処理に与える効果はその未知の点から遠い点ほど小さくなります。係数が増加するにつれ、未知の点の値は最も近い観測点の値に近づきます。
IDW内挿法には、いくつかの欠点もあることに注意することが重要です。サンプルデータポイントの分布が不均一な場合、内挿結果の品質が低下する可能性があります。さらに、内挿されたサーフェスの最大値と最小値は、サンプルデータポイントでのみ発生する可能性があります。これにより、 図 11.48 に示すように、サンプルデータポイントの周囲に小さなピークとピットが生じることがよくあります。
GISでは、内挿結果は通常2次元ラスタレイヤとして表示されます。 図 11.49 では、GPSデバイスを使用して野外で収集された標高サンプルポイントに基づいた、典型的なIDW補間結果を確認できます。
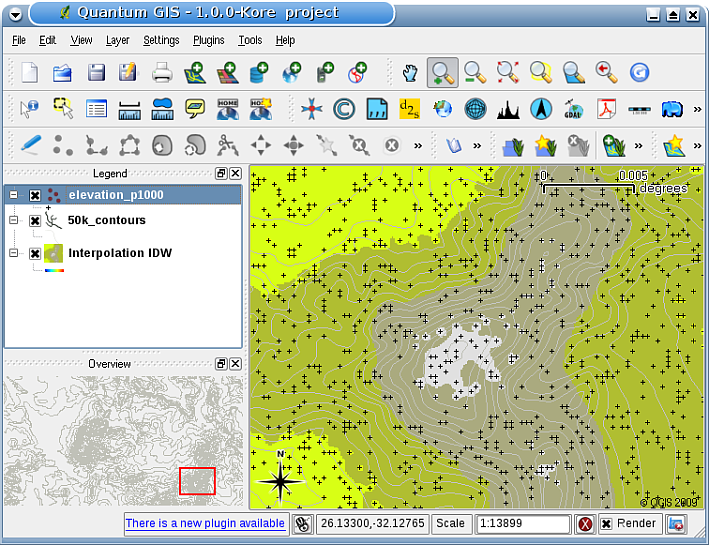
図 11.49 IDW補間では不規則に集められた標高サンプルポイント(黒十字で示す)から結果が得られます。
11.4. 不規則三角網(TIN)
TIN補間は、GISで人気のあるもう1つのツールです。一般的なTINアルゴリズムは、 ドロネー三角形分割 と呼ばれます。これは、最も近い隣接点の三角形によって形成されるサーフェスを作成しようとします。これを行うには、選択したサンプルポイントの周囲に外接円を作成し、それらの交点を重なり合わない、可能な限りコンパクトな三角形のネットワークに接続します( 図 11.50 参照)。
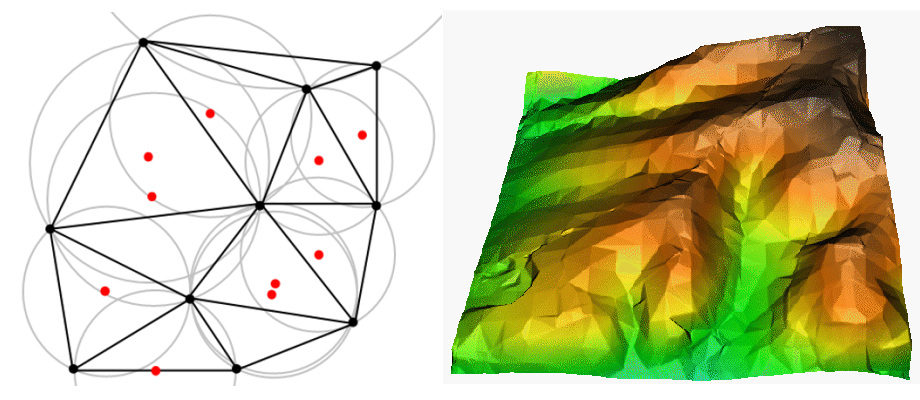
図 11.50 赤のサンプルデータの周りの外接円とのドロネー三角形分割。標高ベクタポイントから作成された結果として補間したTINサーフェスを右側に示します。画像元: Mitas, L., Mitasova, H. (1999).
TIN補間の主な欠点は、サーフェスが滑らかでなく、ギザギザの外観になる可能性があることです。これは、三角形のエッジとサンプルデータポイントでの不連続な勾配が原因で発生します。さらに、三角測量は通常、収集されたサンプルデータポイントのある領域を超えた外挿には適していません( 図 11.51 参照)。
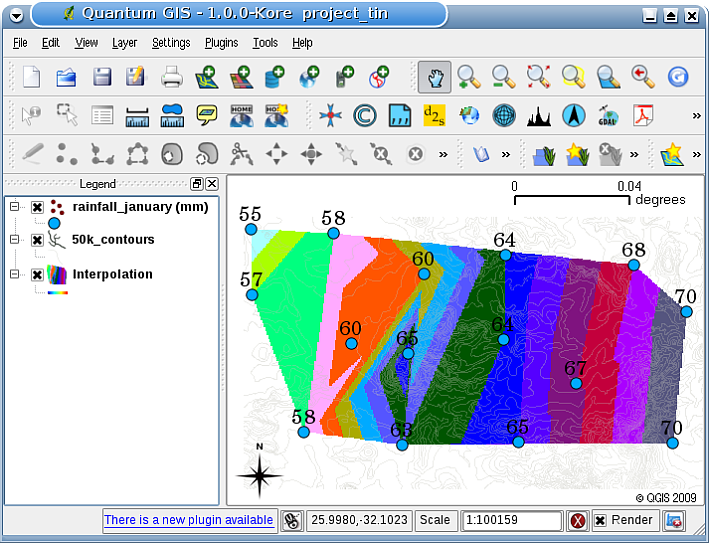
図 11.51 ドローネTIN補間は不規則に収集された降水量のサンプルポイント(青い円)に由来します。
11.5. 一般的な問題 / 注意すべき点
すべての状況に適用できる単一の補間方法はないことを覚えておくことが重要です。いくつかは他より正確で有用ですが、計算に時間がかかります。それらには長所と短所があります。実際には、どの補間方法を選択するかは、サンプルデータ、生成されるべき表面のタイプおよび推定誤差の許容誤差に応じて変えるべきです。一般的に、3つのステップの手順が推奨されます。
サンプルデータを評価します。これはデータが地域にどう分布しているかについてのアイデアを得るために行います。どの補間法を使用するかについてのヒントを提供するかもしれないので。
サンプルデータと研究目的の両方に最適な補間法を適用します。疑問がある場合には、利用可能であれば、複数の方法を試してみてください。
結果を比較し、最良の結果と最も適切な方法を見つけます。これは、最初は時間のかかるプロセスのように見えるかもしれません。しかし、さまざまな補間方法の経験と知識を得ると、最適なサーフェスを生成するために必要な時間が大幅に短縮されます。
11.6. その他の補間法
このワークシートではIDWおよびTIN補間法だけを取り上げましたが、GISには、張力付正規スプライン法(RST)、クリギングまたはトレンドサーフェス補間など、より多くの空間補間方法が用意されています。 Webリンクについては、以下の追加の読み物のセクションを参照してください。
11.7. わかりましたか?
ここでは以下のことを学びました:
補間 は 全領域をカバーするラスタサーフェスを作成することを目的とし未知の場所で値を推定するために、既知の値を持つベクターポイントを使用しています。
補間結果は通常は ラスタ レイヤです。
未知の場所の値を最適に推定する 適切な補間法を見つける ことが重要です。
IDW補間では、ある点から別の点への影響が推定される新点からの距離で減衰するように、サンプル点に重みを与えます。
TIN 補間 は最寄りのポイント情報に基づいた三角形で形成されたサーフェスを作成するためのサンプル点を使います。
11.8. やってみよう
ここでは人に教える際のアイデアいくつか述べていきます:
農業省があなたの地域で新しい耕作地を計画していますが、土壌の特性とは別に、収穫のために降雨量が十分あるかどうかを知りたいと考えています。利用可能なすべての情報は、周辺のいくつかの気象観測所から得られます。生徒たちといっしょに最高の降雨量がありそうな地域を示す補間サーフェスを作成してください。
観光局は、1月と2月に気象条件に関する情報を公開したいと考えています。彼らは気温、降雨量、風力データを持っており、気温や雨量、風の強さなどの気象条件が最適な場所を推測するためにデータを補間するよう求めます。これらの基準を満たす地域を特定できますか?
11.9. 考えてみよう
コンピュータを使用できない場合は、トポシートと定規を使用して架空の気象観測所間の等高線または降雨値の標高値を推定できます。たとえば、気象局Aの降雨量が 50 mmで、気象観測所Bの気温が 90 mmの場合、気象観測所AとBの真ん中での降雨量は 70 mmと推定できます。
11.10. 参考文献
図書:
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005): Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Mitas, L., Mitasova, H. (1999). Spatial Interpolation. In: P.Longley, M.F. Goodchild, D.J. Maguire, D.W.Rhind (Eds.), Geographical Information Systems: Principles, Techniques, Management and Applications, Wiley.
ウェブサイト:
QGISユーザーガイドには、QGISで提供される補間ツールの詳細な情報が含まれています。
11.11. 次は?
これは、このシリーズの最後のワークシートです。私たちは、QGISを探索し、GISソフトウェアで行うことができる他のすべてを発見するために、添付のQGIS説明書を使えるようになることをお勧めします!
