Importante
A tradução é um esforço comunitário você pode contribuir. Esta página está atualmente traduzida em 83.70%.
3. Dados Vectoriais
Objectivos: |
Compreender a utilização de modelos de dados vectoriais em ambiente SIG |
|
Palavras-chave: |
Vector, Ponto, Polilinha, Vértice, Geometria, Escala, Qualidade dos dados, Simbologia, Origem dos dados |
3.1. Resumo
Vector data provide a way to represent real world features within the GIS environment. A feature is anything you can see on the landscape. Imagine you are standing on the top of a hill. Looking down you can see houses, roads, trees, rivers, and so on (see Fig. 3.30). Each one of these things would be a feature when we represent them in a GIS Application. Vector features have attributes, which consist of text or numerical information that describe the features.

Fig. 3.30 Ao observar uma paisagem poderá identificar as suas entidades principais tais como: estradas, casas e árvores.
A vector feature has its shape represented using geometry. The geometry is
made up of one or more interconnected vertices. A vertex describes a position
in space using an X, Y and optionally Z axis. Geometries which have
vertices with a Z axis are often referred to as 2.5D since they describe
height or depth at each vertex, but not both.
When a feature’s geometry consists of only a single vertex, it is referred to as a point feature (see illustration Fig. 3.31). Where the geometry consists of two or more vertices and the first and last vertex are not equal, a polyline feature is formed (see illustration Fig. 3.32). Where three or more vertices are present, and the last vertex is equal to the first, an enclosed polygon feature is formed (see illustration Fig. 3.33).
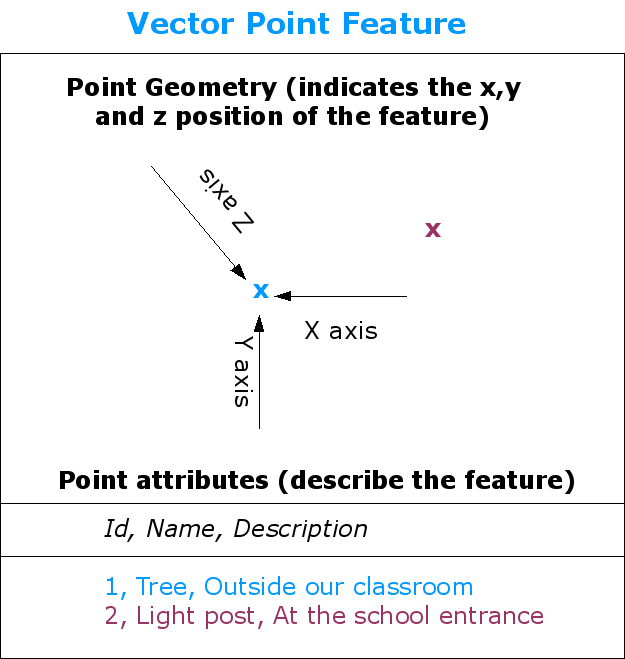
Fig. 3.31 Uma entidade ponto é descrita pelas suas coordenadas X, Y (e opcionalmente, Z) e pelos seus atributos. Estes últimos indicam-nos, p. ex., se o ponto se refere a uma árvore ou a um poste de iluminação pública.
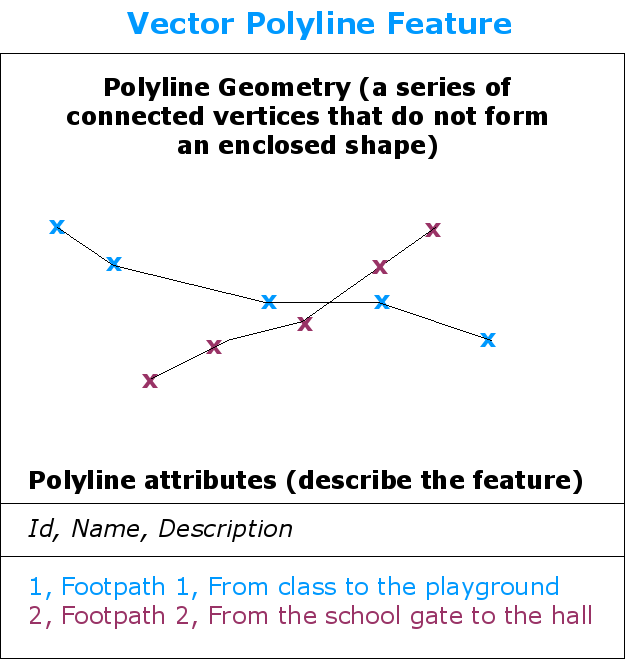
Fig. 3.32 Uma polilinha é uma sequência de vértices interligados. Cada vértice está definido pelas suas coordenadas X, Y (e opcionalmente, Z) e pelos seus atributos.
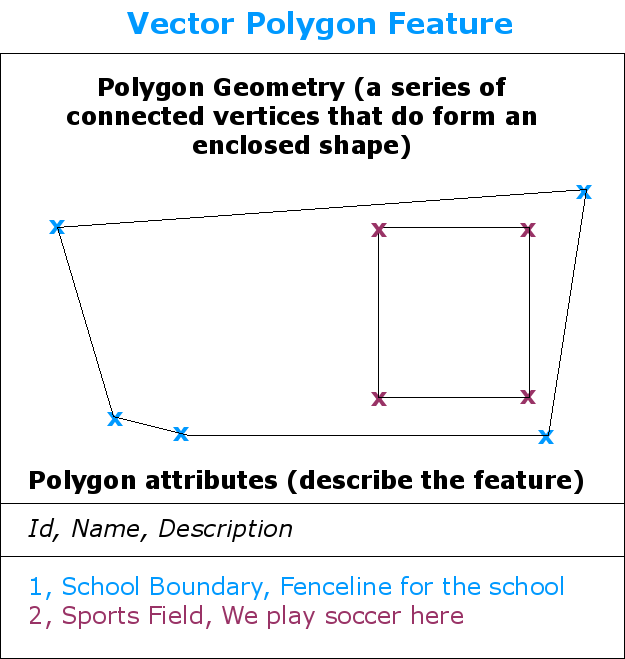
Fig. 3.33 Tal como uma polilinha, um polígono consiste numa sequência de vértices. Todavia, num polígono, o primeiro e último vértices ocupam sempre a mesma posição.
Looking back at the picture of a landscape we showed you further up, you should be able to see the different types of features in the way that a GIS represents them now (see illustration Fig. 3.34).
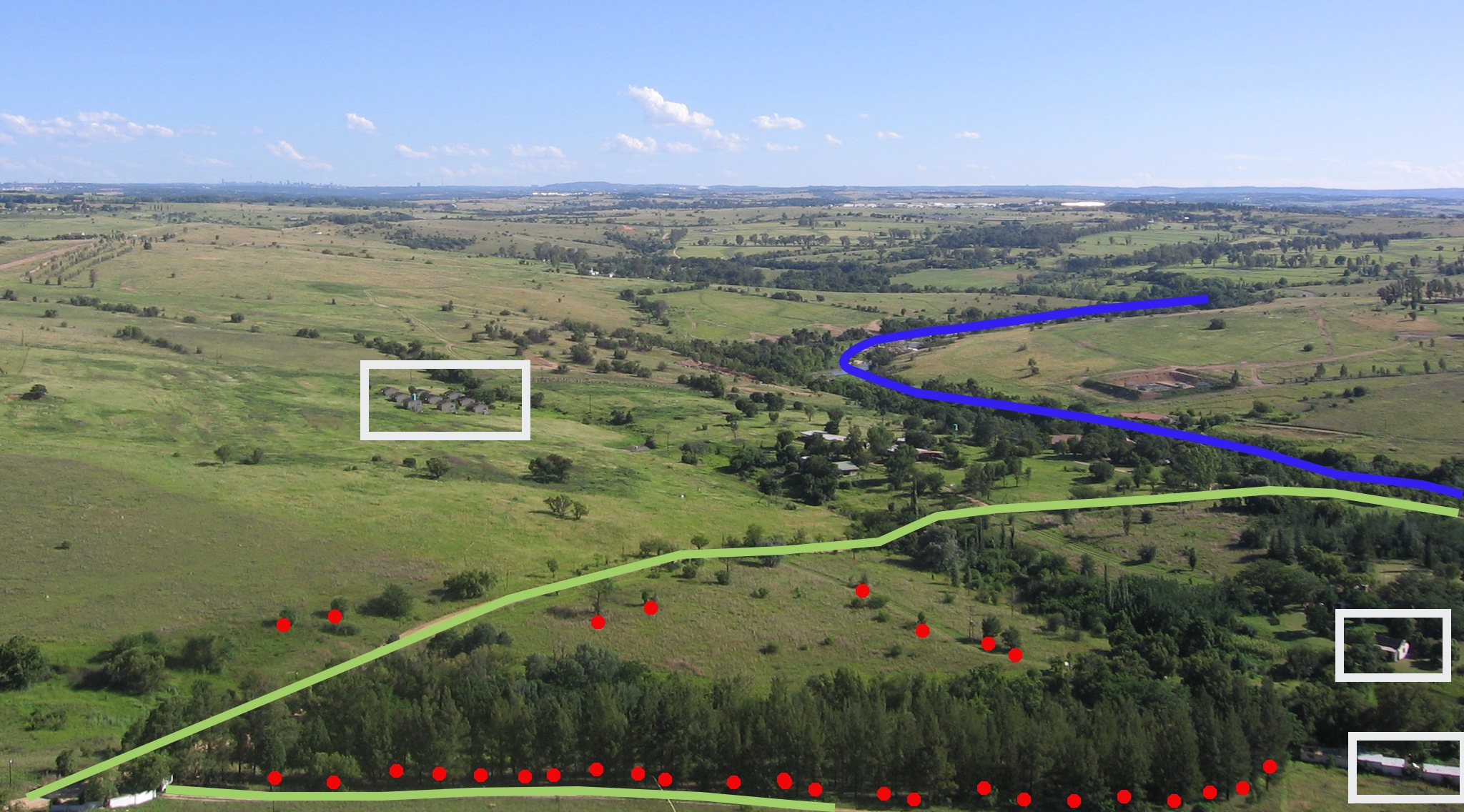
Fig. 3.34 Entidades da paisagem conforme representadas em ambiente SIG. Rios (a azul) e estradas (a verde) podem representar-se como linhas, árvores como pontos (a vermelho) e casas como polígonos (a branco).
3.2. Entidades Ponto - Detalhes
A primeira ideia a reter quando nos referimos a entidades ponto é a de que a descrição de um ponto num SIG é subjectiva e frequentemente dependente da escala. Tomemos o exemplo das cidades: se a escala do nosso mapa é pequena (grande área de cobertura), poderá fazer sentido representar uma cidade utilizando uma entidade ponto. Porém, se aumentarmos a escala de visualização, será mais adequado exibir a mesma cidade através de uma entidade polígono.
Escolher representar uma entidade como um ponto é principalmente uma questão de escala (de visualização adoptada pelo utilizador), de conveniência (as entidades ponto são mais fáceis e rápidas de criar que as entidades polígono) e do tipo de entidade a representar (não é razoável representar postes telefónicos como entidades do tipo polígono).
As we show in illustration Fig. 3.31, a point feature has an X, Y and optionally, Z value. The X and Y values will depend on the Coordinate Reference System (CRS) being used. We are going to go into more detail about Coordinate Reference Systems in a later tutorial. For now let’s simply say that a CRS is a way to accurately describe where a particular place is on the earth’s surface. One of the most common reference systems is Longitude and Latitude. Lines of Longitude run from the North Pole to the South Pole. Lines of Latitude run from the East to West. You can describe precisely where you are at any place on the earth by giving someone your Longitude (X) and Latitude (Y). If you make a similar measurement for a tree or a telephone pole and marked it on a map, you will have created a point feature.
Dado que a superfície terrestre não é plana mas rica em acidentes topográficos, torna-se muitas vezes útil adicionar uma coordenada Z à descrição da entidade ponto. Este valor é uma medida da altura desta entidade relativamente ao nível médio das águas do mar.
3.3. Entidades Polilinha - Detalhes
Where a point feature is a single vertex, a polyline has two or more vertices. The polyline is a continuous path drawn through each vertex, as shown in Fig. 3.32. When two vertices are joined, a line is created. When more than two are joined, they form a “line of lines”, or polyline.
A geometria de entidades lineares tais como estradas, rios, curvas de nível, caminhos pedonais, rotas aéreas, etc., é exibida através de polilinhas. A esta geometria básica torna-se por vezes necessário associar regras especiais. As curvas de nível, por exemplo, podem tocar-se (casos onde o terreno é escarpado) mas nunca cruzar-se. De maneira idêntica, as polilinhas utilizadas para armazenar uma rede de estradas devem estar ligadas nos respectivos cruzamentos e/ou entroncamentos. Em algumas aplicações SIG, estas regras podem definir-se de acordo com o tipo de entidade a representar (p.ex. estradas) e o sistema garantirá assim que essas polilinhas respeitem sempre essa definição.
If a curved polyline has very large distances between vertices, it may appear angular or jagged, depending on the scale at which it is viewed (see Fig. 3.35). Because of this it is important that polylines are digitised (captured into the computer) with distances between vertices that are small enough for the scale at which you want to use the data.
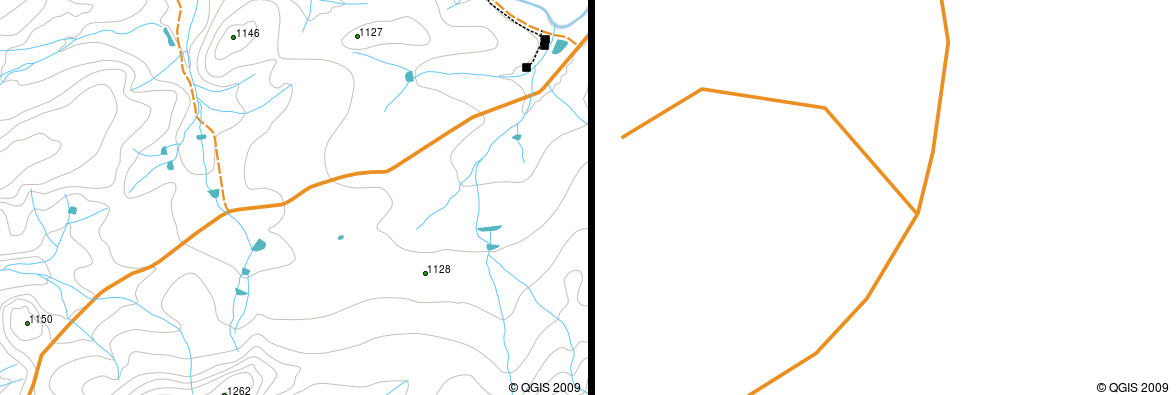
Fig. 3.35 Quando visualizadas a escalas pequenas (1:20 000, do lado esquerdo) as polilinhas podem aparentar um contorno curvilíneo suave. Quando visualizadas a escalas grandes (1:500, do lado direito) tomam frequentemente um aspecto segmentado anguloso.
The attributes of a polyline describe its properties or characteristics. For example a road polyline may have attributes that describe whether it is surfaced with gravel or tar, how many lanes it has, whether it is a one way street, and so on. The GIS can use these attributes to symbolise the polyline feature with a suitable colour or line style.
3.4. Entidades Polígono - Detalhes
As entidades polígono são áreas fechadas tais como barragens; ilhas, fronteiras de países, etc.. À semelhança das entidade polilinha, os polígonos criam-se à custa de vértices interligados por uma linha contínua. Todavia, uma vez que um polígono descreve sempre uma área fechada, os seus primeiro e último vértices devem sempre ocupar a mesma posição! Os polígonos possuem frequentemente geometria partilhada isto é, contornos ou fronteiras comuns a polígonos vizinhos. Muitas aplicações SIG tem a capacidade de assegurar automaticamente a coincidência entre contornos de polígonos contíguos. Um pouco mais à frente, no tópico Topologia veremos este assunto desenvolvido.
Da mesma forma que os pontos e as polilinhas, os polígonos também tem atributos. Os atributos descrevem cada polígono. Por exemplo, uma barragem pode ter atributos com informações sobre a profundidade e a qualidade da água.
3.5. Dados vectoriais - Camadas
Now that we have described what vector data is, let’s look at how vector data is managed and used in a GIS environment. Most GIS applications group vector features into layers. Features in a layer have the same geometry type (e.g. they will all be points) and the same kinds of attributes (e.g. information about what species a tree is for a trees layer). For example if you have recorded the positions of all the footpaths in your school, they will usually be stored together on the computer hard disk and shown in the GIS as a single layer. This is convenient because it allows you to hide or show all of the features for that layer in your GIS application with a single mouse click.
3.6. Dados Vectoriais - Edição
Uma aplicação SIG permite criar e modificar os dados das geometrias presentes numa camada através de um processo designado digitalização de que falaremos com mais detalhe num tutorial avançado. Se uma dada camada contêm polígonos (p. ex. charcos de água), a aplicação SIG permitirá aí a criação de apenas outros polígonos. De maneira idêntica, se se desejar modificar a forma de uma entidade, a aplicação só o permitirá na medida em que a forma resultante seja a correcta. Exemplificando: a aplicação não permitirá editar uma linha de tal forma que o resultado seja apenas um vértice (relembrar, na discussão anterior sobre linhas, o facto de todas estas terem obrigatoriamente pelo menos dois vértices)
A criação e edição de dados vectoriais são funções importantes de um SIG uma vez que constituem uma das principais formas de associarmos dados personalizados às entidades que nos interessa caracterizar. Digamos que estamos interessados em monitorizar poluentes num rio. Podemos utilizar o SIG para digitalizar ou vectorizar (como entidades ponto) todos os emissários de redes de drenagem pluvial encontrados ao longo do seu curso. Podemos inclusivamente vectorizar o rio (como uma entidade polilinha) e finalmente associar leituras dos níveis de pH, aos locais onde foram realizadas (vectorizando esses locais numa camada de entidades ponto).
Além de toda a informação que podemos criar, existem também muitos dados vectoriais de utilização livre e gratuita. Podemos p. ex. obter dados vectoriais das folhas da carta 1:50 000 do Instituto Cartográfico Nacional Sul-Africano.
3.7. Dados Vectoriais e Escala
Map scale is an important issue to consider when working with vector data in a GIS. When data is captured, it is usually digitised from existing maps, or by taking information from surveyor records and global positioning system devices. Maps have different scales, so if you import vector data from a map into a GIS environment (for example by digitising paper maps), the digital vector data will have the same scale issues as the original map. This effect can be seen in illustrations Fig. 3.36 and Fig. 3.37. Many issues can arise from making a poor choice of map scale. For example using the vector data in illustration Fig. 3.36 to plan a wetland conservation area could result in important parts of the wetland being left out of the reserve! On the other hand if you are trying to create a regional map, using data captured at 1:1000 000 might be just fine and will save you a lot of time and effort capturing the data.
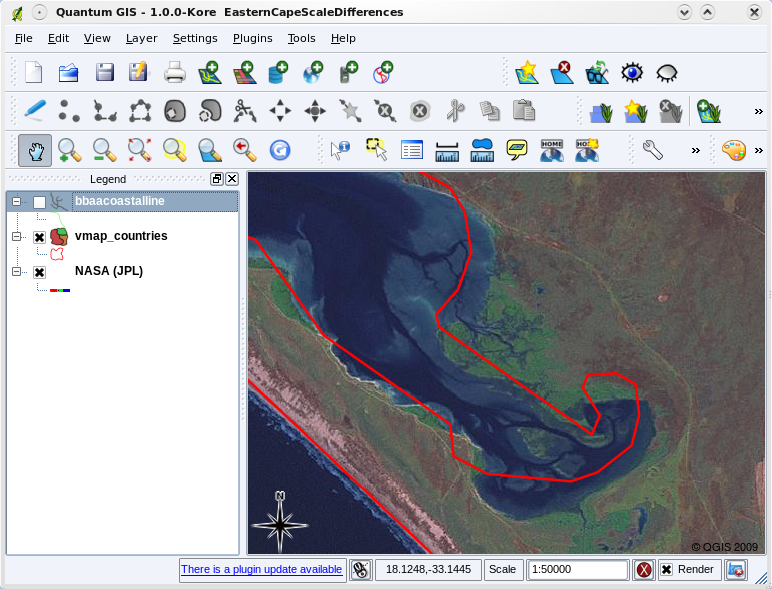
Fig. 3.36 Dados vectoriais (linhas vermelhas) digitalizados a partir de uma carta de pequena escala (1:1 000 000).
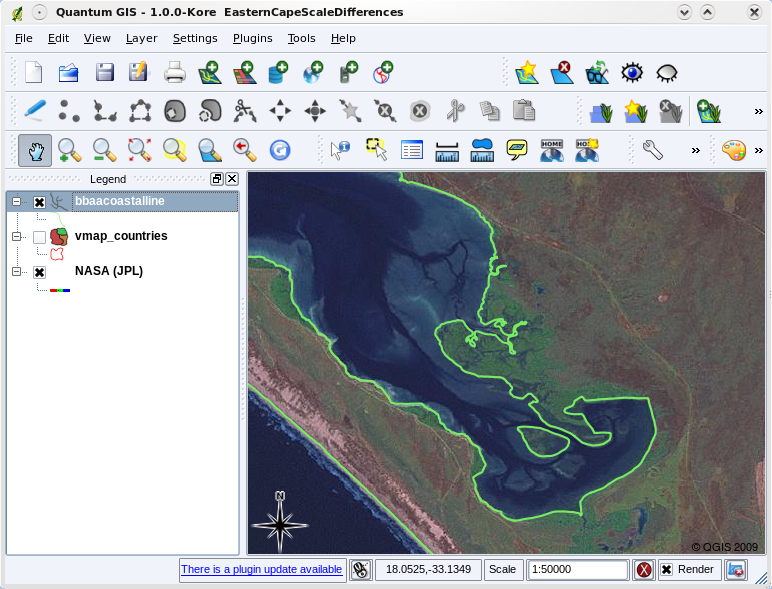
Fig. 3.37 Dados vectoriais (linhas verdes) digitalizados a partir de um mapa de grande escala (1:50 000).
3.8. Simbologia
When you add vector layers to the map view in a GIS application, they will be drawn with random colours and basic symbols. One of the great advantages of using a GIS is that you can create personalised maps very easily. The GIS program will let you choose colours to suite the feature type (e.g. you can tell it to draw a water bodies vector layer in blue). The GIS will also let you adjust the symbol used. So if you have a trees point layer, you can show each tree position with a small picture of a tree, rather than the basic circle marker that the GIS uses when you first load the layer (see illustrations Fig. 3.38, Fig. 3.39 and Fig. 3.40).
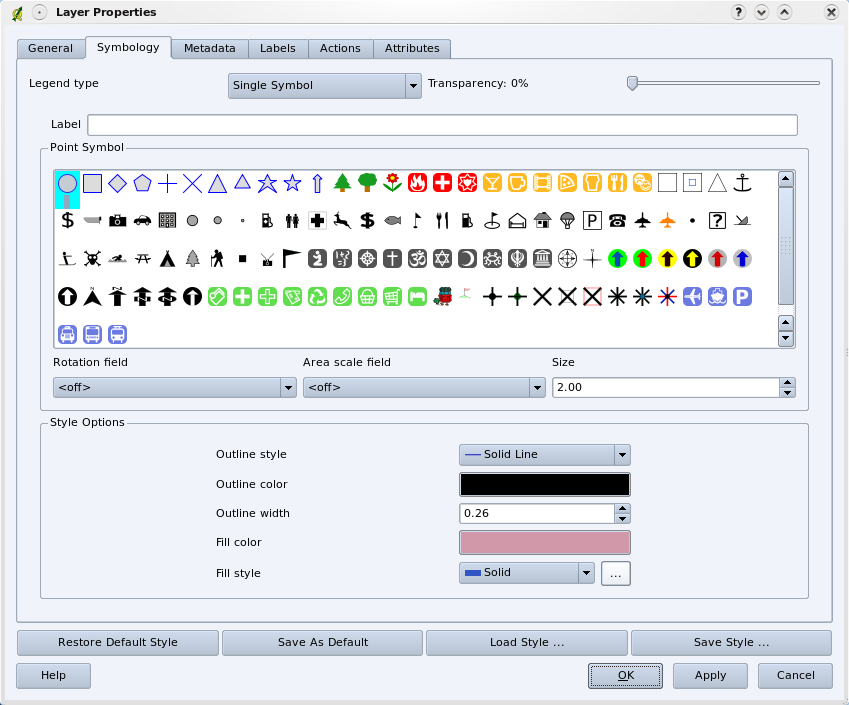
Fig. 3.38 Em ambiente SIG podemos utilizar um painel (como o apresentado em cima) para definir a forma como as entidades de uma camada devem ser exibidas.
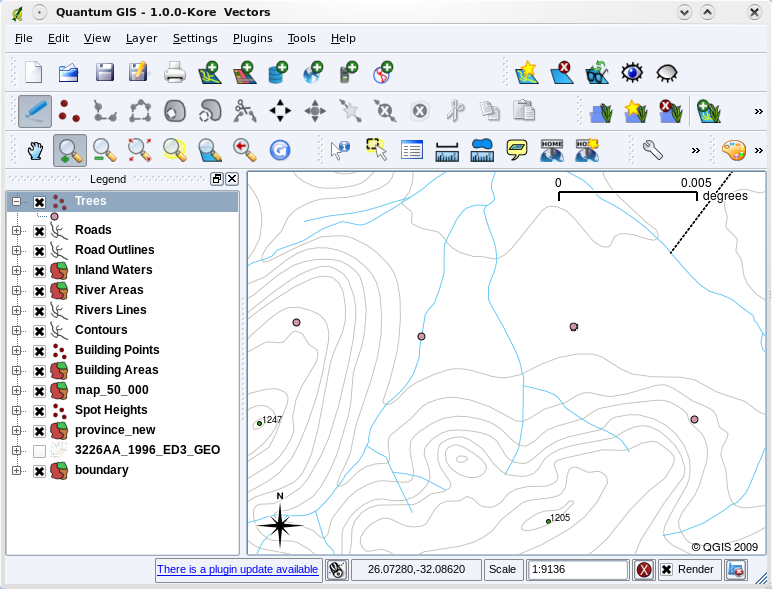
Fig. 3.39 Quando uma camada (p. ex. a camada de árvores acima) é carregada no SIG pela primeira vez, esta aplicação atribui-lhe um símbolo genérico.
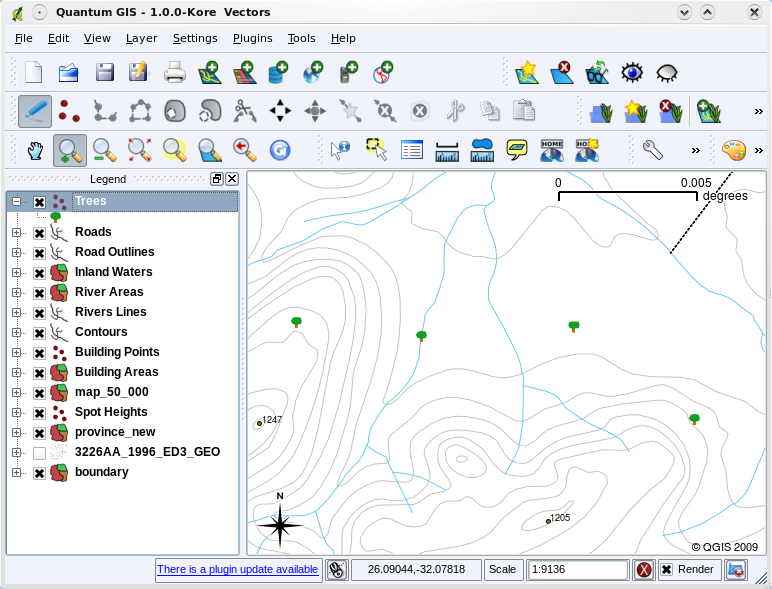
Fig. 3.40 Depois de fazermos alguns ajustamentos torna-se mais fácil de perceber que os nossos pontos representam árvores.
A simbologia é uma característica poderosa de um SIG, tornando os mapas mais apelativos e os dados mais fáceis de interpretar. No tópico que se segue (Atributos dos dados vetoriais) iremos explorar em maior profundidade o modo como a simbologia pode auxiliar um utilizador a compreender dados vectoriais.
3.9. Num SIG, que é possível fazermos com dados vectoriais?
Em termos simples, numa aplicação SIG, podemos utilizar dados vectoriais da mesma maneira que utilizaríamos os dados analógicos de um mapa topográfico. O verdadeiro poder do SIG começa a revelar-se quando se colocam questões tais como: «Quantas casas se encontram abrangidas pelo leito de inundação da “cheia centenária” de um rio?» ou «Qual o melhor local para se construir um hospital garantindo a acessibilidade do maior número possível de utentes?». Ou ainda: «Quantos alunos vivem num dado bairro?». Um SIG, apoiado na utilização de dados vectoriais, torna-se uma excelente ferramenta para responder a este tipo de questões. Geralmente, este processo de resposta designa-se por análise espacial. Nalguns tópicos mais adiante este assunto será abordado com maior detalhe.
3.10. Dados vectoriais - Problemas comuns
Trabalhar com dados vectoriais acarreta alguns problemas. Já mencionámos as questões que se podem levantar com vectores obtidos em diferentes escalas. A precisão e fiabilidade desses dados só se garantem à custa de trabalho e manutenção. Os dados vectoriais podem sofrer imprecisões quando os aparelhos utilizados na sua recolha não são devidamente operados ou calibrados ou quando os recursos empregues (prazos ou orçamentos) não permitem desenvolver o processo de recolha com o rigor suficiente.
If you have poor quality vector data, you can often detect this when viewing the data in a GIS. For example slivers can occur when the edges of two polygon areas don’t meet properly (see Fig. 3.41).
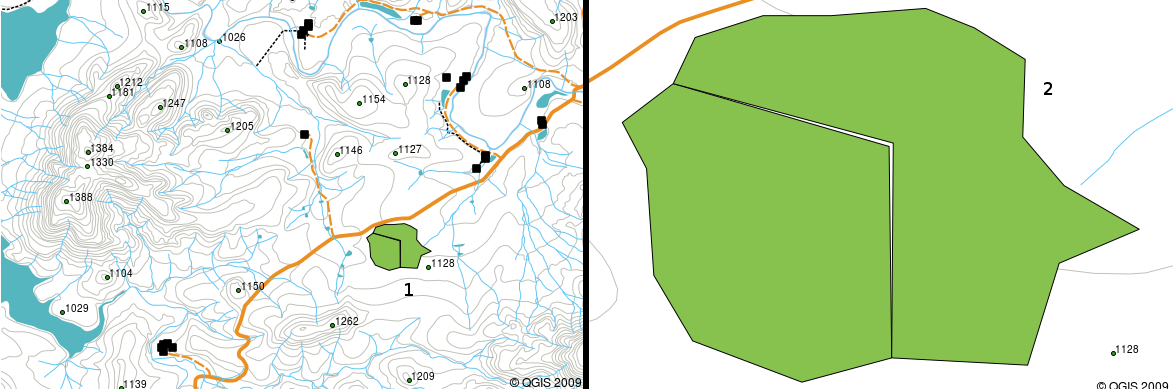
Fig. 3.41 As frestas ocorrem quando os vértices de dois polígonos não se encontram sobre as suas fronteiras. A uma escala pequena (p. ex. 1, do lado esquerdo) talvez não se consigam distinguir esses erros. Numa escala grande porém, eles aparecem como faixas estreitas compreendidas entre cada polígono (2, do lado direito).
Overshoots can occur when a line feature such as a road does not meet another road exactly at an intersection. Undershoots can occur when a line feature (e.g. a river) does not exactly meet another feature to which it should be connected. Figure Fig. 3.42 demonstrates what undershoots and overshoots look like.
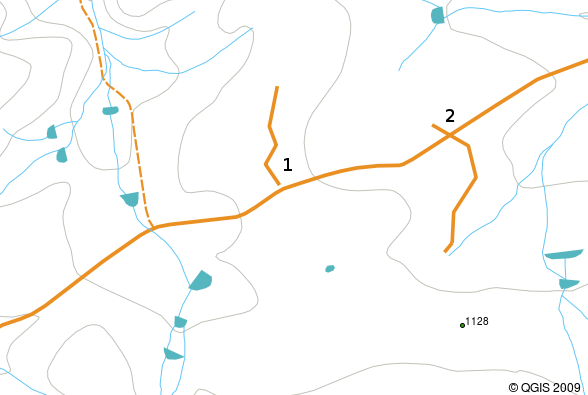
Fig. 3.42 A suspensão (1) ocorre quando linhas vectorizadas que deviam ligar-se uma à outra não entram efectivamente em contacto. A transposição (2) ocorre quando uma linha termina para além da outra à qual se deveria ligar.
Em face do erros que podem ocorrer, é muito importante vectorizar os dados de forma cuidadosa e precisa. No próximo tópico, Topologia, examinaremos alguns destes erros ao pormenor.
3.11. O que aprendemos?
Resumindo o que abordámos na lista seguinte:
Num SIG, os dados vectoriais são utilizados para representar elementos do mundo real (a essa representação chamámos entidade).
Uma entidade vectorial pode ter um geometria do tipo ponto, linha/polilinha ou polígono.
Cada entidade vectorial possuí atributos alfanuméricos que a descrevem.
A geometria das entidades é descrita à custa de vértices.
A geometria do ponto constitui-se de um vértice único (de coordenadas X, Y e opcionalmente Z).
A geometria da polilinha constitui-se de dois ou mais vértices interligados por uma linha.
A geometria do polígono constitui-se de pelo menos quatro vértices que dão forma a uma área fechada. A posição do primeiro e último vértices tem obrigatoriamente de coincidir.
A escolha do tipo de geometria a utilizar depende da escala de visualização, da conveniência e do fim a que se destinam os dados que armazenamos no SIG.
A maioria das aplicações SIG não permite combinar geometrias de diferentes tipos numa mesma camada.
A vectorização é o processo de delinear, numa aplicação SIG, dados vectoriais. [Os dados vectoriais resultam da representação digital (por oposição a analógica) de elementos do mundo real.]
Os dados vectoriais podem ver a sua qualidade afectada por erros aos quais precisamos de estar atentos: suspensões, transposições e frestas.
Numa aplicação SIG, os dados vectoriais podem ser utilizados em análise espacial para, por exemplo, encontrar o hospital mais próximo de uma determinada escola.
We have summarised the GIS Vector Data concept in Figure Fig. 3.43.
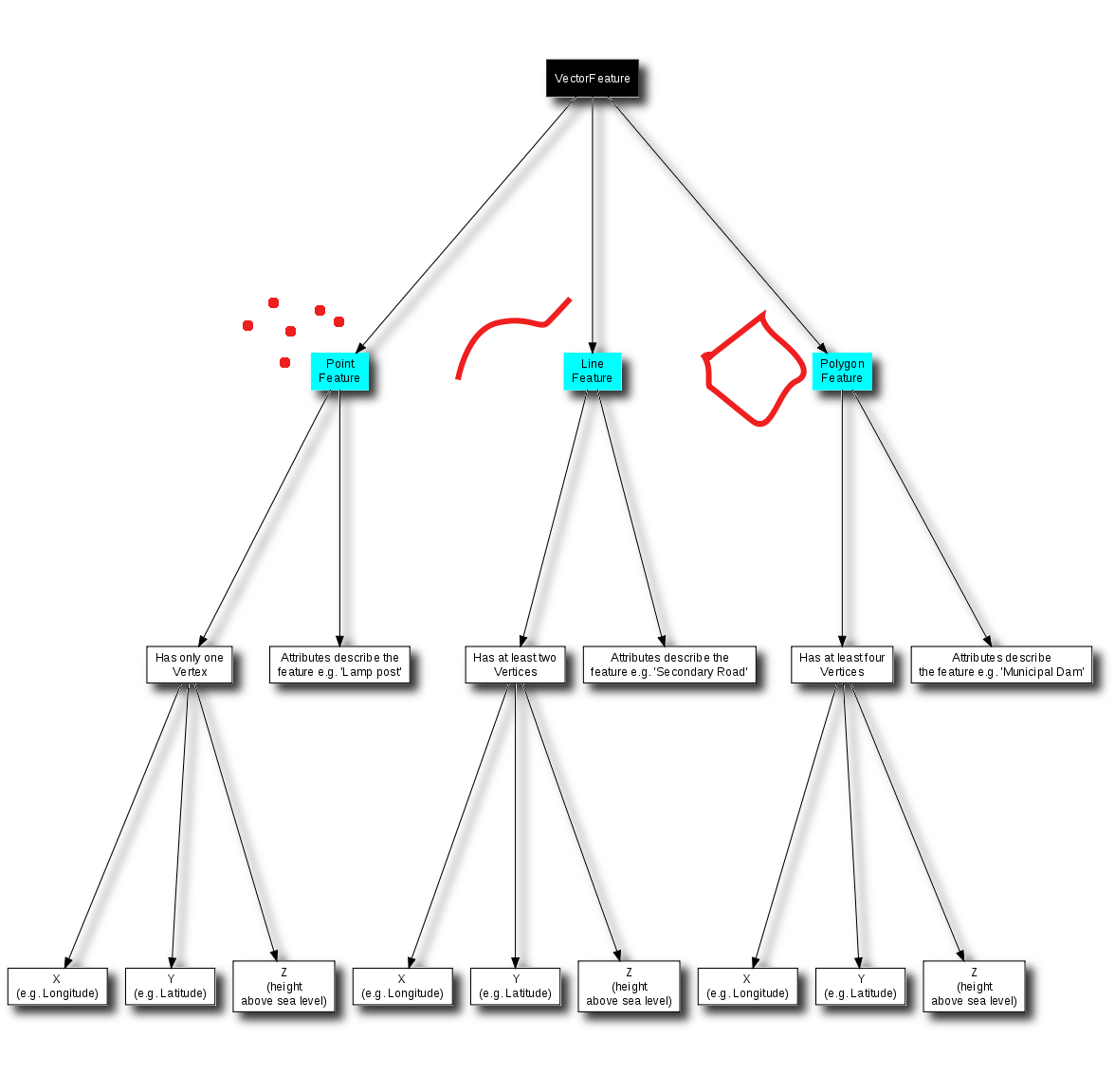
Fig. 3.43 Este diagrama mostra como as aplicações SIG lidam com os dados vectoriais.
3.12. Agora experimente!
Aqui está algumas ideias para experimentar com os seu alunos:
Using a copy of a toposheet map for your local area (like the one shown in Fig. 3.44), see if your learners can identify examples of the different types of vector data by highlighting them on the map.
Pensem na forma de criar num SIG, entidades vectoriais que representem elementos do mundo real presentes nos terrenos da vossa escola. Elaborem uma tabela com esses elementos e atribuam aos alunos a tarefa de decidir qual a tipo de entidade que melhor se adequa à sua representação: ponto, linha/polilinha ou polígono. Ver como exemplo a tabela table_vector_1.
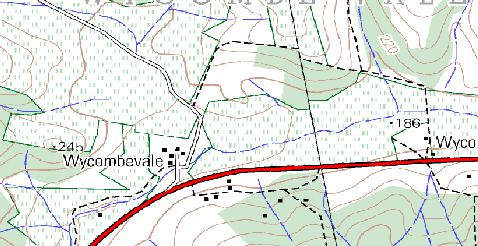
Fig. 3.44 Consegue identificar duas entidades ponto e uma entidade polígono neste mapa?
Entidade do mundo real |
Tipo de geometria adequado |
|---|---|
Mastro da bandeira da escola |
|
Campo de futebol |
|
Percursos pedonais dentro e ao redor da escola. |
|
Localização dos bebedouros |
|
Etc. |
Tabela Vectorial 1: Crie uma tabela como esta (sem preencher a coluna relativa ao tipo de geometria) e peça aos alunos que escolham o tipo de geometria mais adequado.
3.13. Algo para reflectir
Se não tem computador disponível, pode usar um mapa topográfico e uma folha de acetato (ou outra transparência) para ilustrar o conceito de dados vectoriais.
3.14. Outras leituras
O Guia do Utilizador QGIS contêm informação mais detalhada sobre manipulação de dados vectoriais.
3.15. O que vem a seguir?
Na secção que se segue lançaremos um olhar mais atento aos dados dos atributos para ver como podem ser utilizados na descrição das entidades vectoriais.
