Importante
La traducción es un esfuerzo comunitario puede unirse. Esta página está actualmente traducida en |progreso de traducción|.
11. Análisis Espacial (Interpolación)
Objetivos: |
Entender la interpolación como parte del análisis espacial |
|
Palabras clave: |
Datos de punto, método de interpolación, Distancia Inversa Ponderada, Red Irregular Triangulada |
11.1. Vista general
Análisis espacial es el proceso de manipular información espacial para extraer información nueva y significativa a partir de los datos originales. Usualmente el análisis espacial se realiza con un Sistema de Información Geográfica (SIG). Un SIG normalmente proporciona herramientas de análisis espacial para calcular estadísticas de las entidades y realizar actividades de geoprocesamiento como la interpolación de datos. En hidrología es posible que los usuarios enfaticen la importancia del análisis del terreno y del modelado hidrológico (modelar el movimiento del agua por sobre y dentro de la tierra). En la gestión de la vida salvaje, los usuarios están interesados en funciones analíticas que tratan con las ubicaciones de puntos de la vida salvaje y sus relaciones con el medio ambiente. Cada usuario tendrá diferentes cosas en las que está interesado dependiendo de la clase de trabajo que realicen.
11.2. Interpolación espacial en detalle
La interpolación espacial es el proceso de utilizar puntos con valores conocidos para estimar valores en otros puntos desconocidos. Por ejemplo, para hacer un mapa de precipitaciones (precipitaciones) para su país, no encontrará suficientes estaciones meteorológicas distribuidas uniformemente para cubrir toda la región. La interpolación espacial puede estimar las temperaturas en lugares sin datos registrados mediante el uso de lecturas de temperatura conocidas en estaciones meteorológicas cercanas (consulte Figura 11.38). Este tipo de superficie interpolada a menudo se denomina superficie estadística. Los datos de elevación, precipitación, acumulación de nieve, nivel freático y densidad de población son otros tipos de datos que se pueden calcular mediante interpolación.
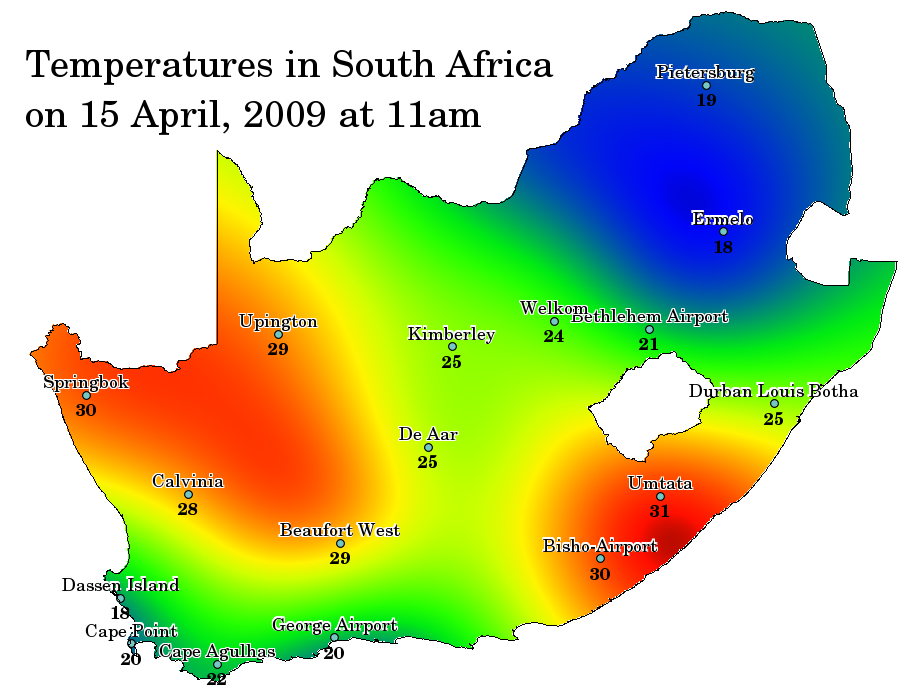
Figura 11.38 Mapa de temperaturas interpolado de estaciones meteorológicas Sudafricanas.
Debido al alto costo y a los recursos limitados la recolección de los datos usualmente es llevada a cabo sólo en un número limitado de ubicaciones de puntos seleccionados. En un SIG, la interpolación de esos puntos puede ser aplicada para crear una superficie ráster con estimaciones realizadas para todas las celdas del ráster.
Con el fin de generar un mapa continuo, por ejemplo, un mapa de elevaciones digitales de los puntos de elevación medidos con un dispositivo GPS, se debe utilizar un método de interpolación adecuado para estimar de manera óptima los valores en aquellas ubicaciones en donde no fueron tomadas muestras o mediciones. Los resultados del análisis de interpolación pueden entonces ser utilizados para análisis que cubran el área completa y para el modelado.
Existen muchos métodos de interpolación. En esta introducción se presentarán dos métodos de interpolación ampliamente usados llamados Distancia Inversa Ponderada (IDW por sus siglas en inglés) y Redes Irregulares Trianguladas (TIN por sus siglas en inlgés). Si se requieren métodos adicionales de interpolación, favor de referirse a la sección “Otras Lecturas” al final de este tema.
11.3. Distancia Inversa Ponderada (IDW)
En el método de interpolación IDW, los puntos de muestra se ponderan durante la interpolación de modo que la influencia de un punto en relación con otro disminuye con la distancia desde el punto desconocido que desea crear (consulte Figura 11.39).
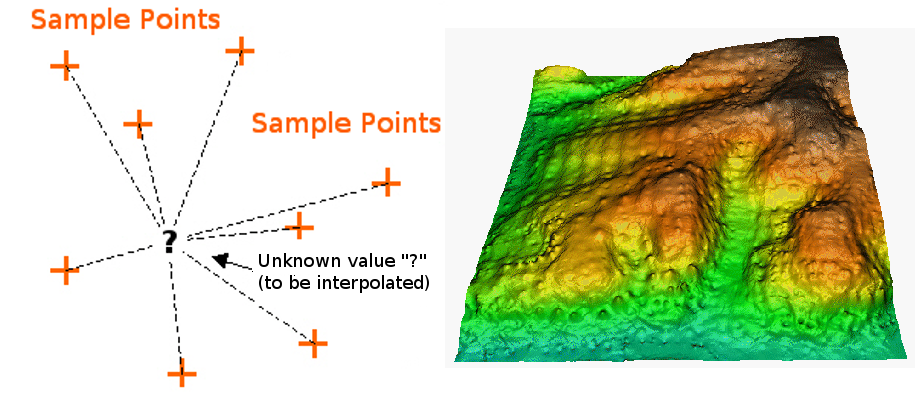
Figura 11.39 Interpolación Distancia Inversa Ponderada basada en la distancia del punto de muestra ponderada (izquierda). Superficie IDW interpolada de puntos vectoriales de elevación(derecha). Fuente de la Imagen: Mitas, L., Mitasova, H. (1999).
La ponderación es asignada a los puntos de muestreo mediante la utilización de un coeficiente de ponderación que controla cómo la influencia de la ponderación decae mientras la distancia hacia el punto nuevo se incrementa. Mientras más grande sea el coeficiente de ponderación menor será el efecto que los puntos tendrán si están lejos del punto desconocido durante el proceso de interpolación. Conforme el coeficiente se incrementa, el valor de los puntos desconocidos se aproxima al valor del punto de observación más cercano.
Es importante notar que el método de interpolación IDW también tiene algunas desventajas: la calidad del resultado de la interpolación puede disminuir si la distribución de los puntos de datos de la muestra es desigual. Además, los valores máximo y mínimo en la superficie interpolada solo pueden ocurrir en puntos de datos de muestra. Esto a menudo da como resultado pequeños picos y hoyos alrededor de los puntos de datos de muestra, como se muestra en Figura 11.39.
En SIG, los resultados de la interpolación generalmente se muestran como una capa ráster bidimensional. En Figura 11.40, puede ver un resultado de interpolación IDW típico, basado en puntos de muestra de elevación recolectados en el campo con un dispositivo GPS.
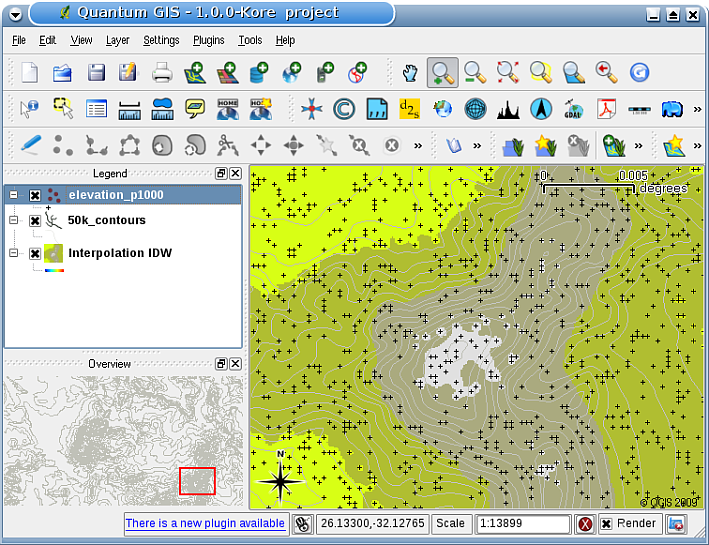
Figura 11.40 Resultado de la interpolación IDW a partir de puntos de muestra de elevación recolectados irregularmente (mostrados como cruces negras).
11.4. Red Irregular Triangulada (TIN)
La interpolación TIN es otra herramienta popular en SIG. Un algoritmo TIN común se llama triangulación de Delaunay. Intenta crear una superficie formada por triángulos de puntos vecinos más cercanos. Para hacer esto, se crean círculos circunferenciales alrededor de los puntos de muestra seleccionados y sus intersecciones se conectan a una red de triángulos no superpuestos y lo más compacta posible (ver Figura 11.41).
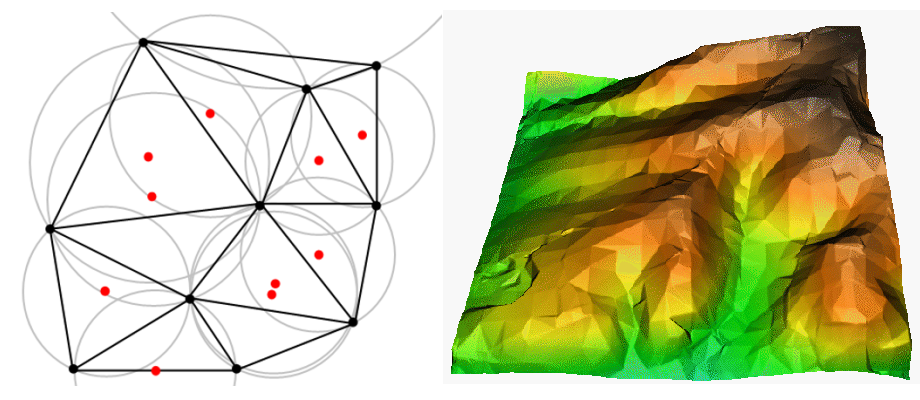
Figura 11.41 Triangulación de Delaunay con circunferencias alrededor de los datos de muestra rojos. La superficie TIN interpolada resultante creada a partir de puntos de vector de elevación se muestra a la derecha. Fuente de la imagen : Mitas , L., Mitasova , H. (1999).
La principal desventaja de la interpolación TIN es que las superficies no son lisas y pueden dar una apariencia irregular. Esto es causado por pendientes discontinuas en los bordes de los triángulos y puntos de datos de muestra. Además, la triangulación generalmente no es adecuada para la extrapolación más allá del área con puntos de datos de muestra recolectados (ver Figura 11.42 ).
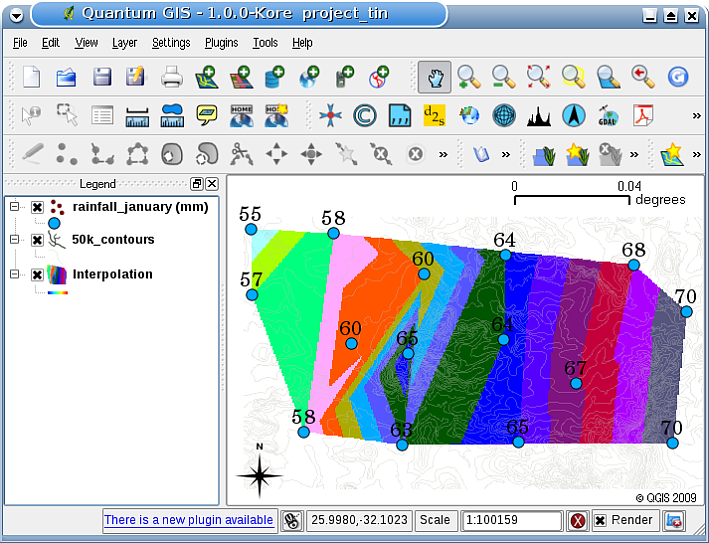
Figura 11.42 Interpolación TIN Delaunay resultado de puntos de muestra de lluvia recolectados irregularmente (círculos azules)
11.5. Problemas comunes / Cosas a tener en cuenta
Es importante recordar que no existe un solo método de interpolación que pueda ser aplicado a todas las situaciones. Algunos son más exactos y útiles que otros pero toman más tiempo en calcularse. Todos tienen ventajas y desventajas. En la práctica, la selección de un método de interpolación particular debería depender en los datos de muestra, el tipo de superficies a ser generadas y la tolerancia de errores estimados. Generalmente se recomienda un procedimiento de tres pasos:
Evaluar los datos de muestra. Realice esto para obtener una idea de cómo se distribuyen los datos en el área, ya que esto puede proporcionar pistas acerca de cual método de interpolación utilizar.
Aplicar un método de interpolación que más adecuado tanto para los datos de muestra como para los objetivos del estudio. cuando se tengan dudas, intentar varios métodos, si están disponibles.
Comparar los resultados y encontrar el mejor de ellos y el método más adecuado. Esto puede parecer como un proceso que consume mucho tiempo. Sin embargo, conforme se tenga más experiencia y conocimiento de los diferentes métodos de interpolación, el tiempo requerido para generar la superficie más adecuada se reducirá considerablemente.
11.6. Otros métodos de interpolación
Aunque en esta hoja de ejercicios nos concentramos en los métodos de interpolación IDW y TIN, existen métodos de interpolación espacial disponibles en los SIG, tales como los Splines con Tensión Regularizados (RST por sus siglas en inglés), Kriging o Interpolación de superficies con Tendencias. Ver la sección de lecturas adicionales abajo para las ligas en internet.
11.7. ¿Qué hemos aprendido?
Haciendo un recuento de lo que hemos cubierto en esta hoja de ejercicios:
La interpolación utiliza puntos de vector con valores conocidos para estimar valores en ubicaciones desconocidas con el fin de crear una superficie ráster que cubra un área completa.
El resultado de la interpolación típicamente es una capa ráster.
Es importante Encontrar un método de interpolación adecuado para estimar de manera óptima valores para ubicaciones desconocidas.
La interpolación IDW asigna pesos a los puntos de muestra, tales que la influencia de un punto en otro decrece con la distancia hacia el nuevo punto que se está estimando.
La interpolación TIN utiliza puntos de muestra para crear una superficie formada por triángulos basada en información de los puntos vecinos más cercanos.
11.8. ¡Ahora a intentar!
Aquí hay algunas ideas para intentar con los alumnos:
El departamento de agricultura planea cultivar nuevas tierras en su área pero además de las características del suelo, ellos quieren saber si la lluvia es suficiente para una buena cosecha. Toda la información que tienen disponible viene de algunas pocas estaciones meteorológicas establecidas en el área. Crear una superficie interpolada con los alumnos que muestre qué áreas es probable que reciban mayor cantidad de lluvia.
La oficina de turismo desea publicar información acerca de la condiciones del clima en enero y febrero. Ellos tienen los datos de temperatura, lluvia y fuerza de los vientos y piden que se interpolen sus datos para estimar lugares en donde los turistas probablemente tendrán condiciones del clima óptimas con temperaturas medias, sin lluvia y poca fuerza del viento. ¿Se puede identificar las áreas en la región que cumplan estos criterios?
11.9. Algo en qué pensar.
Si no se tiene una computadora disponible, se puede utilizar una carta topográfica y una regla para estimar valores de elevación entre líneas de contorno o valores de lluvia entre estaciones meteorológicas ficticias. Por ejemplo, si la lluvia en la estación meteorológica A es de 50 mm por mes y en la estación meteorológica B es de 90 mm, se puede estimar que la lluvia a la mitad de la distancia entre las estaciones A y B es de 70 mm.
11.10. Otras lecturas
Libros:
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
DeMers, Michael N. (2005): Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Mitas, L., Mitasova, H. (1999). Spatial Interpolation. In: P.Longley, M.F. Goodchild, D.J. Maguire, D.W.Rhind (Eds.), Geographical Information Systems: Principles, Techniques, Management and Applications, Wiley.
Sitios web:
La guía del usuario de QGIS también tiene más información detallada sobre las herramientas de interpolación proporcionadas en QGIS.
11.11. ¿Qué sigue?
Esta es la hoja de ejercicios final en esta serie. ¡Le animamos a que explore QGIS y utilice el manual de QGIS que lo acompaña para descubrir todas las otras cosas que se pueden realizar con el software SIG!
