Coördinaten ReferentieSysteem¶

Overzicht¶

Map projections try to portray the surface of the earth or a portion of the earth on a flat piece of paper or computer screen. A coordinate reference system (CRS) then defines, with the help of coordinates, how the two-dimensional, projected map in your GIS is related to real places on the earth. The decision as to which map projection and coordinate reference system to use, depends on the regional extent of the area you want to work in, on the analysis you want to do and often on the availability of data.

Kaartprojectie in detail¶

Een traditionele methode voor het weergeven van de vorm van de aarde is het gebruiken van wereldbollen. Er is echter een probleem met die benadering. Hoewel wereldbollen het grootste gedeelte van de vorm van de aarde behouden en de ruimtelijke configuratie van continent-grote objecten, zijn zij moeilijk mee te nemen in uw broekzak. Zij zijn ook alleen handig om te gebruiken op extreem kleine schalen (bijv. 1:100 miljoen).

De meeste gegevens voor thematische kaarten die veelal worden gebruikt in toepassingen voor GIS zijn van een aanmerkelijk grotere schaal. Typische gegevenssets voor GIS hebben schalen van 1:250 000 of groter, afhankelijk van het niveau van de details. Een wereldbol van deze grootte zou moeilijk een kostbaar te produceren zijn en zelfs moeilijker mee te nemen te zijn. Als resultaat daarvan hebben cartografen een verzameling technieken ontwikkeld, genaamd kaartprojecties, die zijn ontworpen om, met redelijke nauwkeurigheid, de bolvormige aarde in twee dimensies weer te geven.

Wanneer op korte afstand bekeken lijkt de aarde relatief vlak te zijn. Echter, bekeken vanuit de ruimte, kunnen we zien dat de aarde relatief bolvormig is. Kaarten, zoals we zullen zien in het komende onderwerp over het maken van kaarten, zijn vertegenwoordigingen van de realiteit. Zijn zijn niet alleen ontworpen om objecten weer te geven, maar ook hun vorm en ruimtelijke schikking. Elke kaartprojectie heeft voordelen en nadelen. De beste projectie voor een kaart is afhankelijk van de schaal van de kaart, en van de doelen waarvoor het zal worden gebruikt. Een projectie mag bijvoorbeeld onacceptabele vervormingen hebben als hij wordt gebruikt om het gehele continent Afrika in beeld te brengen, maar zou een excellente keus kunnen zijn voor een (gedetailleerde) kaart op grote schaal van uw land. De eigenschappen van een kaartprojectie zouden ook enige mogelijkheden voor het ontwerpen van de kaart kunnen beïnvloeden. Sommige projecties zijn goed voor kleine gebieden, sommige zijn goed voor het in kaart brengen van gebieden met een groot bereik van West naar Oost, en sommige zijn beter voor het in kaart brengen van gebieden met een groot bereik van Noord naar Zuid.

De drie families van kaartprojecties¶

The process of creating map projections can be visualised by positioning a light source inside a transparent globe on which opaque earth features are placed. Then project the feature outlines onto a two-dimensional flat piece of paper. Different ways of projecting can be produced by surrounding the globe in a cylindrical fashion, as a cone, or even as a flat surface. Each of these methods produces what is called a map projection family. Therefore, there is a family of planar projections, a family of cylindrical projections, and another called conical projections (see figure_projection_families)

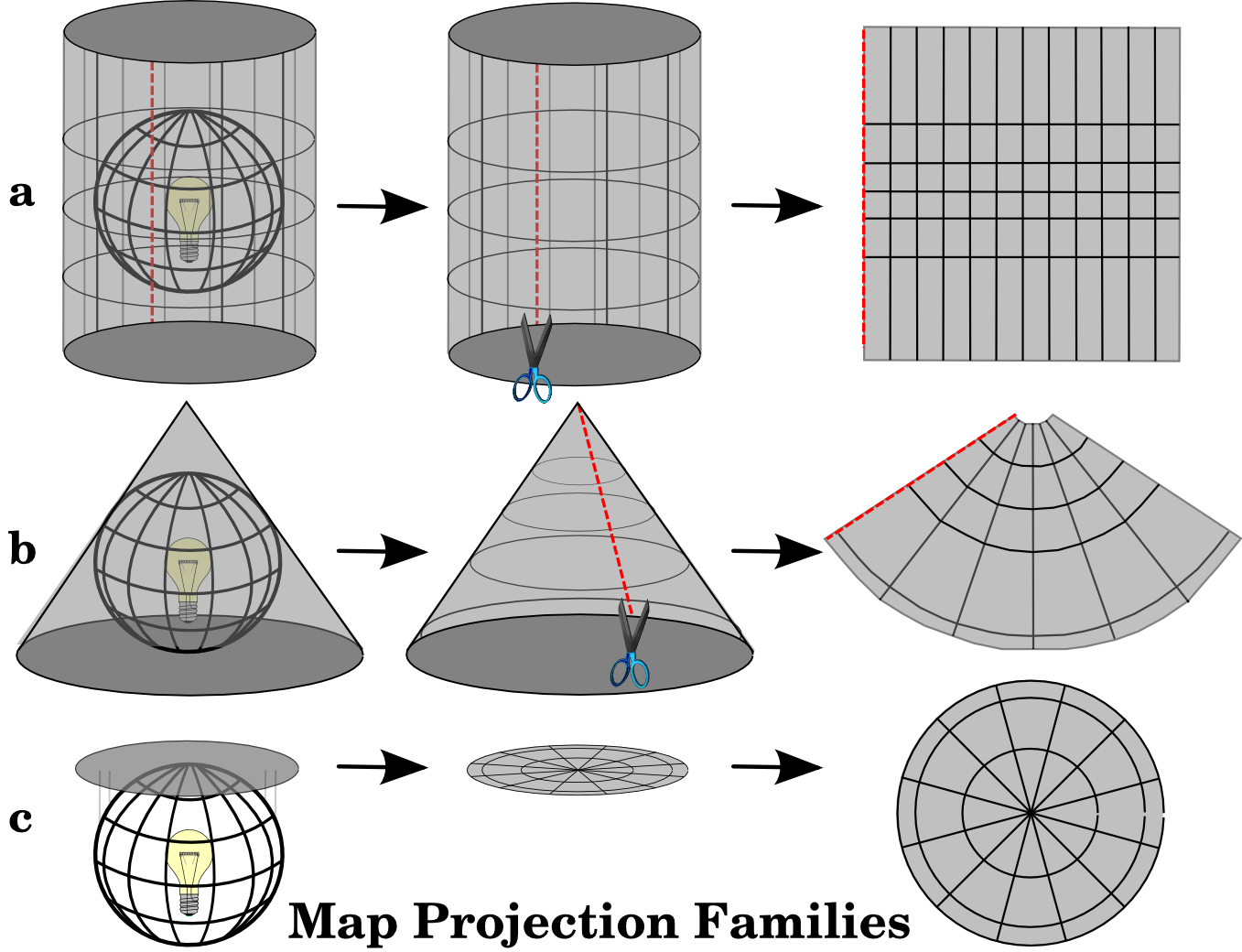
De drie families van kaartprojecties. Zij kunnen worden weergegeven als a) cilindrische projecties, b) kegelvormige projecties of c) vlakke projecties.

Heden ten dage wordt, natuurlijk,, het proces van het projecteren van de bolvormige aarde op een vlak stuk papier gedaan met behulp van de rekenkundige principes van geometrie en trigonometrie. Dit bootst de fysieke projectie van licht door de wereldbol na.

Nauwkeurigheid van kaartprojecties¶

Map projections are never absolutely accurate representations of the spherical earth. As a result of the map projection process, every map shows distortions of angular conformity, distance and area. A map projection may combine several of these characteristics, or may be a compromise that distorts all the properties of area, distance and angular conformity, within some acceptable limit. Examples of compromise projections are the Winkel Tripel projection and the Robinson projection (see figure_robinson_projection), which are often used for world maps.

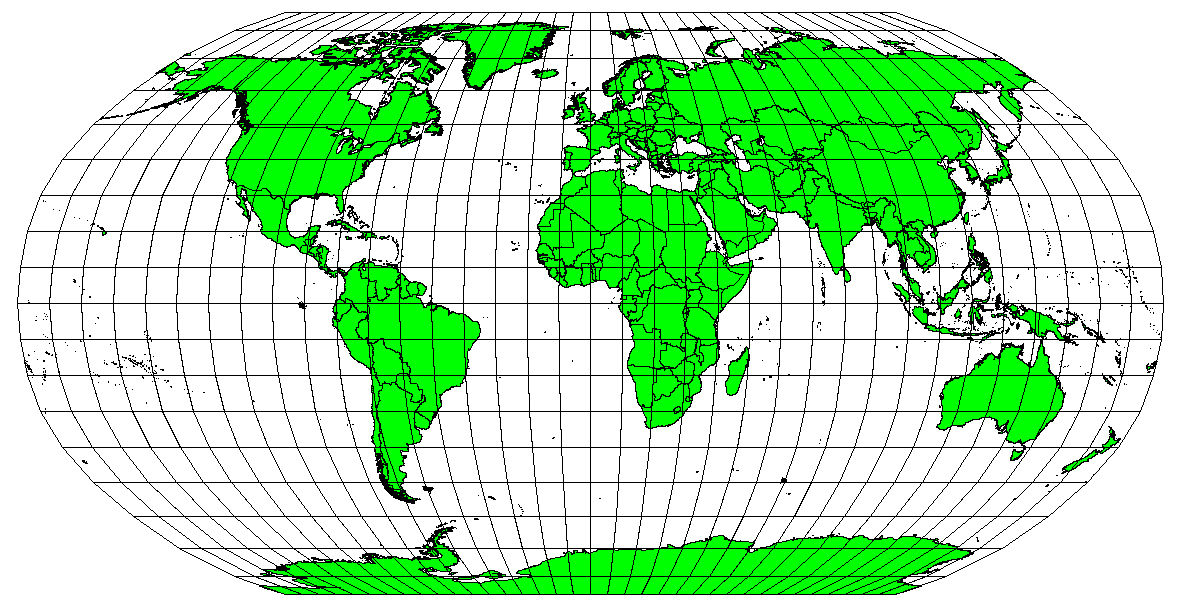
De Robinson-projectie is een compromis waar vervormingen van gebied, conformiteit van hoeken en afstand acceptabel zijn.

Het is normaal gesproken onmogelijk om tegelijkertijd alle karakteristieken in een kaartprojectie te behouden. Dit betekent dat wanneer u nauwkeurige analytische bewerkingen wilt uitvoeren, u een kaartprojectie moet gebruiken die de beste karakteristieken voor uw analyses verschaft. Als u bijvoorbeeld afstanden wilt meten op uw kaart, zou u moeten proberen een kaartprojectie voor uw gegevens te gebruiken die hoge nauwkeurigheid voor afstanden verschaft.

Conforme projecties (hoekgetrouw/gelijkvormig)¶

Bij het werken met een wereldbol zullen de hoofdrichtingen voor de kompasroos (Noord, Oost, Zuid en West) altijd 90 graden ten opzichte van elkaar staan. Met andere woorden: Oost staat altijd in een hoek van 90 graden ten opzichte van Noord. Onderhouden van de juiste eigenschappen voor hoeken kan ook in een kaartprojectie worden behouden. Een kaartprojectie die de eigenschap voor conformiteit van hoeken behoudt wordt een conforme of hoekgetrouwe projectie genoemd.

Deze projecties worden gebruikt wanneer het behouden van relaties van hoeken belangrijk is. Zij worden veelvuldig gebruikt voor navigatie- of meteorologische taken. Het is belangrijk om te onthouden dat het onderhouden van echte hoeken op een kaart voor grote gebieden moeilijk is en zou alleen moeten worden geprobeerd op kleine gedeelten van de aarde. De conforme type projectie resulteert in vervormingen van gebieden, wat betekent dat, als er metingen werden verricht op de kaart, zij niet juist zullen zijn. Hoe groter het gebied hoe minde nauwkeurig de metingen van de gebieden zullen zijn. Voorbeelden zijn de Mercator-projectie (zoals weergegeven in figure_mercator_projection) en de Lambert Conformal Conic-projectie. De U.S. Geological Survey gebruikt een conforme projectie voor veel van zijn topografische kaarten.

De Mercator-projectie, bijvoorbeeld, wordt gebruikt waar relaties tussen hoeken belangrijk zijn, maar de relaties tussen gebieden zijn vervormd.

Equidistante projecties (afstandsgetrouw)¶

Als uw doel voor het projecteren van een kaart is om nauwkeurig afstanden te meten, zou u een projectie moeten selecteren die ontworpen is om afstanden goed te behouden. Dergelijke projecties, afstandsgetrouwe projecties genoemd, vereisen dat de schaal van de kaart constant wordt gehouden. Een kaart is afstandsgetrouw wanneer die op juiste wijze afstanden weergeeft vanaf het centrum van de projectie tot elke andere plaats op de kaart. Afstandsgetrouwe projecties onderhouden nauwkeurige afstanden vanuit het centrum van de projectie of langs opgegeven lijnen. Deze projecties worden gebruikt voor radiokaarten en seismische kaarten en voor navigatie. De Plate Carree Equidistant Cylindrical (zie figure_plate_caree_projection) en de Equirectangular-projectie zijn twee goede voorbeelden van equidistante (afstandsgetrouwe) projecties. De Azimuthal Equidistant projectie is de projectie die is gebruikt voor het embleem van de Verenigde Naties (zie figure_azimuthal_equidistant_projection).

De Plate Carree Equidistant Cylindrical-projectie, bijvoorbeeld, wordt gebruikt als nauwkeurig meten van afstanden belangrijk is.

Het logo van de Verenigde Naties gebruikt de Azimuthal Equidistant-projectie.

Equivalente projecties (oppervlaktegetrouw)¶

When a map portrays areas over the entire map, so that all mapped areas have the same proportional relationship to the areas on the Earth that they represent, the map is an equal area map. In practice, general reference and educational maps most often require the use of equal area projections. As the name implies, these maps are best used when calculations of area are the dominant calculations you will perform. If, for example, you are trying to analyse a particular area in your town to find out whether it is large enough for a new shopping mall, equal area projections are the best choice. On the one hand, the larger the area you are analysing, the more precise your area measures will be, if you use an equal area projection rather than another type. On the other hand, an equal area projection results in** distortions of angular conformity** when dealing with large areas. Small areas will be far less prone to having their angles distorted when you use an equal area projection. Alber’s equal area, Lambert’s equal area and Mollweide Equal Area Cylindrical projections (shown in figure_mollweide_equal_area_projection) are types of equal area projections that are often encountered in GIS work.

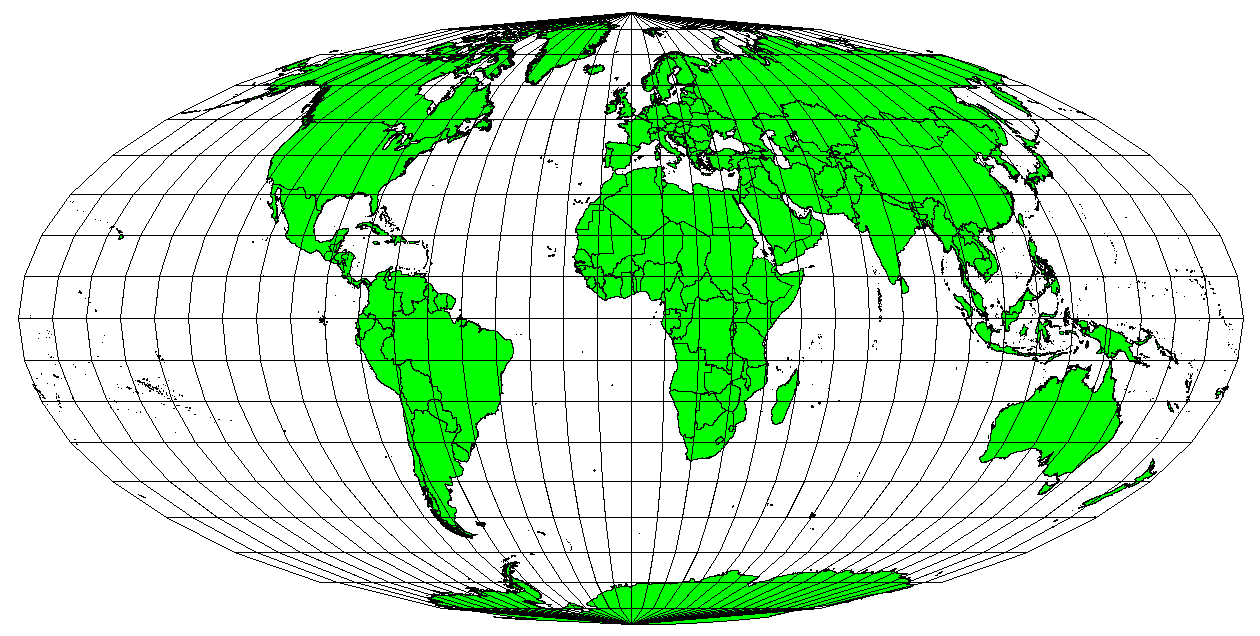
De Mollweide Equal Area Cylindrical-projectie, bijvoorbeeld, zorgt er voor dat alle in kaart gebrachte gebieden dezelfde proportionele relatie tot de gebieden op Aarde hebben.

Onthoud dat kaartprojectie een zeer complex onderwerp is. Er zijn honderden verschillende projecties wereldwijd beschikbaar, die elk proberen een bepaald gedeelte van de oppervlakte van de Aarde zo waarheidsgetrouw mogelijk weer te geven op een vlak stuk papier. In de echte wereld zal de keuze over welke projectie wordt gebruikt, al vaak voor u genomen zijn. De meeste landen hebben algemeen gebruikte projecties en wanneer gegevens worden uitgewisseld volgen mensen de nationale trend.

Coördinaten ReferentieSysteem (CRS) in detail¶

Met behulp van coördinaten referentiesystemen (CRS) kan elke plaats op aarde worden gespecificeerd door een set van drie getallen, coördinaten genaamd. In het algemeen kunnen CRS-en worden opgedeeld in geprojecteerde coördinaten referentiesystemen (ook wel Cartesiaanse of rechthoekige coördinaten referentiesystemen genoemd) en geografische coördinaten referentiesystemen.

Geografische coördinatensystemen¶

Het gebruiken van Geografische Coördinaten ReferentieSystemen komt veel voor. Zij gebruiken graden van breedte- en lengtegraad en soms ook een waarde voor de hoogte om een locatie op het oppervlak van de aarde te beschrijven. De meest populaire is genaamd WGS 84.

Breedtegraden lopen parallel aan de evenaar en verdelen de aarde in 180 gelijk delen van dezelfde grootte van Noord naar Zuid (of van Zuid naar Noord). De verwijzing voor de breedtegraden is de evenaar en elke hemisfeer is verdeeld in negentig gedeelten, die elk één breedtegraad weergeven. In de noordelijke hemisfeer worden breedtegraden gemeten vanaf nul op de evenaar tot en met negentig op de Noordpool. In de zuidelijke hemisfeer worden breedtegraden gemeten vanaf nul op de evenaar tot en met negentig op de Zuidpool. Breedtegraden in de zuidelijk hemisfeer worden vaak negatieve waarden toegekend (0 tot en met -90°) om het digitaliseren van kaarten te vereenvoudigen. Waar u zich ook op het oppervlak van de aarde bevindt, de afstand tussen de breedtegraden is hetzelfde (60 nautische mijlen). Zie figure_geographic_crs voor een afbeelding.

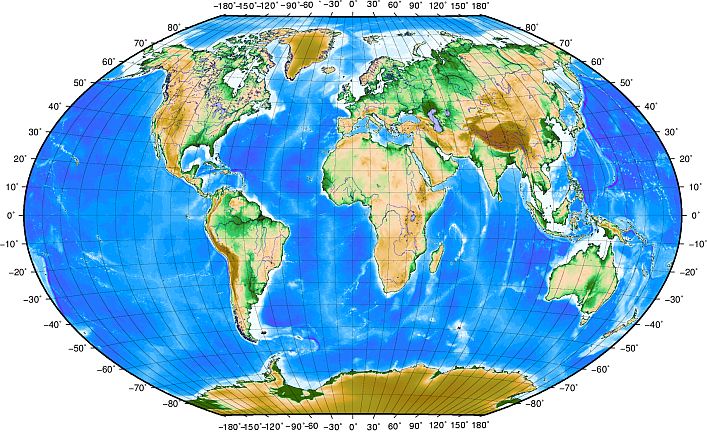
Geografisch coördinatensysteem met breedtegraden parallel aan de evenaar en lengtegraden met de primaire meridiaan door Greenwich.

Lengtegraden, aan de andere kant, voldoen niet zo goed aan de standaard voor uniformiteit. Lengtegraden lopen loodrecht aan de evenaar en convergeren aan de polen. De lengtegraad voor verwijzing (de primaire meridiaan) loopt vanaf de Noordpool naar de Zuidpool door Greenwich, Engeland. Opeenvolgende lengtegraden worden gemeten van nul tot en met 180 graden van Oost naar West vanaf de primaire meridiaan. Onthoud dat waarden ten westen van de primaire meridiaan negatieve waarden krijgen toegewezen bij gebruik in toepassingen voor digitale kaarten. Zie figure_geographic_crs voor een afbeelding.

Op de evenaar, en alleen op de evenaar, is de afstand die wordt weergegeven door één lengtegraad gelijk aan de afstand die wordt weergegeven door één breedtegraad. Als u zich verplaatst naar de polen wordt de afstand tussen de lengtegraden progressief minder, totdat, op de exacte locatie van de pool, alle 360° lengtegraden worden weergegeven door één enkel punt waarop u uw vinger zou kunnen leggen (u zou daarbij toch waarschijnlijk handschoenen willen dragen). Met behulp van het geografische coördinatensysteem hebben we een raster van lijnen, die de aarde opdelen in vierkanten, die bij benadering 12363,365 vierkante kilometer op de evenaar bedekken — een goed begin, maar niet erg nuttig voor het bepalen van de locatie van iets binnen dat vierkant.

Een kaartraster moet, om echt nuttig te zijn, worden verdeeld in dusdanig kleine gedeelten dat zij kunnen worden gebruikt om (met een acceptabel niveau van nauwkeurigheid) de locatie van een punt op de kaart te beschrijven. Graden worden opgedeeld in minuten (') en seconden (") om dat te bereiken. Er zitten zestig minuten in een graad en zestig seconden in een minuut (3600 seconden in één graad). Dus, aan de evenaar, één seconde breedte- of lengtegraad = 30,87624 meters.

Geprojecteerde coördinaten referentiesystemen¶

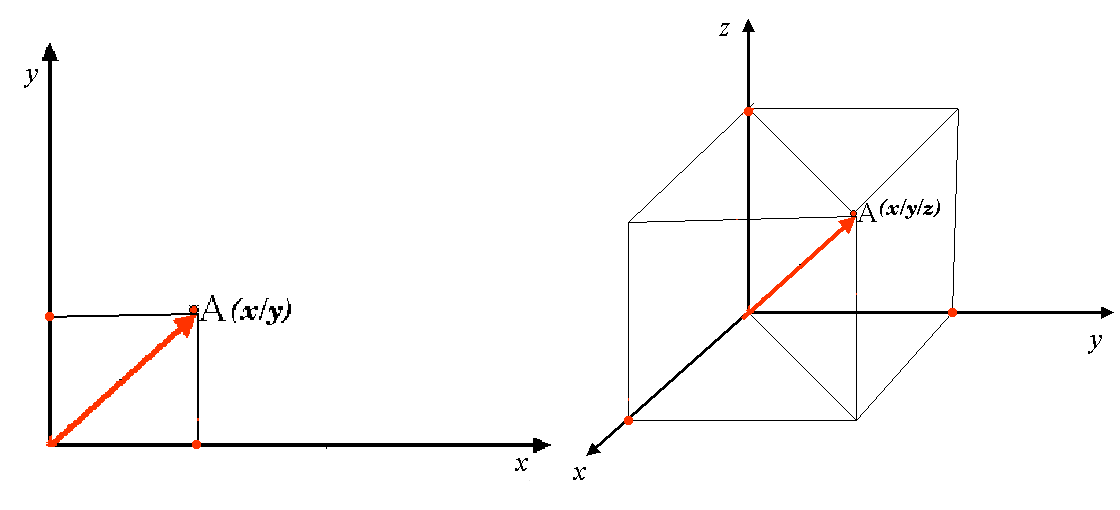
Een tweedimensionaal coördinaten referentiesysteem wordt in het algemeen gedefinieerd door twee assen. Met rechte hoeken ten opzichte van elkaar vormen zij een zogenaamd XY-vlak (zie figure_projected_crs aan de linkerkant). De horizontale as is normaal gesproken gelabeld X, en de verticale as is normaal gesproken gelabeld Y. In een driedimensionaal coördinaten referentiesysteem wordt een andere as, normaal gesproken gelabeld Z, toegevoegd. Die staat ook in een rechte hoek ten opzichte van de X- en Y-as. De Z-as verschaft de derde dimensie van ruimte (zie figure_projected_crs aan de rechterkant). Elk punt dat kan worden uitgedrukt in bolcoördinaten kan worden uitgedrukt als een X Y Z-coördinaat.

Twee- en driedimensionale coördinaten referentiesystemen.

Een geprojecteerd coördinaten referentiesysteem in de zuidelijke hemisfeer (ten zuiden van de evenaar) heeft normaal gesproken zijn origine op de evenaar op een specifieke lengtegraad. Dit betekent dat de waarden voor Y in zuidelijke richting verhogen en de waarden voor X in westelijke richting verhogen. In de noordelijke hemisfeer (ten noorden van de evenaar) s de origine ook op de evenaar op een specifieke lengtegraad. Echter, nu verhogen de waarden van Y in noordelijke richting en de waarden voor X verhogen in oostelijke richting. In het volgende gedeelte beschrijven we een geprojecteerd coórdinaten referentiesysteem, genaamd Universal Transverse Mercator (UTM) vaak gebruikt voor Zuid Afrika.

Universal Transverse Mercator (UTM) CRS in detail¶

Het Universal Transverse Mercator (UTM) coördinaten referentiesysteem vindt zijn origine op de evenaar op een specifieke lengtegraad. De waarden voor Y verhogen nu in zuidelijke richting en de waarden voor X verhogen in westelijke richting. Het CRS UTM is een globale kaartprojectie. Dit betekent dat het in het algemeen over de gehele wereld gebruikt wordt. Maar, zoals al eerder beschreven in het gedeelte ‘nauwkeurigheid van kaartprojecties’ hierboven, hoe groter het gebied (bijvoorbeeld Zuid-Afrika) hoe meer vervorming van de conformiteit van hoeken, afstand en gebied er optreedt. , De wereld is opgedeeld in 60 gelijke zones die allemaal 6 graden breed in lengte zijn van Oost naar West, om teveel vervorming te vermijden. De zones voor UTM zijn genummerd van 1 tot en met 60, beginnend op de internationale datumlijn (zone 1 op 180 graden Westerlengte) en doorlopend naar het Oosten terug naar de internationale datumlijn (zone 60 op 180 graden Oosterlengte) zoals weergegeven in figure_utm_zones.

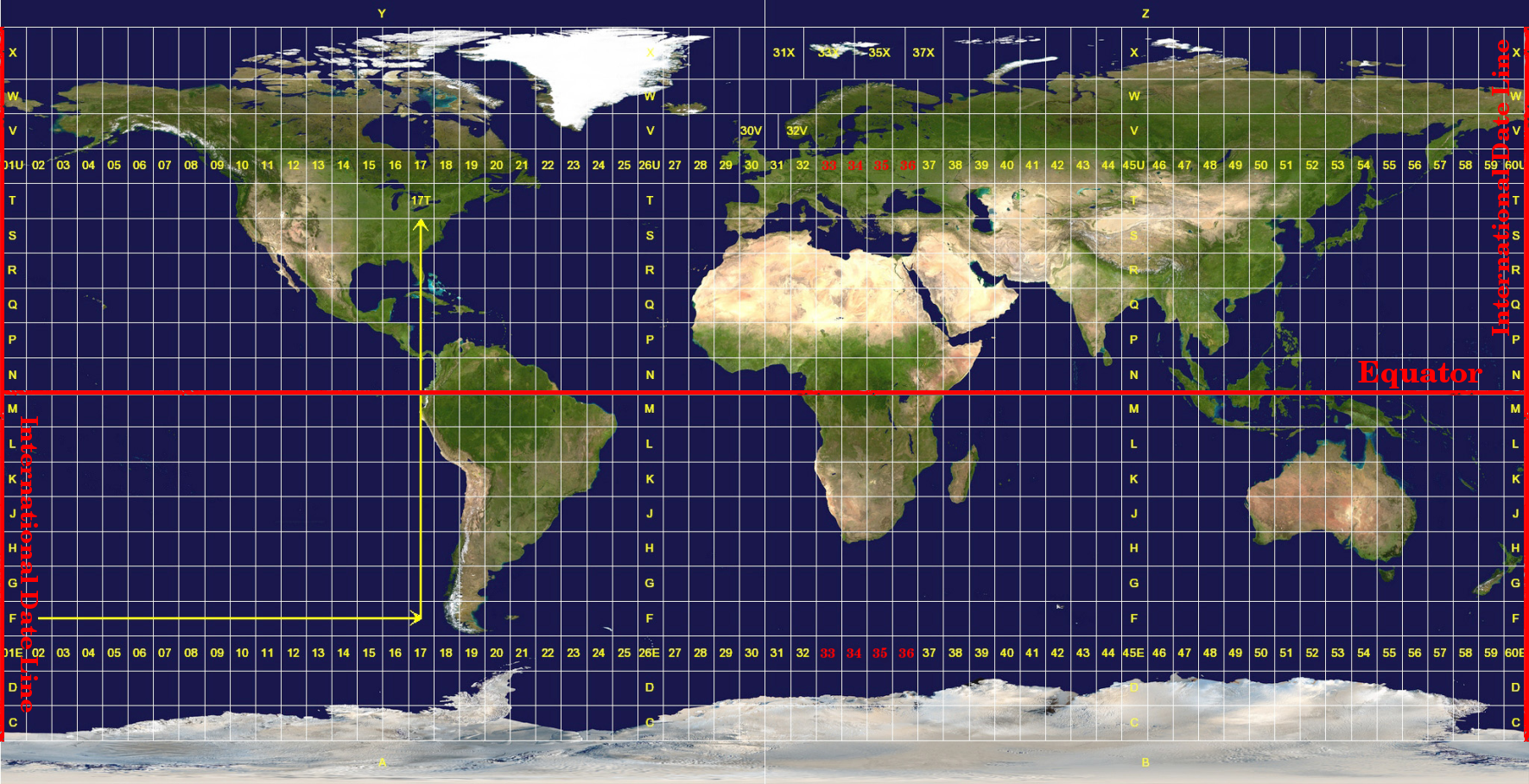
De zones voor Universal Transverse Mercator. Voor Zuid-Afrika worden de UTM-zones 33S, 34S, 35S, en 36S gebruikt.

Zoals u kunt zien in in figure_utm_zones en figure_utm_for_sa, Zuid-Afrika wordt bedekt door vier UTM-zones om vervorming te minimaliseren. De zones worden UTM 33S, UTM 34S, UTM 35S en UTM 36S genoemd. De S na de zone betekent dat de UTM-zones ten zuiden van de evenaar zijn gelegen.

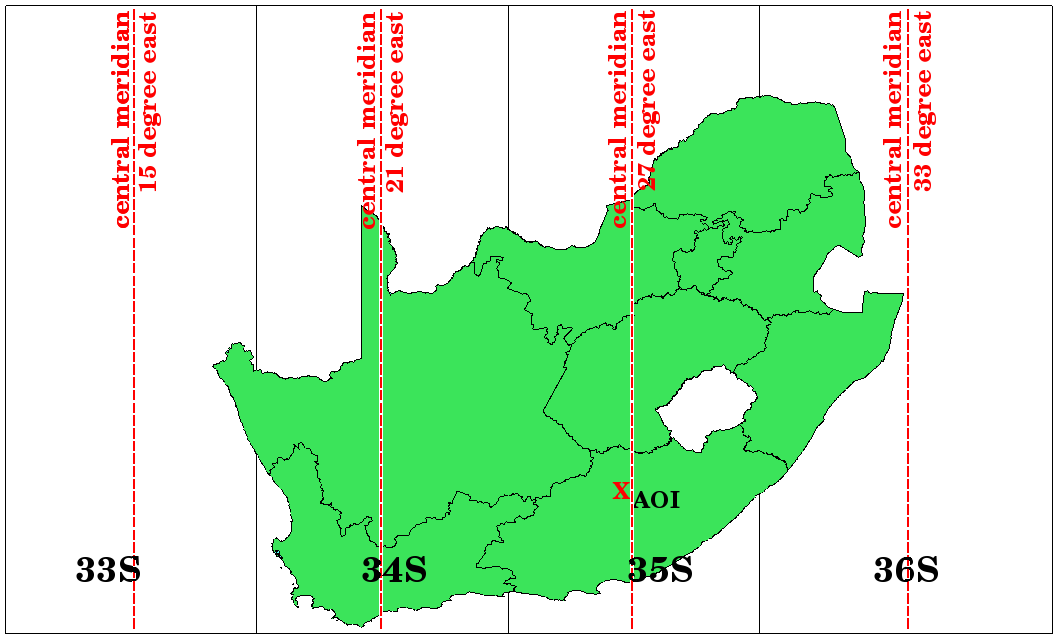
UTM-zones 33S, 34S, 35S en 36S met hun centrale lengtegraden (meridianen) gebruikt om Zuid-Afrika met grote nauwkeurigheid te projecteren. Het rode kruis geeft een Area of Interest (AOI) weer.

Stel, als voorbeeld, dat we een tweedimensionaal coördinaat willen definiëren binnen het Area of Interest (AOI) dat is gemarkeerd met een rood kruis in figure_utm_for_sa. U kunt zien dat het gebied is gelegen binnen de UTM-zone 35S. Dit betekent, om vervorming te minimaliseren en nauwkeurige analyseresultaten te verkrijgen, we UTM-zone 35S als het coördinaten referentiesysteem zouden moeten gebruiken.

The position of a coordinate in UTM south of the equator must be indicated with the zone number (35) and with its northing (y) value and easting (x) value in meters. The northing value is the distance of the position from the equator in meters. The easting value is the distance from the central meridian (longitude) of the used UTM zone. For UTM zone 35S it is 27 degrees East as shown in figure_utm_for_sa. Furthermore, because we are south of the equator and negative values are not allowed in the UTM coordinate reference system, we have to add a so called false northing value of 10,000,000 m to the northing (y) value and a false easting value of 500,000 m to the easting (x) value. This sounds difficult, so, we will do an example that shows you how to find the correct UTM 35S coordinate for the Area of Interest.

Gelijktijdige CRS-transformatie gebruiken¶

Zoals u zich waarschijnlijk kunt voorstellen zou er een situatie kunnen zijn waarbij de gegevens die u in een GIS wilt gebruiken zijn geprojecteerd in verschillende coördinaten referentiesystemen. U zou, bijvoorbeeld, een vectorlaag kunnen krijgen die de grenzen van Zuid-Afrika geprojecteerd in UTM 35S weergeeft en een andere vectorlaag met punt-informatie over de regenval die is verschaft in het geografische coördinatensysteem WGS 84. In GIS worden deze twee vectorlagen in twee totaal verschillende delen van het kaartvenster geplaatst, omdat zij verschillende projecties hebben.

Om dit probleem op te lossen bevatten veel GIS systemen functionaliteit om on-the-fly projecties te transformeren. De projectie die actief is bij het starten van de applicatie bepaalt in welke projectie lagen die worden geladen worden weergegeven. Hierdoor kunnen lagen en bronnen in verschillende projecties toch in hetzelfde venster worden weergegeven. De projectie waarin lagen worden geladen kan worden gewijzigd door de projectie van het project te wijzigen via het instellingen menu.

Algemene problemen / dingen om te onthouden¶

Het onderwerp kaartprojectie is bijzonder complex en zelfs professionals die geografie, geomatics of een andere aan GIS gerelateerde wetenschap hebben gestudeerd, hebben vaak problemen met de juiste definitie van kaartprojecties en coördinaten referentiesystemen. Normaal gesproken, wanneer u met GIS werkt, heeft u al geprojecteerde gegevens om mee te beginnen. In de meeste gevallen zullen die gegevens zijn geprojecteerd in een bepaald CRS, dus hoeft u geen nieuw CRS te maken of zelfs niet de gegevens van het ene CRS naar het andere opnieuw te projecteren. Dat gezegd hebbende is het altijd handig een idee te hebben van war kaartprojectie en CRS betekenen.

Wat hebben we geleerd?¶

Laten we eens samenvatten wat er in dit gedeelte besproken is:

• Kaartprojecties portretteren de oppervlakte van de aarde op een tweedimensionaal, vlak stuk papier of computerscherm.

• Er zijn globale kaartprojecties, maar de meeste kaartprojecties worden gemaakt en geoptimaliseerd om kleinere gebieden te projecteren van het oppervlakte van de aarde.

• Kaartprojecties zijn nooit absoluut nauwkeurige weergaven van de bolvormige aarde. Zij geven vervormingen van de conformiteit van hoeken, afstand en gebied weer. Het is onmogelijk om al deze karakteristieken tegelijkertijd in een kaartprojectie te behouden.

• Een Coördinaten referentiesysteem (CRS) definieert, met behulp van coördinaten, hoe de tweedimensionale, geprojecteerde kaart is gerelateerd aan echte locaties op aarde.

• er zijn twee verschillende typen coördinaten referentiesystemen: Geografische coördinatensystemen en Geprojecteerde coördinatensystemen.

• Directe projectie is een functionaliteit in GIS die ons in staat stelt lagen over elkaar hen te leggen, zelfs als zijn zijn geprojecteerd in verschillende coördinaten referentiesystemen.

Nu zelf aan de slag!¶

Hier zijn enkele ideeën die u kunt proberen met uw leerlingen:

• Start QGIS en laad twee lagen van hetzelfde gebied maar met verschillende projecties en laat uw leerlingen de coördinaten zoeken van verscheidene plaatsen op de twee lagen. U kunt ze late zien dat het niet mogelijk is de twee lagen over elkaar heen te leggen. Definieer dan het coördinaten referentiesysteem als geografisch/WGS 84 in het dialoogvenster Projectinstellingen en activeer het keuzevak Gelijktijdige CRS-transformatie gebruiken. Laad de twee lagen van hetzelfde gebied opnieuw en laat uw leerlingen zien hoe Gelijktijdige CRS-transformatie gebruiken werkt.

• U kunt het dialoogvenster Projectinstellingen in QGIS openen en laat uw leerlingen de vele verschillende Coördinaten ReferentieSystemen zien, zodat zij een idee van de complexiteit van dit onderwerp krijgen. Met ‘Gelijktijdige CRS-transformatie gebruiken’ ingeschakeld kunt u verschillende CRS-en selecteren om dezelfde laag in verschillende projecties te laten zien.

Iets om over na te denken¶

If you don’t have a computer available, you can show your pupils the principles of the three map projection families. Get a globe and paper and demonstrate how cylindrical, conical and planar projections work in general. With the help of a transparency sheet you can draw a two-dimensional coordinate reference system showing X axes and Y axes. Then, let your pupils define coordinates (x and y values) for different places.

Meer informatie¶

Boeken:

• Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
• DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
• Galati, Stephen R. (2006): Geographic Information Systems Demystified. Artech House Inc. ISBN: 158053533X

Websites:

• http://www.colorado.edu/geography/gcraft/notes/mapproj/mapproj_f.html
• http://geology.isu.edu/geostac/Field_Exercise/topomaps/index.htm

De QGIS User Guide heeft ook meer gedetailleerde informatie over het werken met kaartprojecties in QGIS.

Hoe verder?¶

In het volgende gedeelte zullen we Het maken van kaarten nader gaan bekijken.