Topologia¶

Panoramica¶

La topologia esprime le relazioni spaziali tra le geometrie vettoriali (punti, polilinee e poligoni) collegate o adiacenti in un GIS. I dati topologici sono utili per individuare e correggere gli errori di digitalizzazione (ad esempio, due line in un vettore di strade che non si incontrano perfettamente a un incrocio). La topologia è necessaria per effettuare alcuni tipi di analisi spaziale, come l’analisi di reti.

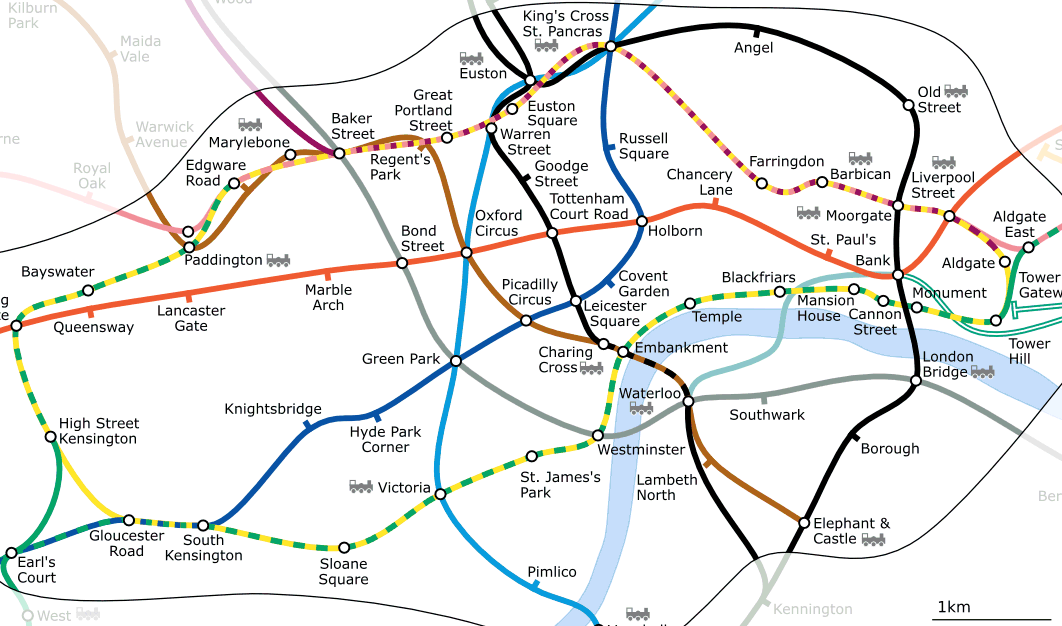
Immagina di andare a Londra. Per un giro turistico hai intenzione di visitare la Cattedrale di St. Paul la mattina e nel pomeriggio il mercato di Covent Garden per comprare qualche souvenir. Guardando la mappa della metropolitana di Londra (vedi figure_topology_london) dovi trovare i treni che collegano Covent Garden a St. Paul. Ciò richiede informazioni topologiche (dati) di dove è possibile cambiare i treni. Guardando una mappa della metropolitana, le relazioni topologiche sono illustrate da cerchi che mostrano la connettività.

Topologia della rete metropolitana di Londra

Errori topologici¶

Ci sono diversi tipi di errori topologici e puoi raggrupparli a seconda che le geometrie vettoriali siano poligoni o polilinee. Errori topologici con poligoni possono includere poligoni non chiusi, spazi tra i bordi dei poligoni o confini sovrapposti. Un errore topologico comune con polilinee è quando non si incontrano perfettamente in un punto (nodo). Questo tipo di errore è chiamato difetto nel caso di un piccolo divario tra le linee, e eccesso se le linee terminano oltre il punto di incontro (vedi figure_topology_errors).

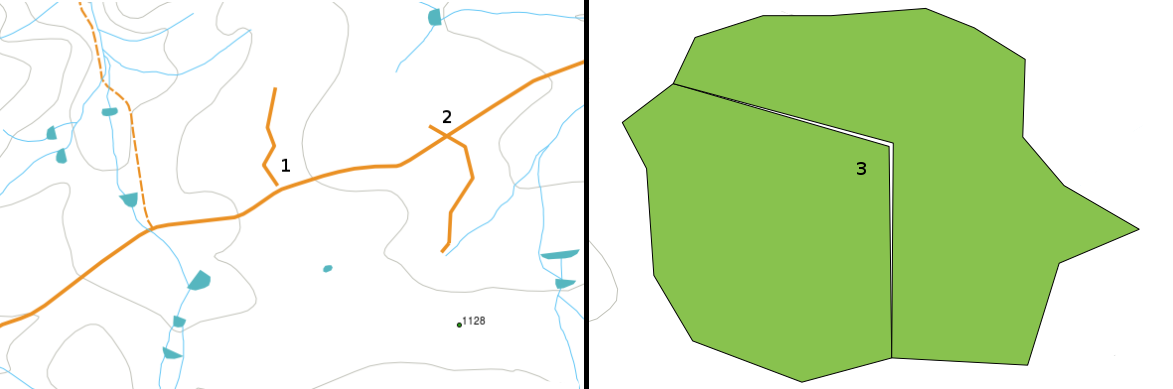
Il difetto (1) si verifica quando le linee vettoriali digitalizzate che dovrebbe essere collegate tra di loro non si toccano. L’eccesso (2) è quando una linea termina oltre la linea a cui dovrebbe connettersi. Lo sfasamento (3) si verifica quando i vertici di due poligoni non corrispondono ai loro confini.

Il risultato di errori di difetto e di eccesso sono i cosiddetti ‘nodi penzoloni’ all’estremità della linea. I nodi penzoloni sono accettabili in casi particolari, ad esempio se sono collegati a strade senza uscita.

Gli errori topologici interrompono le corrette relazioni tra le geometrie vettoriali. Questi errori devono essere sistemati per essere in grado di analizzare i dati vettoriali con procedure come analisi di reti (ad esempio trovare il percorso più breve in una rete stradale) o misure (ad esempio determinare la lunghezza di un fiume). Oltre al fatto che la topologia è utile per l’analisi di reti e per le misure, ci sono altri motivi per cui è importante e utile creare o avere dati vettoriali con topologia corretta. Immagina di digitalizzare i confini comunali della tua provincia e i poligoni si sovrappongono o presentano lacune. Se tali errori fossero presenti, non saresti in grado di utilizzare gli strumenti di misura e i risultati che otterresti non sarebbero corretti. Non sapresti la superficie corretta di ogni comune e non saresti in grado di definire esattamente dove sono i confini tra i comuni.

Avere dati topologicamente corretti, non è importante solo per le tue analisi, ma anche per le persone a cui passerai i dati: infatti si aspettano che i tuoi dati e le tue analisi risultino corretti!

Regole topologiche¶

Fortunatamente molti errori comuni che si fanno digitalizzando geometrie vettoriali possono essere prevenuti utilizzando regole topologiche implementate da molte applicazioni GIS

Fatta eccezione per alcuni formati speciali di dati GIS, la coerenza topologica di solito non è attivata come impostazione predefinita. Molti comuni GIS, come QGIS, definiscono la topologia come rapporti spaziali e lasciano all’utente la scelta di attivarle in un livello vettoriale.

L’elenco seguente mostra alcuni esempi di dove puoi applicare le proprietà topologiche di una mappa vettoriale per elementi del mondo reale:

• I confini comunali non devono sovrapporsi.

• I confini comunali non devono lasciare lacune (difetti).

• Le particelle di proprietà devono essere chiuse. Lacune o sovrapposizioni della linea di confine non è ammessa.

• Le linee di contorno in un vettore linee non devono intersecarsi (l’una nell’altra).

Strumenti topologici¶

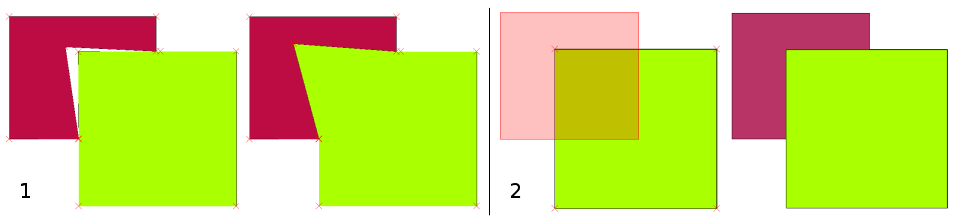
Molte applicazioni GIS forniscono strumenti per la validazione topologica. Per esempio in QGIS è possibile attivare Abilita la modifica topologica per migliorare la modifica e il mantenimento di confini comuni in layer di poligoni. Un GIS come QGIS ‘rileva’ un limite condiviso in una vettore poligoni così che devi spostare un solo vertice di confine di un poligono e QGIS assicurerà il mantenimento dei confini degli altri poligoni come mostrato in figure_topological_tools (1).

Un’altra opzione topologica consente di impedire la sovrapposizone di poligoni durante la digitalizzazione (vedi figure_topological_tools (2)). Se disponi già di un poligono, puoi con questa opzione digitalizzare un secondo poligono sovrapposto, QGIS taglierà il secondo poligono lasciando nel tratto sovrapposto il confine comune.

(1) Topological editing to detect shared boundaries, when moving vertices. When moving a vertex, all features that share that vertex are updated. (2) To avoid polygon overlaps, when a new polygon is digitised (shown in red) it is clipped to avoid overlapping neighbouring areas.

Distanza di “snapping”¶

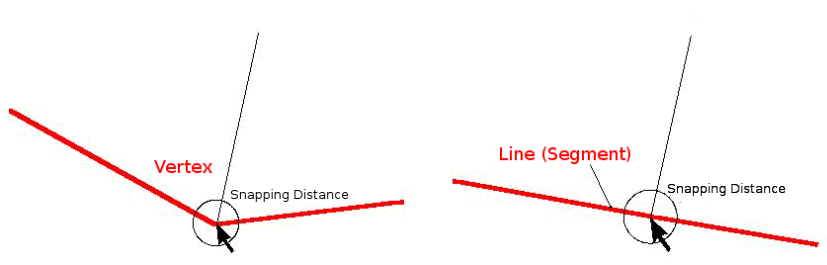
La distanza di aggancio è la distanza che un GIS utilizza per cercare il più vicino vertice e/o segmento che sta tentando di agganciarsi quando digitalizzi. Un segmento è una linea retta tra due vertici in un poligono o in una polilinea. Se non sei dentro la distanza di aggancio, un GIS come QGIS lascerà il vertice in cui clicchi il pulsante del mouse, invece di agganciarlo al vertice esistente e/o al segmento (vedi figure_snapping_distance).

La distanza di aggancio (circonferenza nera) è definito in unità di mappa (ad esempio gradi decimali) per agganciarsi ai vertici o ai segmenti.

Raggio di ricerca¶

Il raggio di ricerca è la distanza che un GIS utilizza per cercare il più vicino vertice che si sta tentando di agganciare. Se non sei all’interno del raggio di ricerca, il GIS no troverà nessun vertice. In linea di principio, è molto simile alla funzionalità distanza di aggancio.

La distanza di snap e il raggio di ricerca sono entrambi impostati in unità di mappa quindi potrebbe essere necessario provare per ottenere il valore della distanzagiusto. Se specifichi un valore troppo grande, il GIS può scattare per un vertice sbagliato, soprattutto se hai a che fare con un gran numero di vertici vicini. Se specifichi il raggio di ricerca troppo piccolo l’applicazione GIS non troverà nessun elemento o vertice da agganciare.

Problemi comuni / cose di cui essere consapevoli¶

E’ progettato per la semplicità e per la visualizzazione veloce, ma non per l’analisi dati che richiedono la topologia (come trovare percorsi in una una rete). Molte applicazioni GIS sono in grado di mostrare insieme elementi geometrici e topologici e alcune possono crearne, modificarli e analizzarli.

Cosa abbiamo imparato ?¶

Cerchiamo di riassumere gli argomenti che abbiamo affrontato in questo foglio di lavoro:

• La topologia mostra la relazione spaziale di elementi vettoriali vicini.

• Strumenti topologici gestiscono la topologia nel GIS

• Puoi usare la topologia per rilevare e correggere gli errori.

• Per alcuni strumenti, come l’analisi delle reti, la topologia è essenziale.

• La distanza di aggancio e il raggio di ricerca aiutano a digitare in modo topologicamente corretto i dati vettoriali.

• Il dato di geometria semplice non è necessariamente un dato topologicamente valido ma è comunemente usato nelle applicazioni GIS.

Adesso prova tu!¶

Ecco alcune idee per provare con i vostri studenti:

• Segna le fermate del tuo autobus locale su una mappa toposheet e richiedi ai tuoi allievi di trovare il percorso più breve tra due fermate.

• Pensa a come creeresti vettoriali in un GIS per rappresentare una rete stradale topologica della tua città. Quali regole topologiche sono importanti e quali strumenti possono usare i tuoi studenti in QGIS per fare in modo che il nuovo vettore strada sia topologicamente corretto?

Qualcosa su cui pensare¶

Se non disponi di un computer, puoi usare una mappa di una rete di autobus o ferroviaria e discutere le relazioni spaziali e la topologia con i tuoi studenti.

Altre letture¶

Libri

• Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
• DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195

Siti web:

• http://www.innovativegis.com/basis/primer/concepts.html
• http://en.wikipedia.org/wiki/Geospatial_topology

La guida dell’utente di QGIS fornisce anche infromazioni più dettagliate sull’editing topologico in QGIS

Cosa viene adesso?¶

Nel prossima sezione daremo un’occhiata più da vicino ai Sistemi di RIferimento per vedere come relazionare i dati dalla superficie terrestre sferica su una mappa piana