Топология¶
 |
Цели: |
Разбиране на топологията за векторни данни |
Ключови думи: |
Вектори, топология, топологични правила, топлогични грешки, радиус на търсене, разтояние за привързване, проста единица |
Преглед¶
Topology expresses the spatial relationships between connecting or adjacent vector features (points, polylines and polygons) in a GIS. Topological or topology-based data are useful for detecting and correcting digitising errors (e.g. two lines in a roads vector layer that do not meet perfectly at an intersection). Topology is necessary for carrying out some types of spatial analysis, such as network analysis.
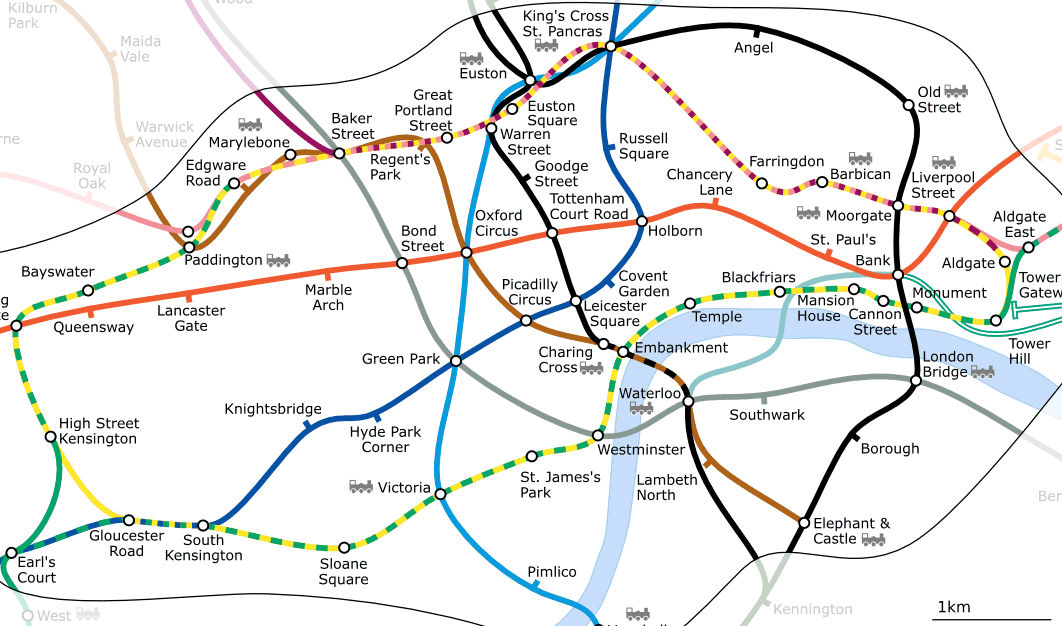
Imagine you travel to London. On a sightseeing tour you plan to visit St. Paul’s Cathedral first and in the afternoon Covent Garden Market for some souvenirs. Looking at the Underground map of London (see figure_topology_london) you have to find connecting trains to get from Covent Garden to St. Paul’s. This requires topological information (data) about where it is possible to change trains. Looking at a map of the underground, the topological relationships are illustrated by circles that show connectivity.
Топологични грешки¶
There are different types of topological errors and they can be grouped according to whether the vector feature types are polygons or polylines. Topological errors with polygon features can include unclosed polygons, gaps between polygon borders or overlapping polygon borders. A common topological error with polyline features is that they do not meet perfectly at a point (node). This type of error is called an undershoot if a gap exists between the lines, and an overshoot if a line ends beyond the line it should connect to (see figure_topology_errors).
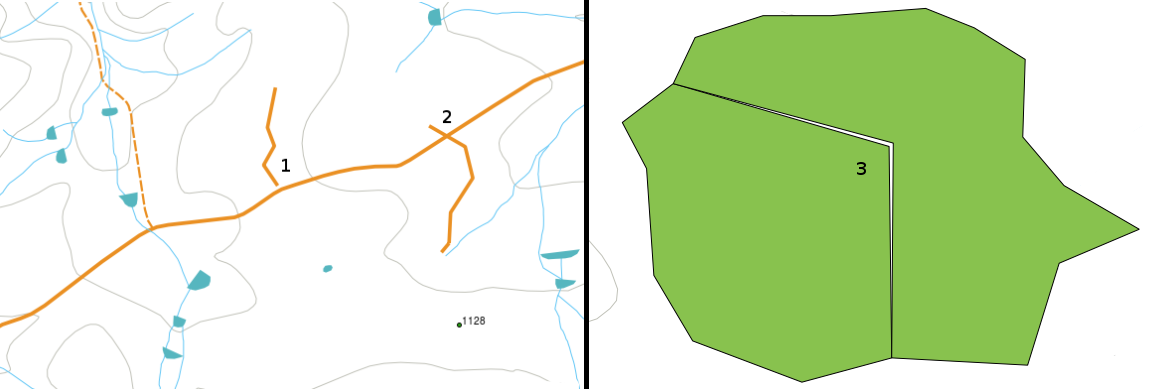
Undershoots (1) occur when digitised vector lines that should connect to each other don’t quite touch. Overshoots (2) happen if a line ends beyond the line it should connect to. Slivers (3) occur when the vertices of two polygons do not match up on their borders.
The result of overshoot and undershoot errors are so-called ‘dangling nodes’ at the end of the lines. Dangling nodes are acceptable in special cases, for example if they are attached to dead-end streets.
Topological errors break the relationship between features. These errors need to be fixed in order to be able to analyse vector data with procedures like network analysis (e.g. finding the best route across a road network) or measurement (e.g. finding out the length of a river). In addition to topology being useful for network analysis and measurement, there are other reasons why it is important and useful to create or have vector data with correct topology. Just imagine you digitise a municipal boundaries map for your province and the polygons overlap or show slivers. If such errors were present, you would be able to use the measurement tools, but the results you get will be incorrect. You will not know the correct area for any municipality and you will not be able to define exactly, where the borders between the municipalities are.
It is not only important for your own analysis to create and have topologically correct data, but also for people who you pass data on to. They will be expecting your data and analysis results to be correct!
Топологични прявила¶
Fortunately, many common errors that can occur when digitising vector features can be prevented by topology rules that are implemented in many GIS applications.
Except for some special GIS data formats, topology is usually not enforced by default. Many common GIS, like QGIS, define topology as relationship rules and let the user choose the rules, if any, to be implemented in a vector layer.
The following list shows some examples of where topology rules can be defined for real world features in a vector map:
- Area edges of a municipality map must not overlap.
- Area edges of a municipality map must not have gaps (slivers).
- Polygons showing property boundaries must be closed. Undershoots or overshoots of the border lines are not allowed.
- Contour lines in a vector line layer must not intersect (cross each other).
Топологични инструменти¶
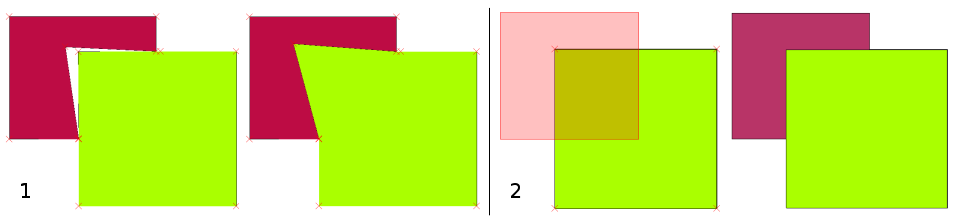
Many GIS applications provide tools for topological editing. For example in QGIS you can enable topological editing to improve editing and maintaining common boundaries in polygon layers. A GIS such as QGIS ‘detects’ a shared boundary in a polygon map so you only have to move the edge vertex of one polygon boundary and QGIS will ensure the updating of the other polygon boundaries as shown in figure_topological_tools (1).
Another topological option allows you to prevent** polygon overlaps** during digitising (see figure_topological_tools (2)). If you already have one polygon, it is possible with this option to digitise a second adjacent polygon so that both polygons overlap and QGIS then clips the second polygon to the common boundary.
Разстояние за допустимост на прилепване¶
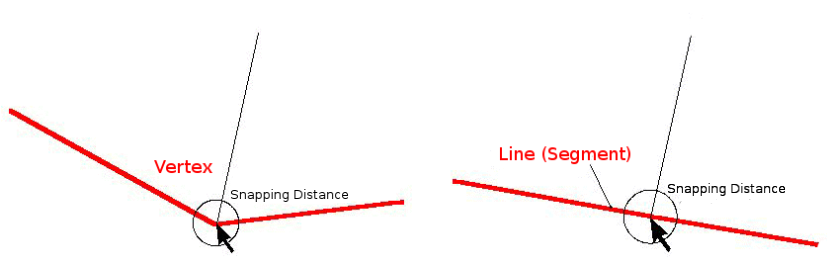
Snapping distance is the distance a GIS uses to search for the closest vertex and / or segment you are trying to connect when you digitise. A segment is a straight line formed between two vertices in a polygon or polyline geometry. If you aren’t within the snapping distance, a GIS such as QGIS will leave the vertex where you release the mouse button, instead of snapping it to an existing vertex and / or segment (see figure_snapping_distance).
Радиус на търсене¶
Search radius is the distance a GIS uses to search for the closest vertex you are trying to move when you click on the map. If you aren’t within the search radius, the GIS won’t find and select any vertex of a feature for editing. In principle, it is quite similar to the snapping distance functionality.
Snapping distance and search radius are both set in map units so you may need to experiment to get the distance value set right. If you specify a value that is too big, the GIS may snap to a wrong vertex, especially if you are dealing with a large number of vertices close together. If you specify the search radius too small the GIS application won’t find any feature or vertex to move or edit.
Common problems / things to be aware of¶
Mainly designed for simplicity and for fast rendering but not for data analysis that require topology (such as finding routes across a network). Many GIS applications are able to show topological and simple feature data together and some can also create, edit and analyse both.
Какво научихме?¶
Да обобщим какво покрихме с този работен лист:
Topology показва пространствената връзка на съседни векторни елементи.
Топологията в GIS е осигурена от topological tools.
Топологията може да се използва за да открием и поправим грешки пр цифроване.
За някои инструменти като мрежови анализ, топологично верните данни са ключови.
- Snapping distance and search radius help us to digitise topologically correct vector data.
- Simple feature data is not a true topological data format but it is commonly used by GIS applications.
Сега вие опитайте!¶
Here are some ideas for you to try with your learners:
- Mark your local bus stops on a toposheet map and then task your learners to find the shortest route between two stops.
- Think of how you would create vector features in a GIS to represent a topological road network of your town. What topological rules are important and what tools can your learners use in QGIS to make sure that the new road layer is topologically correct?
Something to think about¶
If you don’t have a computer available, you can use a map of a bus or railway network and discuss the spatial relationships and topology with your learners.
За следващо четене¶
Книги:
Chang, Kang-Tsung (2006). Introduction to Geographic Information Systems. 3rd Edition. McGraw Hill. ISBN: 0070658986
- DeMers, Michael N. (2005). Fundamentals of Geographic Information Systems. 3rd Edition. Wiley. ISBN: 9814126195
Сайтове:
- http://www.innovativegis.com/basis/primer/concepts.html
- http://en.wikipedia.org/wiki/Geospatial_topology
Ръководството за QGIS има по-детайлна информация за топогравското редактирано осигурено в QGIS.
Какво следва?¶
В секцията, която следва ще разгледаме Координатни системи за да разберем как са свързани данните от сферична земна форма към плоска карта!